34 (384)

86 JI. Parametryczne testy istotności

podobieństwo zdarzenia określonego taką właśnie nierównością. OtrzymiM jemy xl = 19,675. Z porównania obliczonej wartości^² z wartością krytyczni j xl wynika, że#²=16,5 < 19,675 =#². Ponieważ nie znaleźliśmy się w obsząfl rze krytycznym, zatem nie ma podstaw do odrzucenia hipotezy H₀. OznaJ cza to, że w próbie przypadkowo tylko otrzymano wariancję pomiaróH większą niż hipotetyczna. W gruncie rzeczy nie można powiedzieć, że rozM proszenie wyników pomiarów napięcia tym woltomierzem jest większe niżl założone.

Uwaga. Gdyby w powyższym przykładzie t!ę samą wariancję s ²=0,91 uzyskano z próby dużej, liczącej np. 61 pomiarów, wówczas otrzymali® byśmy wartość statystyki

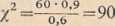
przy 60 stopniach swobody. Ponieważ w tablicy rozkładu #² liczba stopiii swobody k wynosi co najwyżej 30, więc w tym przypadki} należałoby skol szystać z granicznego rozkładu normalnego, do którego dąży rozkład*

Otrzymaną wartość#² przekształcamy na «=V2%²—Jlk— 1 i porówńu-

jemy z wartością u_a zmiennej normalnej N(0,1) odczytaną tak, by P{£/> j^w_a}=0,05. Otrzymalibyśmy wtedy

_w=V2?-V2k-l==V2-90-\/2-60-l=VT8Ó"-VIl9= =13,4- 10,9 «2,5.

Natomiast wartość krytyczna w_a=l,64. Ponieważ znaleźliśmy się tymfl razem w obszarze krytycznym, gdyż w=2,5> l,64=«_a, hipotezę H₀ należałoby odrzucić, co oznaczałoby większą wariancję pomiarów niż założono.] W dużej próbie uzyskana wartość s²=0,9okazała się więc istotnie większa] od założonej wariancji 0,6.

Zadani

\j 2.61. L^iwonano 11 niezależnych pomiarów średnicy odlewanych rur * i otrzymano następujące wyniki (w mm): 50,2, 50,4, 50,6, 50,5, 49,9, 50,0,4 50,3, 50,1, 50,0, 49,6, 50,6. Na poziomie istotności a=0,05 zweryfikować hipotezę, że wariancja uzyskiwanych średnic rur jest 0,04.

<0

j 2.62. Losowa próba w = 200 studentów pewnej uczelni dała wariancję 50 (papierosów)² wypalanych dziennie przez studentów tej uczelni. Ni poziomie istotności a=0,05 zweryfikować hipotezę, że odchylenie M. m dard o we liczby papierosów wypalanych dziennie przez studentów wynosi 5.

2.63. Zużycie po jednym miesiącu pracy pewnej części trącej maszyny, ■/mierzone na 20 wylosowanych częściach, było następujące (ubytek materiału w p): 59,0, 66,7, 69,7, 57,k, 74,9, 67,7£78,9, 67,5.|69,6, 78,3, 80,0, 70,8, 111,0, 78,|:; 73,7, 80,5y'77,5, 69,8, 73,3, 81,5. Na poziomie istotności

- 0,05 zweryfikować hipotezę, że wariancja zużycia tych części maszyny wynosi 40 j.t²

2.64. Na podstawie danych liczbowych z zadania 2.3 zweryfikować nu poziomie istotności a=0,05 hipotezę, że wariancja dochodów studentów badanej uczelni wynosi 30000 (zł)².

2.65. Na podstawie dapych liczbowych z zadania 1.18 zweryfikować na poziomie istotności a^0,01 hipotezę, że odchylenie standardowe zużytego tlenu podćżaś. utleniania tkankowego, wątroby królików badanych w tym doświadczeniu wynosi 12 pi.

2.66. Na podstawie danych liczbowych z zadania 1.46 zweryfikować na poziomie istotności a=0,05 hipotezę, że wariaribja odległości łądowania ml wyznaczonego punktu w badanej populacji skoczków spadochronowych wynosi 15 m².

2.67. Na podstawie danych liczbowych z zadania 1.40 zweryfikować hipotezę, że odchylenie standardowe wyników zawodnika w trójskoku wynosi 30 cm. Przyjąć poziom istotności a = 0,05.

2.68. Na podstawie danych liczbowych z zadania 2.17 zweryfikować hipotezę, że wariancja plonów owsa w indywidualnych gospodarstwach i rolnych pewnej wsi wynosi 0,25 (q/ha)². Przyjąć poziom istotności a = 0,05.

2.69. Na podstawie danych liczbówych z zadania 2.2Ó zweryfikować na poziomie istotności a = 0,10 hipotezę,, że wariancja strat z osypania

lilię ziarna żyta w PGR-ach wynosi 0,05 (%)²

2.70. Na podstawie danych liczbowych z zadania 2.39 zweryfikować na poziomie istotności a=0,05 hipotezę, że wariancja czasu snu pacjentów

[chorych jia chorobę B wynosi 6400 (minut)²