DSC00082 (6)

VI. Równanie różniczkowe zupełne.

I Równanie postaci:

P(x,y)dx+Q(x,y)dy=0

- - • -ł "V

nazywamy równaniem zupełnym, jeżeli P.QeC¹(D) i lewa strona jest różniczką zupełną pewnej funkcji U(x,y), czyli gdy zachodzi warunek:

_n cP dQ

^v<^x-^y,eD: aT ar

Wtedy równanie można zapisać w postaci: dU=0, a więc rozwiązanie ogólne ma postać:

U(x,y) = C.

Przykład 2.

tSrh*feĄF»}*‘"'

I

Rpzwiąać równanie

B ±

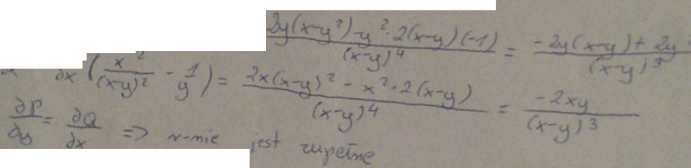
- x . M (»-yf

* ISS )- -

^ ~

u a)

& -o

%-f

j, ) r i ₇*    *    'icĆ7F‘^U-''ⁱ

IL/^y, -iii • ^r '

,    ‘ SAB^f L/j/ = *«liiH .«

\m & ^x ffl

' T, .. '    4#-/

<?

o

71

mato ««--i....—. ■ (anNawocki