DSCF2562

222 6. Zmienne losowe jednowymiarowe

Równość powyższą przekształcamy następująco:

F{x+Ax)-F(:x) F_l{y+Ay)-F_l(y) Ay Ax    Ay    Ax

Z założenia ciągłości funkcji g(x) wynika, że gdy Ax->0, to'Ay-+0, a zatem

F(x+Ax)-F(x) f_t(y+Ay)-F_I(y) J Ay

lun — ■ — -—•== lun ——-- ■    • lim — ,

4x-*o    Ax    Ay-+a . Ay    ax-*oAx

z której otrzymujemy

F'(x)=F\(y)j- lub /(x) =/,(>>)—• dx    dx

Z ostatniej równości mamy

dy

Korzystając z tego, że x=h{y), otrzymujemy

My)=f(h(y))-h'(y).

W przypadku gdy funkcja g(x) jest malejąca, to po analogicznym rozumowaniu otrzymujemy wzórO

Ostatecznie wzór na gęstość f\{y) zmiennej losowej Y zarówno w przypadku, gdy g(x) jest funkcją rosnącą jak i w przypadku, gdy jest funkcją malejącą, jest następujący:

^> (6A1)    fl My) =/ (^h (y)) • I h'(y) I • jl

Przykład 6.4.3. Znając gęstość prawdopodobieństwa f(x) zmiennej losowej X wyznaczyć gęstość prawdopodobieństwa zmiennej losowej Y, jeśli Y=aX+b, przy założeniu, żea^O.

Rozwiązanie. W rozważanym przypadku zależność między wartościami x zmiennej losowej X i wartościami y zmiennej losowej Y dana jest za pomocą funkcji liniowej y-

=ax+fc, tzn. g(x)=ax+6. Funkcją odwrotną h(y) jest x=—y — —. Korzystając ze

, a a

wzoru (6.4.1) otrzymujemy:

(6.4.2)

(') Jeżeli funkcja g{x) jest malejąca i ma pochodną g*(a), to spełnia ona warunek #(x)<0. Funkcj* odwrotna ma te same własności.

Przykład 6.4.4. Zmienna losowa X podlega rozkładowi /(x)=-7=^exP (—|x²),

V2tc

— co <x< co (tzw. rozkład normalny, § 6.10). Wyznaczyć rozkład /iOO zmiennej losowej Y=2X-3.

Rozwiązanie. Bezpośrednio ze wzoru (6.4.2) mamy

® 'P $

ZiOO = —t= exp (-1 (y+3)²).

2\j2n

Przykład 6.4.5. Zmienna losowa X podlega rozkładowi

.    (0    dla    x<0,

f(x)=<

(2exp(—2x) dla x>0.

Wyznaczyć rozkład f_x(y) zmiennej losowej Y=X².

Rozwiązanie. W rozważanym przykładzie funkcja y=x² posiada funkcję odwrotną x=_sfy w obszarze danych wartości zmiennej losowej X, a zatem h(y)=y/y. Korzystając ze wzoru (6.4.1) otrzymujemy:

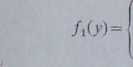
—i©"    dla    0,

1 ' ' _

z~rfUy) ^d,a y^>0‘

_ 2 V.v

Uwzględniając daną postać funkcji f(x), mamy

JO    dla

¹ ^    lj^,-łexp(-2_>/J’) dla y> 0,

czyli gęstość postaci rozkładu Weibulla (6.3.11).

Przykład 6.4.6. Zmienna losowa X podlega rozkładowi

MBi i.    .

/(x)=-p=rexp(—~x),    — oo <y<co.

v2it

Wyznaczyć rozkład zmiennej losowej Y—X².

Rozwiązanie. Ponieważ w rozważanym przykładzie funkcja y^jc¹ nie posiada funkcji odwrotnej w całym obszarze możliwych wartości zmiennej losowej X, nie możemy posługiwać się bezpośrednio wzorem (6.4.1). Postąpimy w tym przypadku następująco:

a)    Wyznaczamy dystrybuantę F_x(y) zmiennej losowej Y

F_l(y)=P<.Y<y)=P(X²<y)~P(-Jy<X<_%fi)~FU]>)-F(-Jy).

b)    Gęstość /i(j>) zmiennej losowej Y wyznaczamy ze związku

fi(y)=F\(y).