Tomasz Kowalski

Wykłady z matematyki dla studentów kierunków ekonomicznych

Wykład 7 i 8

FUNKCJE – Lista zadań

1

. Znaleźć w postaci

funkcję odwrotną do funkcji określonej wzorem:

)

(

1

x

f

y





a) , b)

1

2

)

(







x

x

f

y

1

3

3

)

(









x

x

x

f

y

, c)

2

1

2

)

(









x

x

x

f

y

.

2. Rozwiązać równania lub nierówności:

a)

2

5

1

2

4

x



 , b)

3

4

3

1

3

3

x





, c)

, d)

1



e

x

5

3

e

e

x







, e)

e

e

e

x



2

2

, f)

e

e

x



2

)

1

(

.

3. Podać wartości logarytmów:

a)

2

log

2 , b)

5

3

log

9 , c)

4

1

log

8

, d)

, e)

, f)

2

ln e

1

ln

3

ln e .

4. Rozwiązać równania lub nierówności:

a)

2

1

ln



x

, b)

, c)

2

ln



x

3

1

ln



x

, d)

1

ln





x

.

5. Zbadać parzystość funkcji:

a)

x

x

x

x

e

e

e

e

x

f











)

(

, b)

4

4

ln

)

(







x

x

x

f

.

6. Obliczyć wartości następujących wyrażeń:

a)

, b)

0

arccos

2

1

sin

arc

, c)

)

2

3

sin(

arc



, d)

)

2

1

cos(

arc



, e)

, f)

1

arctg

)

3

(

arctg



.

7. Znaleźć złożenie

funkcji

określonych wzorami:

f

g 

R

R

g

R

R

f





:

i

:

a)

, b)

, c)

.

x

x

x

g

x

x

f

3

)

(

,

2

3

)

(

2









2

2

)

(

,

1

)

(

x

x

g

x

x

f







2

)

(

,

sin

)

(

x

x

g

x

x

f





8. Wyznaczyć funkcje złożone:

, jeżeli

.

g

g

f

f

g

f

f

g









,

,

,

x

x

x

g

x

x

f

7

3

)

(

,

5

2

)

(

2









9. Funkcję h przedstawić w postaci złożenia

:

f

g 

a)

, b)

, c)

, d)

?

2

)

5

4

(

)

(



 x

x

h

x

x

h

3

sin

)

(



5

2

3

)

(





x

x

h

)

4

ln(

)

(

2





x

x

h

10. Sporządzić wykres funkcji

, a następnie wykresy pozostałych funkcji stosując odpowiednie

przekształcenia:

.

)

(x

f

y



x

3

,

log



x

y

x

y

x

y

x

f

y

3

3

3

log

,

1

log

),

2

(

log

)

(















11. Wyznaczyć w postaci

funkcję odwrotną do

)

(

1

x

f

y





)

(x

f

y



. Naszkicować wykresy obu funkcji.

a)

, b)

, c)

2

3

)

(





x

x

f

2

2

)

(





x

x

f

)

2

ln(

)

(





x

x

f

, d)

.

1

)

(





x

e

x

f

Funkcje - lista zadań

2

Odpowiedzi

1. a)

1

1

( )

2

2

y

f

x

x









1

, b)

1

3

( )

3

x

y

f

x

x









 

, c)

1

2

1

( )

2

x

y

f

x

x











.

2. a)

7
2

x

  , b)

11

9

x



, c)

, d)

0

x



1
2

x

 , e)

1
4

x

  , f )

1
2

x

 .

3. a)

1
2

, b)

2
5

, c)

3
2

 ,

d)

2, e)

0, f)

3
2

.

4. a) x

e



, b)

2

0 x e

  , c)

3

x

e



,

d)

1

0 x

e

  .

5. a)

jest zbiorem symetrycznym względem zera,

\ {0}

D

R



(

)

( )

f

x

f x

  

- funkcja jest nieparzysta,

b)

jest zb. symetr. względem zera, ,

(

; 4) (4;

)

D

   



(

)

( )

f

x

f x

  

- funkcja jest nieparzysta.

6. a)

2



, b)

6



, c)

3



 , d)

2
3



,

e)

4



, f)

3



 .

7. a)

, b)

2

2

(

)( ) (3

2)

3(3

2) 9

21

10

g

f

x

x

x

x

x

















2

2

4

2

(

)( ) (

1)

2

g

f

x

x

x

x

1













,

c)

2

(

)( ) sin

g

f

x

x





.

8.

,

2

2

(

)( ) 3(2

5)

7(2

5) 12

74

110

g

f

x

x

x

x

x







 







2

2

(

)( ) 2(3

7 ) 5 6

14

f

g x

x

x

x

x

5





 







,

, (

(

)( ) 2(2

5) 5 4

15

f

f

x

x

x



  





2

2

2

4

3

2

)( ) 3(3

7 )

7(3

7 ) 27

126

168

49

g g x

x

x

x

x

x

x

x



















x



.

9. a)

albo

2

( )

,

( ) 4

5

g x

x

f x

x





2

( ) (

5) ,

( ) 4

g x

x

f x





 x , b)

3

( )

,

( ) sin

g x

x

f x

x





,

c)

albo

( ) 3 ,

( ) 2

5

x

g x

f x

x







5

( ) 3

,

( ) 2

x

g x

f x



x





,

d)

albo

2

( ) ln ,

( )

4

g x

x

f x

x







2

( ) ln(

4),

( )

g x

x

f x

x







.

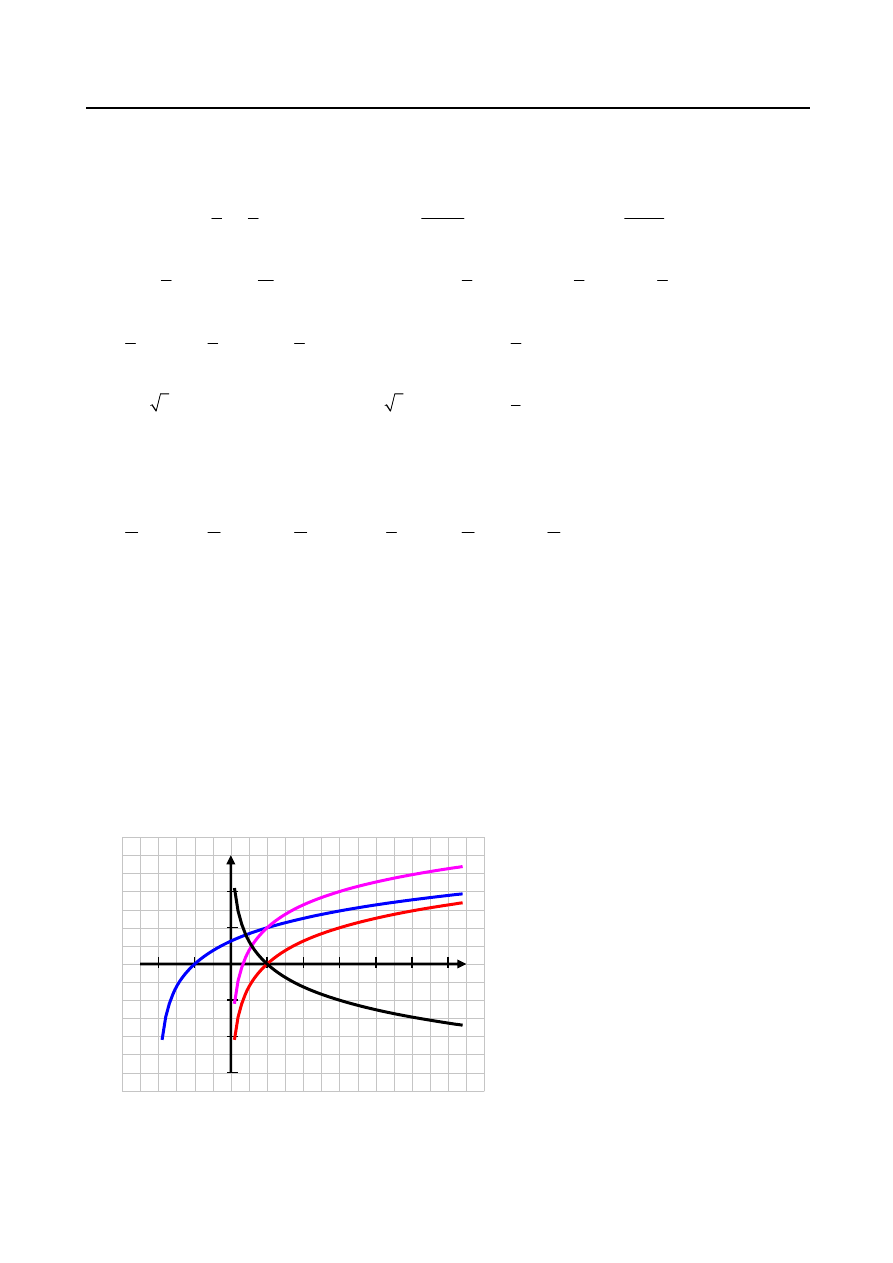
10.

-2 1

2

4

5

6

-2

1

2

x

y

O

3

log

1

y

x





3

log

y

x



3

log (

2)

y

x





3

log

y

x

 

Funkcje - lista zadań

3

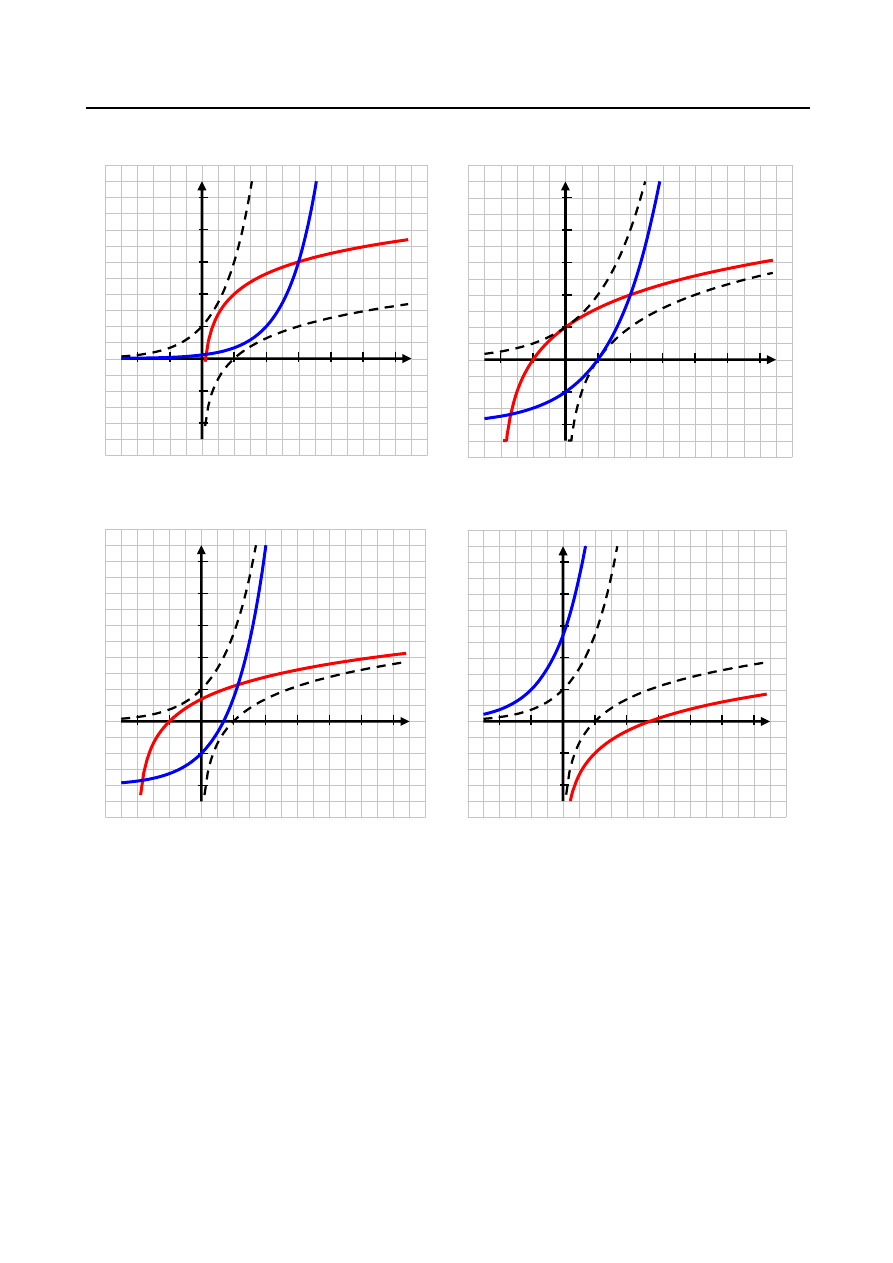
11. a)

,

b)

1

3

( ) log

2

y

f

x

x









1

2

( ) log (

2)

y

f

x

x









,

c)

,

d)

1

( )

2

x

y

f

x

e









1

( ) ln

1

y

f

x

x







 .

-2

-1

1

2

3

4

5

6

-2

-1

1

2

3

4

5

x

y

O

5

y

3

x

y



2

3

x

y





3

log

y

x



3

log

2

y

x





-2

-1

1

2

3

4

5

6

-2

-1

1

2

3

4

x

O

2

2

x

y





2

x

y



2

log

y

x



2

log (

2)

y

x





-2

-1

1

2

3

4

5

6

-2

-1

1

2

3

4

5

x

y

O

x

y

e



2

x

y

e





ln

y

x



ln(

2)

y

x





-2

-1

1

2

3

4

5

6

-2

-1

1

2

3

4

5

x

y

O

x

y

e



ln

y

x



1

x

y

e





ln

1

y

x



