Tomasz Kowalski

Wykłady z matematyki dla studentów kierunków ekonomicznych

Wykład 13

ZASTOSOWANIA RACHUNKU RÓŻNICZKOWEGO

FUNKCJI JEDNEJ ZMIENNEJ

1. Badanie funkcji

Badanie funkcji ma na celu uzyskanie wyczerpujących informacji o tej funkcji potrzebnych do sporzą-
dzenia wykresu. Schemat badania funkcji:
1. Analiza funkcji:
-

określenie dziedziny,

- obliczenie granic na końcach przedziałów określoności,
- znalezienie równań ewentualnych asymptot,
- wyznaczenie punktów przecięcia wykresu z osiami układu współrzędnych,
- zbadanie, czy funkcja ma istotne dla jej zmienności własności szczególne, np. parzystość, nieparzystość,
okresowość).
2. Obliczenie i analiza pochodnej funkcji:
- wyznaczenie przedziałów monotoniczności funkcji,
- znalezienie ekstremów i określenie ich rodzaju.
3. Obliczenie i analiza drugiej pochodnej funkcji:
- wyznaczenie przedziałów wklęsłości i wypukłości wykresu,
- znalezienie punktów przegięcia wykresu.
4. Sporządzenie tabelki zmienności na podstawie wyników z części 1-3.
5. Naszkicowanie wykresu.

Przykład 1. Zbadać funkcję i sporządzić jej wykres: a)

, b)

x

x

x

x

f

4

4

)

(

2

3







3

3

3

)

(

2

2







x

x

x

f

,

c)

2

5

4

)

(

2









x

x

x

x

f

, d)

1

)

(





x

x

e

x

f

, e)

x

x

x

f

ln

)

(



.

Rozwiązanie.

a) Dziedziną funkcji jest

R

D

 . Funkcja nie posiada zatem asymptot pionowych.

Ponieważ























)

4

4

1

(

lim

)

4

4

(

lim

2

3

2

3

x

x

x

x

x

x

x

x

oraz























)

4

4

1

(

lim

)

4

4

(

lim

2

3

2

3

x

x

x

x

x

x

x

x

,

to funkcja nie posiada asymptot poziomych , może jednak posiadać asymptoty ukośne.

Jednakże





















)

4

4

(

lim

)

(

lim

2

x

x

x

x

f

m

x

x

i podobnie





















)

4

4

(

lim

)

(

lim

2

x

x

x

x

f

m

x

x

.

Oznacza to ostatecznie, że asymptot ukośnych nie ma.

Obliczając wartość funkcji w punkcie

otrzymujemy

0



x

0

)

0

(



f

, co oznacza, że wykres przechodzi przez

początek układu współrzędnych . Poszukując odciętych punktów wspólnych wykresu z osią OX
dostajemy

)

0

,

0

(

P

2

,

0

0

)

4

4

(

0

4

4

0

)

(

2

1

2

2

3

























x

x

x

x

x

x

x

x

x

f

.

Tym samym dodatkowym punktem wykresu leżącym na osi OX jest

.

)

0

,

2

(

Q

Pochodna funkcji jest równa

. Szkic jej wykresu przedstawia rys.1.

4

8

3

)

(

2

/







x

x

x

f

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

2

-

-

-

+ +

Znak

/

f

X

+ +

3

2

2

Rys. 1.

Obliczając drugą pochodną otrzymujemy

. Szkic wykresu przedstawia rys.2.

8

6

)

(

//



 x

x

f

Znak

//

f

X

3

4

+ + +

_ _ _

Rys. 2.

Układamy tabelkę zmienności:

x

)

0

;

(



0

)

;

0

(

3

2

3

2

)

;

(

3

4

3

2

3

4

)

2

;

(

3

4

2

)

;

2

(





/

f

+ + 0

–

–

0 +

//

f

–

– – + +

f





0

27

32

max.

27

16

p.p

min.

0





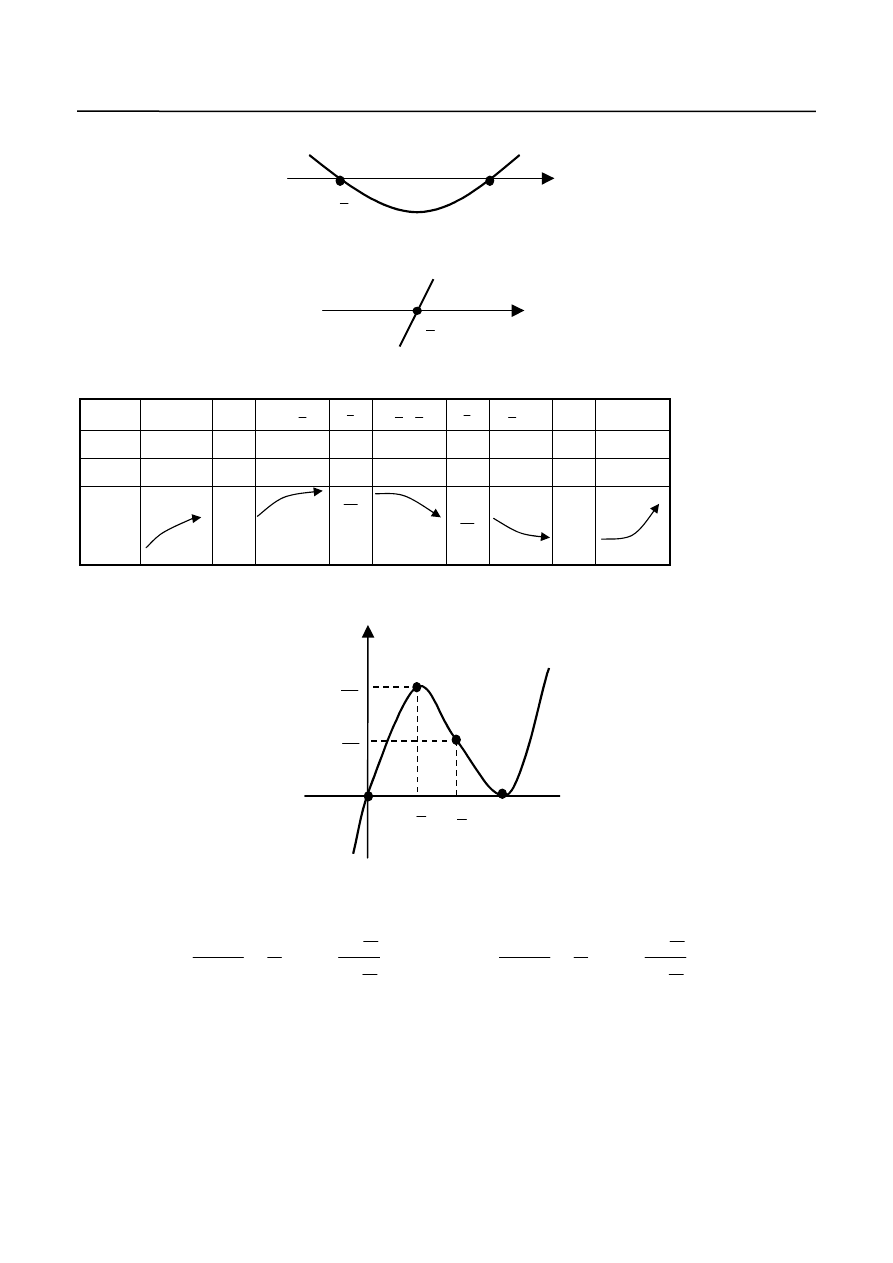
Wykres funkcji przedstawiony jest na rys.3.

X

3

2

Y

0

3

4

27

16

27

32

2

x

x

x

x

f

4

4

)

(

2

3







Rys. 3.

b) Dziedziną funkcji jest

R

D

 . Funkcja nie posiada zatem asymptot pionowych.

Ponieważ

3

1

3

lim

3

3

3

lim

2

3

2

3

2

2

]

[



























x

x

x

x

x

x

oraz

3

1

3

lim

3

3

3

lim

2

3

2

3

2

2

]

[



























x

x

x

x

x

x

,

to prosta

jest asymptotą poziomą obustronną funkcji i tym samym asymptot ukośnych wykres nie

posiada.

3



y

Obliczając wartość funkcji w punkcie

otrzymujemy

0



x

1

)

0

(





f

, co oznacza, że wykres przecina oś OY

w punkcie

. Poszukując odciętych punktów wspólnych wykresu z osią OX dostajemy

)

1

,

0

(



P

1. Tym samym punktami wykresu leżącymi na osi OX są

,

.

,

1

0

3

3

0

)

(

2

1

2

















x

x

x

x

f

)

0

,

1

(

1



Q

)

0

,

1

(

2

Q

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

3

Ponieważ

)

(

3

3

3

3

)

(

3

)

(

3

)

(

2

2

2

2

x

f

x

x

x

x

x

f





















, dla każdego

R

x

 , to funkcja jest parzysta.

Pochodna funkcji jest równa



























2

2

2

2

2

2

/

2

2

2

/

2

/

)

3

(

2

)

3

3

(

)

3

(

6

)

3

(

)

3

)(

3

3

(

)

3

(

)

3

3

(

)

(

x

x

x

x

x

x

x

x

x

x

x

f

2

2

)

3

(

24



x

x

.

Ponieważ w rozpatrywanej dziedzinie mianownik wyrażenia jest dodatni, to znak pochodnej jest identyczny
jak znak funkcji

, której szkic wykresu przedstawiony jest na rys.4.

x

x

g

24

)

(



Znak

/

f

0

  

  

Rys. 4.

Obliczając drugą pochodną otrzymujemy:



























4

2

2

2

2

4

2

/

2

2

2

2

/

//

)

3

(

2

)

3

(

2

24

)

3

(

24

)

3

(

]

)

3

[(

24

)

3

(

)

24

(

)

(

x

x

x

x

x

x

x

x

x

x

x

f

3

2

2

4

2

2

2

2

)

3

(

)

3

3

(

24

)

3

(

)

4

3

)(

3

(

24

















x

x

x

x

x

x

.

W rozpatrywanej dziedzinie znak drugiej pochodnej jest identyczny jak znak funkcji

, której

szkic wykresu przedstawiony jest na rys.5.

2

3

3

)

(

x

x

h





+ + +

- -

Znak

//

f

X

- -

1



1

Rys. 5.

Układamy tabelkę zmienności:

x

)

1

;

(





-1

)

0

;

1

(



0

)

1

;

0

(

1

)

;

1

(





/

f

-

-

0 + +

//

f

-

0 + + 0

-

f

1

0

p.p.

min.

-

1

0

p.p.

1

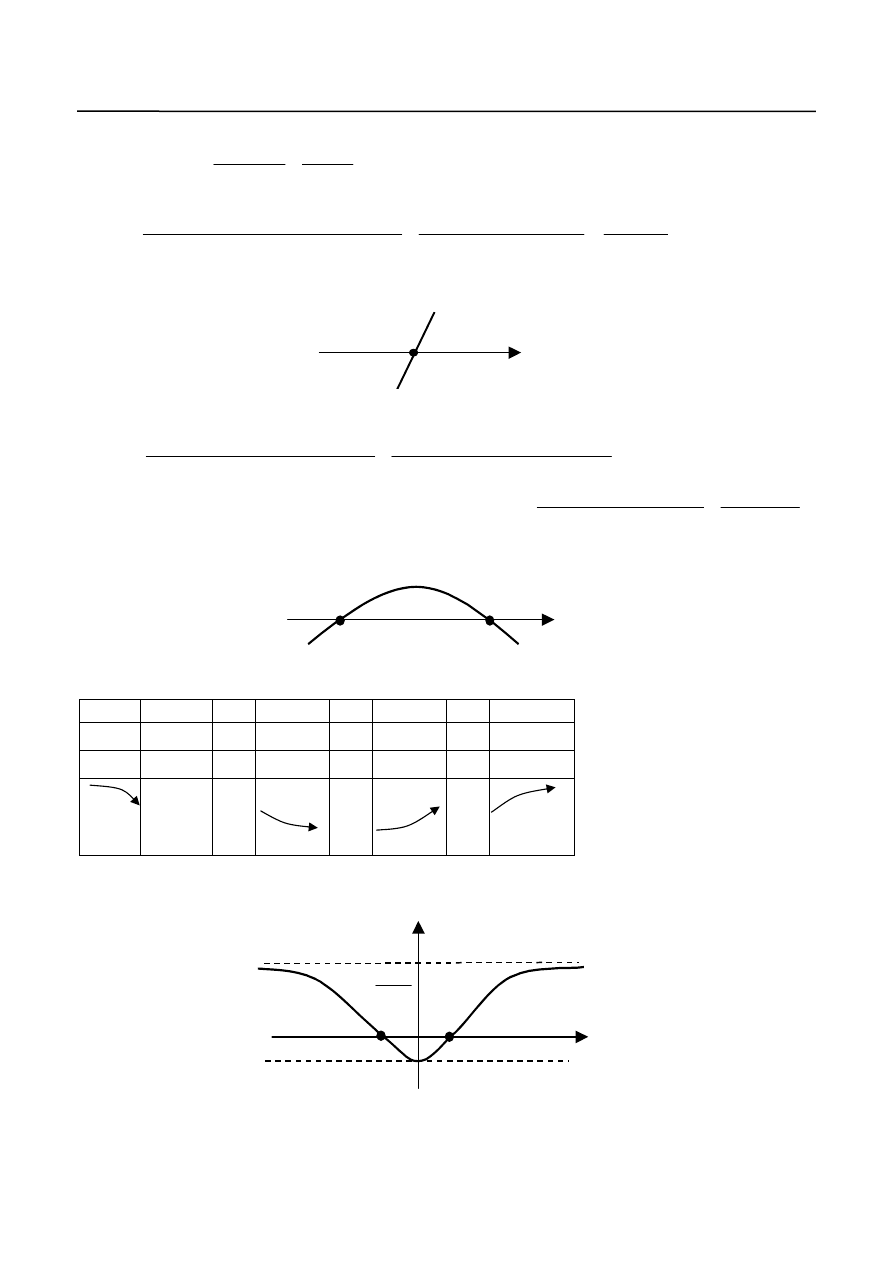
Wykres funkcji przedstawiony jest na rys.6.

3

3

3

)

(

2

2







x

x

x

f

X

1



-1

Y

1

3

Rys. 6.

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

4

c) Funkcja

2

5

4

)

(

2









x

x

x

x

f

0

2





x

, zatem

)

;

2

(

)

2

;

(









D

.

jest okre

na, gdy

ślo



Ponieważ











]

[

1

5

4

2

x

x

,









0

2

lim

2

x

x











]

[

1

5

4

lim

2

x

x

,











0

2

2

x

x

to prosta

jest asymptotą pionową obustronną wy resu funkcji. Z faktu, że

2



x

k







































]

[

]

[

1

1

4

lim

2

5

4

lim

2

5

2

x

x

x

x

x

x

x

x

,

























]

[

]

[

4

lim

5

4

lim

2

x

x

x

x

,









1

1

2

2

5

x

x







x

x

wynika, że wykres nie posiada asymptot poziomych, może jednak posiadać asymptoty ukośne.
Ponieważ

1

1

1

lim

2

5

4

lim

)

(

lim

2

2

5

4

2

2

]

[







































x

x

x

x

x

x

x

x

x

x

x

x

f

m

,









































2

2

5

4

lim

)

2

5

4

(

lim

]

)

(

[

lim

2

2

2

x

x

x

x

x

x

x

x

x

mx

x

f

n

x

x

x

2

1

2

5

2

lim

[











x

lim

2

2

5

]

























x

x

x

x

.

x

oraz granice przy





x

s

ą ukośną obustronną jest prosta

2



 x

y

.

0 wynosi

ą analogiczne, to asymptot

Wartość funkcji w punkcie



x

2

5

)

0

(





f

, że wykres przecina oś OY w punkcie

. Oznacza to

)

2

,

0

(



P

. Równanie

0

)

(

5



x

f

przyjmuje postać

i jest równaniem sprzecznym (

0

5

4

2





 x

x

0





).

Wykres nie przecina osi OX.
Obliczając pochodną otrzymujemy:





















2

/

2

/

2

/

)

2

(

)

2

)(

5

4

(

)

2

(

)

5

4

(

)

(

x

x

x

x

x

x

x

x

f















2

2

)

2

(

)

5

4

(

)

2

)(

4

2

(

x

x

x

x

x

2

2

2

3

4

)

5

4

8

4

















x

x

x

x

x

x

2

2

)

2

(

)

2

(

4

2









x

x

x

.

Znak pochodnej jest identyczny jak znak trójmianu

, którego szkic wykresu przedstawio-

ny jest na rys.7.

3

4

)

(

2







x

x

x

g

+ +

-

Znak

/

f

-

X

- -

+ +

1

2

3

Rys. 7.

Obliczając drugą pochodną otrzymujemy:





















4

/

2

2

2

/

2

//

)

2

(

]

)

2

)[(

3

4

(

)

2

(

)

3

4

(

)

(

x

x

x

x

x

x

x

x

f

















4

2

2

)

2

(

)

2

(

2

)

3

4

(

)

2

)(

4

2

(

x

x

x

x

x

x

4

)

2

(





x

2

)]

3

4

(

2

)

2

)(

4

2

)[(

2

(













x

x

x

x

x

4

4

)

2

(

)

2

(









x

x

2

2

)

2

(

2

)

6

8

2

8

8

2

)(

2

(















x

x

x

x

x

x

.

W rozpatrywanej dziedzinie znak drugiej pochodnej jest identyczny jak znak funkcji

, której

szkic wykresu przedstawiony jest na rys.8.

2

)

(



 x

x

h

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

5

  

Znak

//

f

2

  

Rys. 8

Układamy tabelkę zmienności:

0

.

x

)

0

;



(

)

0

(

1

;

1

)

1

(

2

;

2

)

2

(

3

;

3

)

;

3

(





/

f

+ +

–

+

0

–

X

0

//

f

–

–

–

+ +

X

f

min.

2









2



max.

5

- 2

X
X
X
X

 





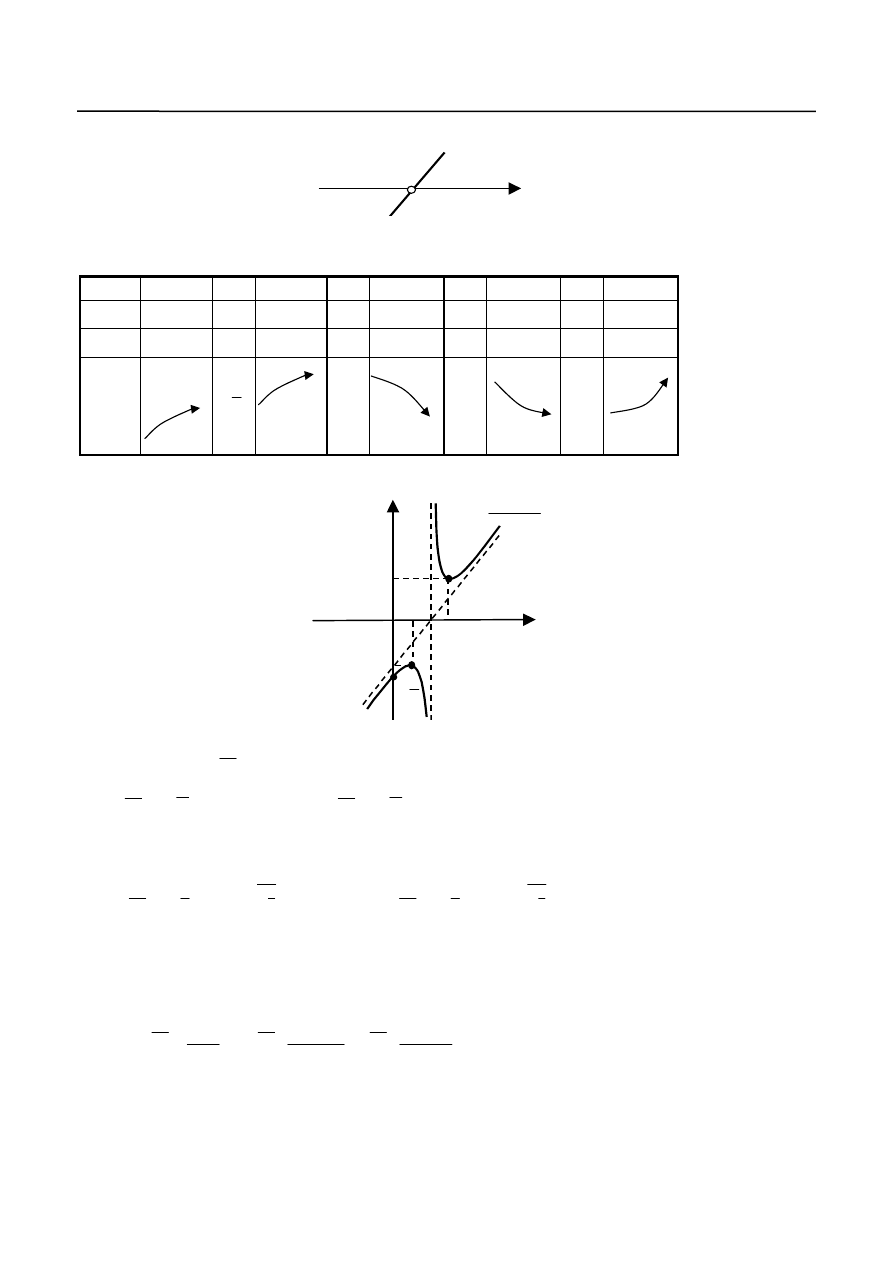
Wykres funkcji przedstawiony jest na rys.9.

2

Y

X

2

5

4

)

(

2









x

x

x

x

f

y

x

  2

2 3

1

-2

2

5



Rys. 9.

1

)

(





x

x

e

x

f

jest określona, gdy

0

1





x

, zatem

;

(





D

)

;

1

(

)

1







.

d) Funkcja

0

lim

]

[

]

[

0

1

1

1



















e

e

e

x

x















x

,





1

x

ową praw



]

[

]

[

0

1

1

lim

e

e

e

x

x

.

Prosta 1 jest asymptotą pion

ostronną wykresu funkcji.



x

Z faktu, że

e

e

x















1

1

1

1

]

[

oraz

e

e

e

e

x

x















1

1

1

1

lim

lim

]

[

,

x

x

x









ę poziomą obustronną o równaniu

e

e

x

x

lim

lim

x

x









e

y



wynika, że wykres posiada asymptot

.

Wartość funkcji w punkcie

wynosi

0



x

1

)

0

(



f

sprzeczny

. Oznacza to, że wykres przecina oś OY w punkcie

. Równanie

jest równaniem

m. Wykres nie przecina osi OX (leży powyżej osi).

)

1

,

0

(

P

0

)

(



x

f

Obliczając pochodną otrzymujemy:

2

1

2

1

/

1

/

1

)

(

)

(



















e

x

x

e

x

e

x

f

x

x

)

1

(

1

)

1

(

1













x

x

x

x

x

x

x

.

W rozpatrywanej dziedzinie pochodna jest ujemna.

Obliczając drugą pochodną otrzymujemy:

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

6















4

2

)

1

(

)

1

(

x

x

































/

2

1

2

/

1

/

1

//

]

)

1

[(

)

1

(

)

(

)

(

x

e

x

e

e

x

f

x

x

x

x

x

x





4

)

1

(x



















1

2

2

1

)

1

(

2

)

1

(

)

1

(

1

x

e

x

x

e

x

x

x

x

4

1

4

1

4

1

1

)

1

(

)

1

2

(

)

1

(

)

2

2

1

(

)

1

(

)

1

(

2





































x

x

e

x

x

e

x

x

e

e

x

x

x

x

x

x

x

x

.

W rozpatrywanej dziedzinie znak drugiej pochodnej jest identyczny jak znak funkcji

, której

szkic wykresu przedstawiony jest na rys.10.

1

2

)

(



 x

x

h

  

Znak

//

f







1

2

X

Rys. 10.

Układamy tabelkę zm nności

0

ie

:

x

)

0

;

(



)

;

1

0

(

2

2

1

)

1

;

(

2

1

1

)

;

1

(





/

f

–

–

–

–

X

//

f

–

– 0 +

+

X

f

e

1

e

1

p.p.

0

X
X
X
X

 

e

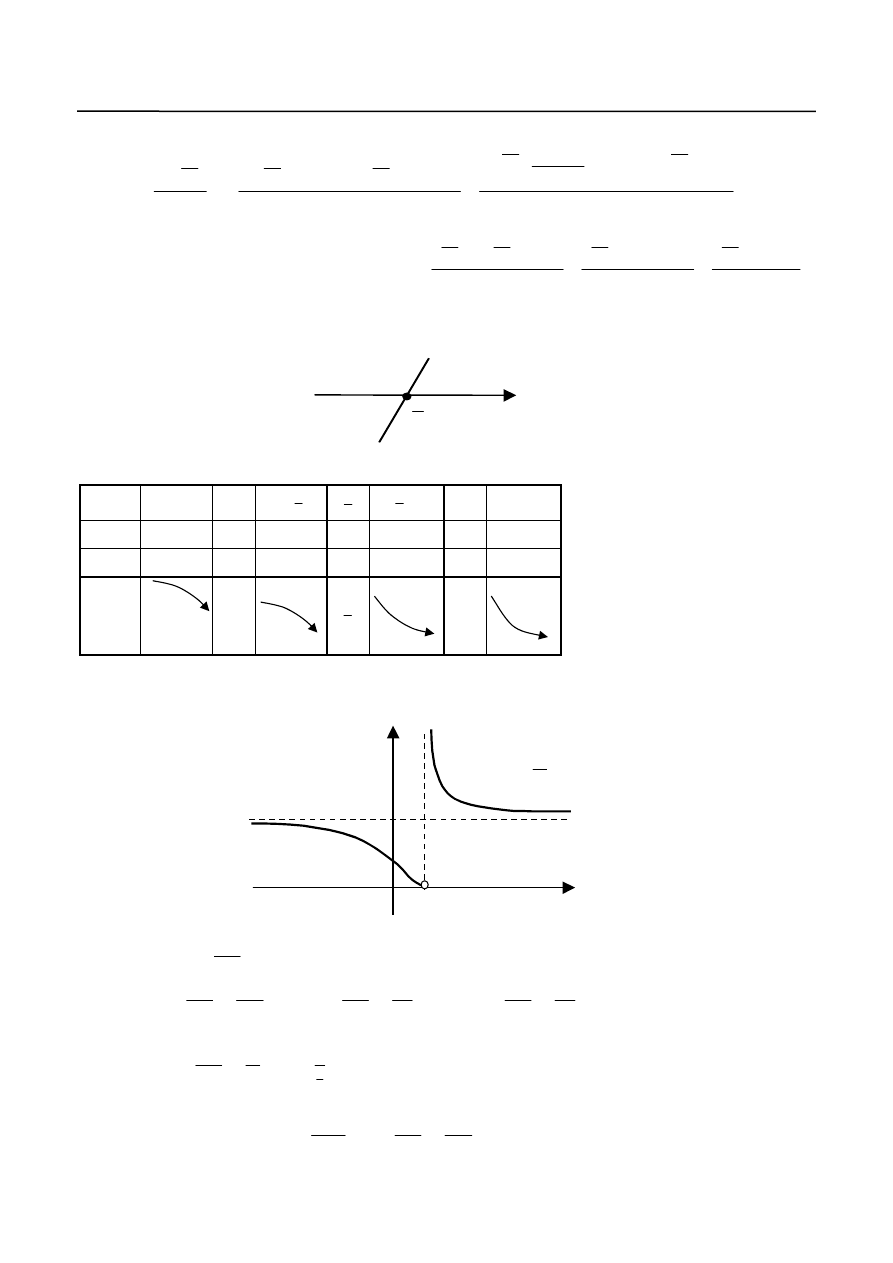
Wykres funkcji przedstawiony jest na rys.11.

1

)

(





x

x

e

x

f

1

1

e

Y

X

Ry

e) Funkcja

s. 11.

x

x

x

f

ln

)

(



jest określona, gdy

i

0



x

0

ln



x

. Zatem

)

;

1

(

)

1

;

0

(









D

.

Ponieważ

0

ln

lim

0













x

x

,

0

]

[

x











ln

lim

1

x

x



]

[

0

1

x

,













]

[

0

1

ln

lim

1

x

x

x

, to asymptotą pionową jest

1



x

.

Z faktu, że

















x

x

ln

lim











x

x

x

x

H

lim

1

lim

1

]

[

wynika, że funkcja nie posiada asymptoty poziomej,

x

może natomiast posiadać asymptotę ukośną.

W tym wypadku jednak

0

1

ln

]















x

x

m

x

x

, co oznaczałoby, że asymptota jest poziom

a taka nie istnieje.

1

lim

)

(

lim

[







x

f

a,

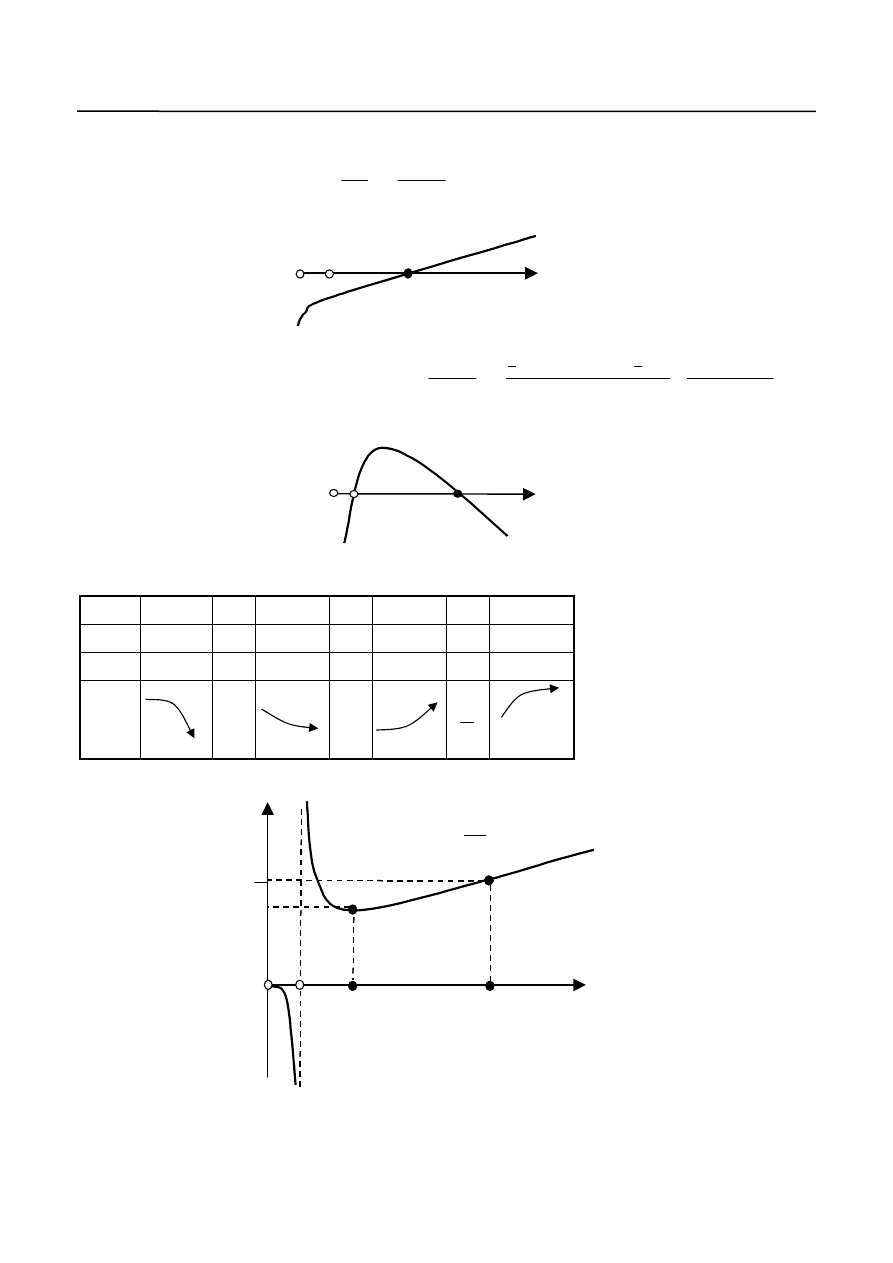
Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

7

Wykres funkcji nie przecina osi układu współrzędnych.

Pochodna funkcji jest równa

x

x

x

x

x

f

2

/

/

ln

1

ln

)

ln

(

)

(







czny jak znak funkcji

. Mianownik wyrażenia jest w zbiorze D dodatni,

zatem znak pochodnej jest identy

1

ln

)

(



 x

x

g

. Szkic jej wykresu przedstawia rys.12.

0 1

+ +

Znak

/

f

X

e

_ _ _

Rys. 12.

Obliczając drugą pochodną otrzymujemy

x

x

x

x

x

x

x

x

x

x

x

f

x

x

4

4

2

2

1

/

2

//

ln

)

ln

2

(

ln

ln

ln

)

1

(ln

ln

)

ln

1

ln

(

)

(

















.

jak znak funkcji

)

ln

2

(

ln

)

(

x

x

x

h

Znak pochodnej jest w zbiorze D taki sam





. Szkic wykresu tej funkcji

przedstawia rys.13.

+ + +

Znak

//

f

0

-

X

2

e

_ _

1

Rys. 13.

Układamy tabelkę zm

ności

ien

:

x

)

1

;

0

(

1

)

1

(

e

;

e

)

;

(

2

e

e

2

e

)

;

(

2



e



/

f

–

–

+

+

X

0

//

f

–

X +

+

–

0

f

0

X
X





e

min.

2

2

e

p.p





X





Wykres funkcji przedstawiony jest na rys.14.

2

2

e

0

2

e

1

x

x

x

f

ln

)

(



X

Y

e

e

Rys. 14.

Wykład 13. Zastosowania rachunku różniczkowego funkcji jednej zmiennej

8

2. Najmniejsza i największa wartość funkcji na przedziale

Niech f będzie funkcją ciągłą na przedziale domkniętym

b

a ;

. Z twierdzenia Weierstrassa wynika,

że istnieją punkty

b

a

x

x

;

,

2

1



, takie że

m

x

f



)

(

1

,

M

x

f



)

(

2

, gdzie m oznacza wartość najmniejszą

funkcji na przedziale, a M - wartość największą.
Jeżeli dodatkowo założyć, że funkcja f jest różniczkowalna w przedziale, to punktami, w których mogą
wystąpić te wartości są : a) końce przedziału, b) punkty wewnętrzne, w których występuje ekstremum.

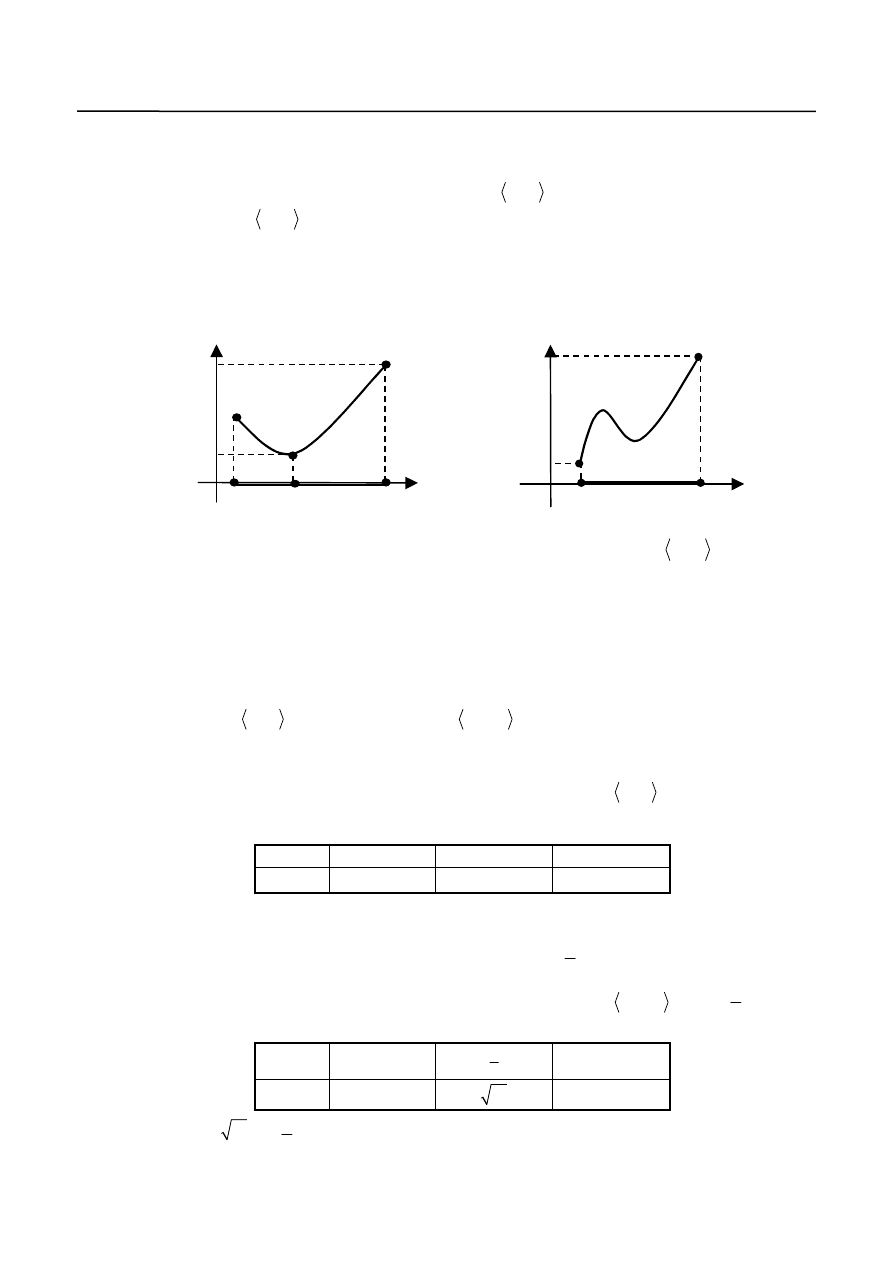
Przypadki te zilustrowane zostały na rys.15.

Y

X

a

x

1

b

x



2

M

m

y

f x

 ( )

Y

X

b

x



2

a

x



1

M

m

y

f x

 ( )

Rys. 15.

Uwaga.

Aby znaleźć wartość najmniejszą i największą funkcji f na przedziale

a b

;

w przypadku,

gdy funkcja jest różniczkowalna wystarczy:
1. Wyznaczyć punkty, w których pochodna jest równa zeru (punkty takie nazywamy stacjonarnymi) leżące

w przedziale.

2. Obliczyć wartości funkcji na końcach przedziału oraz w punktach stacjonarnych wyznaczonych w 1.
Największa z obliczonych wartości funkcji jest wtedy wartością największą, najmniejsza-najmniejszą.

Przykład 2.

Wyznaczyć wartość najmniejszą i największą funkcji

)

(x

f

y



na przedziale I :

a)

,

3

3

)

(

x

x

x

f





2

;

0



I

, b)

3

;

2

,

)

(

2









I

e

x

f

x

x

.

Rozwiązanie.
a) Ponieważ

, to

.

2

/

3

3

)

(

x

x

f





1

,

1

0

3

3

0

)

(

2

1

2

/

















x

x

x

x

f

Wynika stąd, że jedynym punktem stacjonarnym leżącym wewnątrz przedziału

2

;

0

jest

.

1



x

W poniższej tabelce zestawiono wartości funkcji na końcach przedziału i w punkcie stacjonarnym:

x

0 1 2

f x

( )

0 2 2



Wynika z nich, że )

1

(

2

),

2

(

2

f

M

f

m











.

b) Ponieważ

2

/

( )

(1 2 )

x x

f x

e

x







, to

2

1

0

2

1

0

)

(

/















x

x

x

f

.

Wynika stąd, że jedynym punktem stacjonarnym leżącym wewnątrz przedziału

3

;

2



jest

2

1



x

.

Mamy zatem:

x

2



2

1

3

f x

( )

2

e

4

3

e

12

e

Oznacza to, że

4

3

12

1

( ),

(3)

2

m

e

f

M

e

f









.