Tomasz Kowalski
Wykłady z matematyki dla studentów kierunków ekonomicznych
Wykład 7
FUNKCJE. PODSTAWOWE OKREŚLENIA I WŁASNOŚCI
1. Pojęcie funkcji. Dziedzina. Przeciwdziedzina. Wykres
Niech dane będą zbiory X i Y. Funkcją f nazywać będziemy przyporządkowanie każdemu elementowi
ze zbioru X dokładnie jednego elementu
y
ze zbioru Y . Piszemy wtedy
lub
,
.
Y
X
f
:
)
(x
f
y
X
x
Zbiór
X nazywamy dziedziną funkcji, element
X
x
- argumentem funkcji. Element
przyporządkowany elementowi
oznaczamy
Y
y
X
x
)
(
x
f
y
i nazywamy wartością funkcji w punkcie
x .
Zbiór wszystkich wartości danej funkcji nazywamy przeciwdziedziną
.
Od tej pory zajmować się będziemy wyłącznie funkcjami, które określone są w pewnym podzbiorze
zbioru liczb rzeczywistych
R (przedziale lub sumie przedziałów), a wartości są liczbami rzeczywistymi.
Funkcję określać będziemy najczęściej za pomocą wzoru (wzorów). Jeżeli dziedzina takiej funkcji nie będzie
wyraźnie wskazana, to przyjmować będziemy, że jest nią zbiór wszystkich
x, dla których prawa strona wzoru
ma określoną wartość. Tak rozumianą dziedzinę nazywać będziemy dziedziną naturalną funkcji i oznaczać
symbolem
D lub
. Przeciwdziedzinę oznaczać będziemy przez
f
D
1
D lub
.
1
f
D
Przykład 1.
Dziedziną naturalną funkcji
3
)
(
x
x
f
jest zbiór
)
;
3
}
0
3
:
{
x
R
x
D
f
.
Funkcja przyjmuje każdą wartość nieujemną, zatem
;
0
1
f
D
.
Daną funkcję
f o dziedzinie naturalnej D można rozpatrywać na pewnym podzbiorze
D
A
. Funkcję
nazywamy wtedy zredukowaną do zbioru
A i oznaczamy przez
A
f .
Uwaga. Funkcje występujące w zastosowaniach ekonomicznych są pewnymi funkcjami zredukowanymi
do zbioru wyznaczonego przez istotę rozpatrywanego zjawiska (najczęściej do przedziału
)
;
0
).
Niech
. Wykresem funkcji nazywamy zbiór punktów płaszczyzny
XOY, których współrzędne
x, y spełniają warunek:
(rys.1).
Y
X
f
:
)
(
,
x
f
y
X
x
Uwaga. W praktyce, w celu sporządzenia wykresu funkcji w pewnym przedziale (zawierającym się
w dziedzinie) wybieramy kilka punktów tego przedziału:
i obliczamy wartości funkcji:
. Następnie w układzie kartezjańskim XOY nanosimy punkty:
,
,
,
...,
i łączymy je linią.
n
x
x
x
x
...,
,
,
,
3
2
1
)
(
,
...
),
(
),
(
),
(
3
2
1
n
x
f
x
f
x
f
x
f
))
(
,
(
2
2
x
f
x
))
(
,
(
3
3
x
f
x
(x
))
(
,
(
1
1
x
f
x
))
(
,
n
n
x
f
y
f x
( )
P x f x
( , ( ))
x
X
Y
f x
( )
x
0
f (0)
Jeżeli liczba zero należy do dziedziny funkcji f , to punkt
o współrzędnych
)
0
(
,
0
f
y
x
jest punktem przecięcia się
wykresu z osią OY.
Rzędne punktów przecięcia się wykresu z osią OX są
równe 0
y
ązują
, odcięte (miejsca zerowe funkcji) otrzymujemy
rozwi
c równanie
0
)
(
x
f
.
Rys. 1.
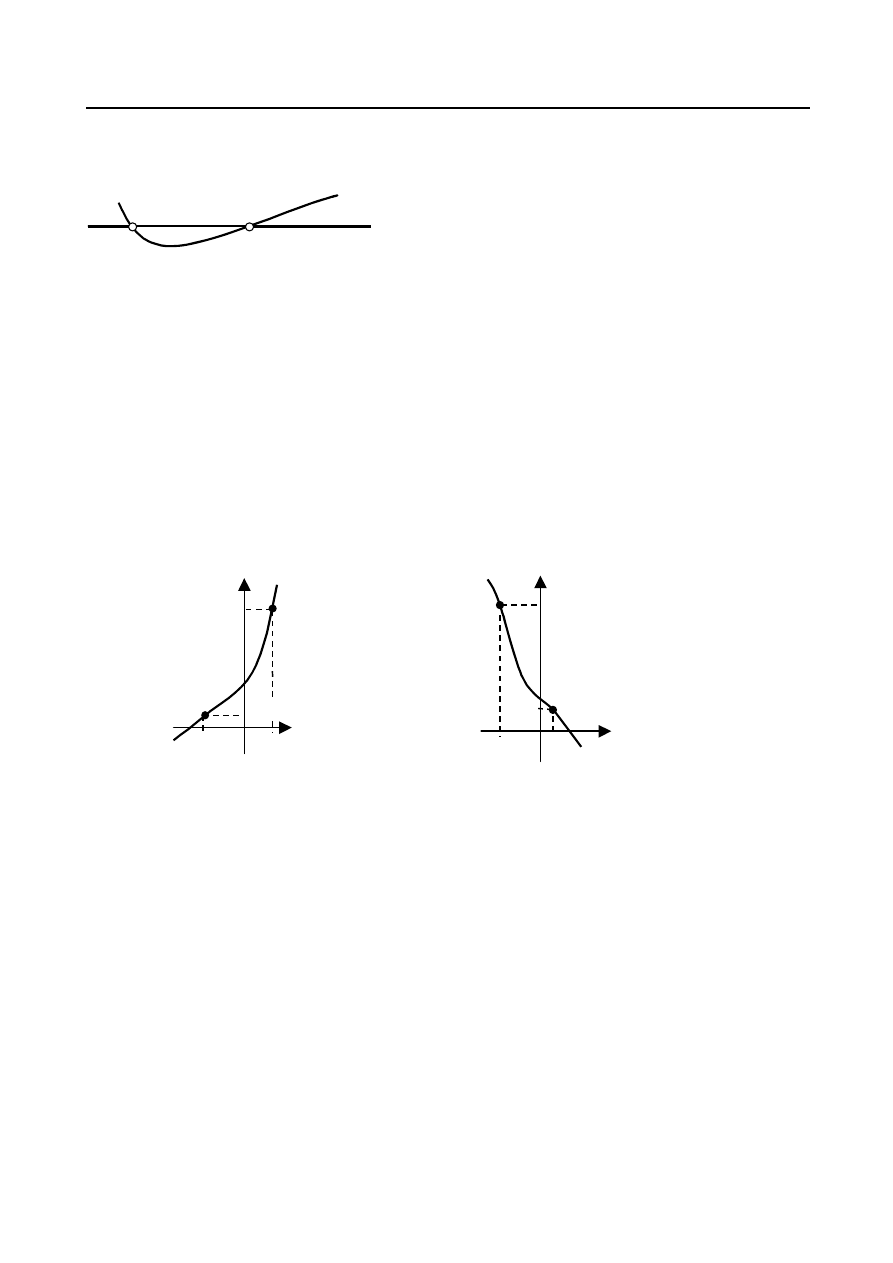
Wykład 7. Funkcje. Podstawowe określenia i własności
2
Szkic wykresu funkcji
)
(x
f
y
w wielu przypadkach
stanowi podstawę do określenia zbioru rozwiązań
,
0
nierówności: 0
)
(
)
(
,
0
)
(
x
x
f
f
bądź
0
)
(
x
f
x
f
(nawet jeżeli uwzględniono na nim jedynie położenie
w
odczytujemy rozwiązanie nierównoś
Rys. 2.
. Niektóre własności funkcji liczbowych
snącą
rostem argum
się
)
(x
f
y
)
;
(
)
;
(
0
)
(
b
a
x
x
f
a
X
b
+ +
+
– –
zględem osi OX).
Na rys.2. przedstawiona została sytuacja, w której
ci 0
)
(
x
f
.
2
Niech
Y
X
f
:
będzie funkcją odwzorowującą pewien zbiór X w zbiór liczb rzeczywistych R.
Funkcję nazywać będziemy ro
w zbiorze X
, jeżeli wraz ze wz
entów zwiększają
wartości funkcji, tj. warunek:
2
1
x
x
pociąga za sobą nierówność
)
(
)
(
2
1
x
f
x
f
dla każdej pary
argumentów
1
x ,
2
x ze zbioru X. Podobnie, funkcję nazywamy maleją
biorze X
, jeżeli wraz ze
mentów zmniejszają się warto
cą w z
2
1
x
x
wzrostem
ści funkcji, tj. warunek:
argu
pociąga za sobą nierówność
żdej pary
entów
ze zbioru X.
ojęcia te zostały zilustrowane na rys.3.
)
(
2
x
f
dla ka
)
(
1
x
f
argum
1
x ,
2
x
P
Y
O
X
funkcja rosnąca
y
f x
( )
x
1
x
2
f x
( )
2
f x
( )
1
)
(
)
(
2
1
x
f
x
f
Y
O
X
funkcja malejąca
y
f x
( )
x
1
x
2
f x
( )
1
f x
( )
2
)
(
)
(
2
1
x
f
x
f
Rys. 3.
notoniczną
, jeżeli w całej swojej dziedzinie jest rosnąca lub w całej
ę nazywamy przedziałami monotoniczną, jeżeli jest w pewnych przedziałach rosnąca, malejąca
b stała.
Funkcję nazywamy (ściśle) mo
swojej dziedzinie jest malejąca.
Funkcj
lu
Przykład 2.
Zbadać monotoniczność funkcji danej wzorem: a)
5
(
3
)
x
x
f
, b)
2
)
(
x
x
f
.
) Funkcja jest rosnąca w zbiorze R po
x
Rozwiązanie. a
nieważ warunek
2
1
x
pociąga za sobą nierówność
ypadku post
)
(
)
(
2
1
x
f
x
f
przyjmującą w tym w
ać
5
3
5
3
2
1
x
x
.
cja jest malejąca w zbiorze
)
0
;
b) Funk
(
1
argumentów
, że )
(
)
(
1
x
f
x
f
X
ponieważ dla
2
1
, x
x
z tego zbioru w
2
1
x
x
po
ierówność
2
2
2
1
x
x
oznacz
że
)
(
)
(
2
1
x
f
x
f
. Funkcja jest rosnąca
w zbiorze
)
X
ponieważ dla
1
x
argumentów
arunek
ciąga za sobą n
ającą,
pociąga za sobą
o
oznaczającą
;
0
(
2
ść
2
2
2
1
x
x
2
, x z tego zbioru warunek
2
1
x
x
nierówn
2
.
Wykład 7. Funkcje. Podstawowe określenia i własności
3
Funkcję
nazywamy różnowartościową w zbiorze X, jeżeli różnym argumentom odpowiadają
różne wartości funkcji, tj. warunek
pociąga za sobą warunek
Y
X
f
:
2
1
x
x
)
(
)
(
2
1
x
f
x
f
dla każdej pary
argumentów ,
ze zbioru X.
1
x
2
x
Uwaga.
Każda funkcja ściśle monotoniczna jest różnowartościowa.
Przykład 3. Zbadać różnowartościowość funkcji danej wzorem
x
x
f
4
)
(
.
Rozwiązanie.
Funkcja jest różnowartościowa w swojej dziedzinie
}
0
{
\
R
D
ponieważ z faktu, że
2
1
x
x
wynika zależność
2
1
4
4
x
x
, czyli
.
)
(
)
(
2
1
x
f
x
f
Niech
będzie funkcją odwzorowującą pewien zbiór X w zbiór liczb rzeczywistych R.
Funkcję tę nazywać będziemy ograniczoną z dołu na zbiorze X , jeżeli wartości funkcji dla argumentów
Y
X
f
:
x X
spełniają warunek
, gdzie m jest pewną liczbą. Podobnie funkcję nazywać będziemy
ograniczoną z góry
na zbiorze X , jeżeli wartości funkcji dla argumentów
m
x
f
)
(
x X
spełniają warunek
, gdzie M jest pewną liczbą.
M
x
f
)
(
W przypadku, gdy funkcja jest ograniczona z dołu i z góry, to nazywamy ją ograniczoną na zbiorze.
Powyższe pojęcia ilustruje rys.4.
Uwaga.
Wykres funkcji ograniczonej z dołu na zbiorze X leży powyżej pewnej prostej poziomej
m
y
,
dla
. Wykres funkcji ograniczonej z góry na zbiorze X leży poniżej pewnej prostej poziomej
X
x
M
y
.
Y
X
y
f x
( )
y=m
O
funkcja ograniczona z dołu
Y
X
y
f x
( )
y=M
O
funkcja ograniczona z góry
Y
X
y
f x
( )
y=M
y=m
O
funkcja ograniczona
Rys. 4.
Zbiór
R
D
nazywamy symetrycznym względem zera, jeżeli warunek
D
x
pociąga za sobą warunek
D
x
)
(
.
Przykład 4.
Jeżeli
, to zbiory
0
a
)
;
;
(
),
;
(
a
a
a
a
są symetryczne względem zera,
a zbiór
a
a
;
(
nie.
Jeżeli zbiór D stanowiący dziedzinę naturalną funkcji f jest symetryczny względem zera oraz
)
(
)
(
x
f
x
f
x
dla każdego
, to funkcję nazywamy parzystą , jeżeli natomiast
dla każdego
, to funkcję nazywamy nieparzystą .
D
x
f
f
)
(
)
(
x
f
x
f
D
Funkcję nazywamy okresową o okresie
f
T
0 , jeżeli warunek
D
x
pociąga za sobą warunek
oraz
dla każdego
D
T
x
)
(
]
)
(
)
(
x
f
T
x
f
D
x
. Najmniejszą liczbę dodatnią T będącą okresem
funkcji okresowej nazywamy okresem podstawowym.
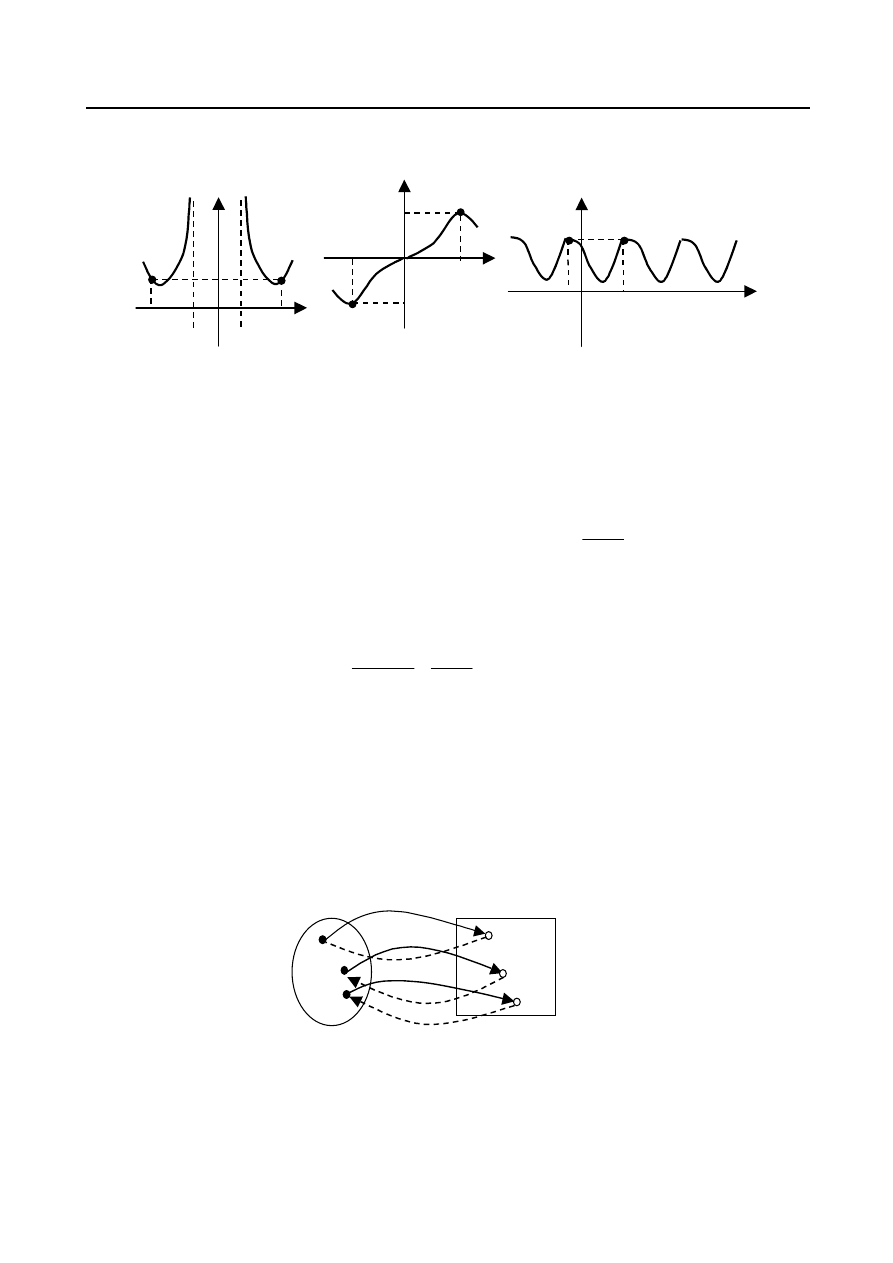
Wykład 7. Funkcje. Podstawowe określenia i własności
4
Wprowadzone
wyżej pojęcia zostały zilustrowane na rys.5.
-
x
x
Y
X
)
(
)
(
x
f
x
f
funkcja parzysta
Y
X
-
x
x
f x
( )
f
x
f x
(
)
( )
funkcja nieparzysta
x+T
Y
X
x
f x
f x T
( )
(
)
funkcja okresowa
Rys. 5.
Uwagi
1. Wykres funkcji parzystej jest symetryczny względem osi OY, funkcji nieparzystej - symetryczny
względem początku układu.
2. Istnieją funkcje, które nie są ani parzyste, ani nieparzyste. Są to funkcje, których wykresy nie spełniają
żadnego z podanych wcześniej warunków.
Przykład 5. Zbadać parzystość funkcji a)
,
b)
x
x
x
f
3
)
(
3
1
)
(
2
2
x
x
x
f
.
Rozwiązanie. a) Dziedziną funkcji jest
, czyli zbiór symetryczny względem zera.
R
D
Ponieważ
) dla każdego
(
)
3
(
)
(
3
)
(
)
(
3
3
x
f
x
x
x
x
x
f
R
x
, to funkcja jest nieparzysta.
b) Dziedziną funkcji jest
)
;
1
(
)
1
;
1
(
)
1
;
(
D
, czyli podzbiór osi liczbowej symetryczny
względem zera. Jednocześnie
)
(
1
1
)
(
)
(
)
(
2
2
2
2
x
f
x
x
x
x
x
f
dla każdego
D
x
. Oznacza to, że
funkcja jest parzysta.
3. Funkcja odwrotna
Niech f będzie funkcją różnowartościową, której dziedziną (niekoniecznie naturalną) jest zbiór X ,
a przeciwdziedziną zbiór Y. Wówczas w zbiorze Y, można w naturalny sposób, określić funkcję
przyporządkowującą każdemu
y Y
ten jedyny
X
x
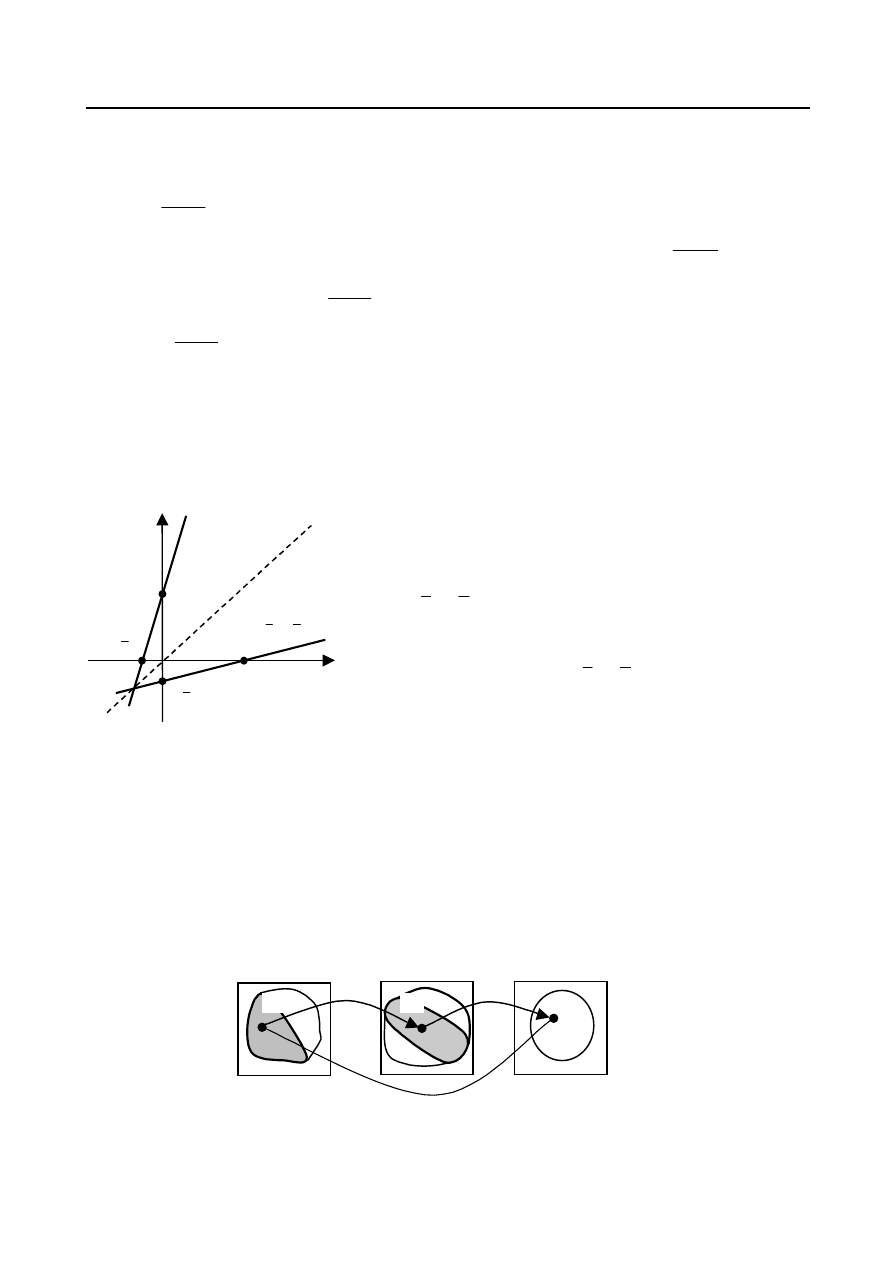
, któremu funkcja f przyporządkowała y (rys.6).
Otrzymaną w ten sposób funkcję nazywamy funkcją odwrotną do funkcji f i oznaczamy symbolem
.
1
f
Tak więc, jeżeli
to
oraz gdy
Y
X
f
:
,
X
Y
f
:
1
y
x
f
)
(
, to
.
x
y
f
)
(
1
X
Y
1
f
f
Rys. 6.
Uwaga.
Funkcję odwrotną najczęściej zapisuje się w postaci
. Zapis ten dostosowany jest do
pewnej tradycji matematycznej, w której przyjęło się argumenty funkcji oznaczać przez x, a wartości funkcji
przez y. W praktyce oznacza to, że aby znaleźć wzór funkcji odwrotnej do funkcji danej wzorem
)
(
1
x
f
y
)
(x
f
y
(o ile funkcja odwrotna istnieje) należy we wzorze
)
(x
f
y
zamienić ze sobą zmienne x i y, a następnie
otrzymane równanie
rozwiązać względem y (albo najpierw rozwiązać równanie
względem x , a potem zamienić zmienne).
)
( y
f
x
)
(x
f
y
Wykład 7. Funkcje. Podstawowe określenia i własności
5
Przykład
6. Wyznaczyć w postaci
funkcję odwrotną do funkcji danej wzorem
)
(
1
x
f
y
3
4
2
)
(
x
x
x
f
y
.
Rozwiązanie. Zamieniając zmienne we wzorze danej funkcji otrzymujemy równanie
3
4
2
y
y
x
, którego
rozwiązaniem względem y jest
2
4
3
x
x
y
. Zatem funkcja odwrotna określona jest wzorem
2
4
3
)
(
1
x
x
x
f
y
. Zauważmy, że dziedziną danej funkcji, a tym samym przeciwdziedziną odwrotnej jest
, natomiast przeciwdziedziną danej, czyli dziedziną odwrotnej jest
.
}
3
(
\
R
D
}
2
(
\
1
R
D
Przykład
7. Wyznaczyć w postaci
funkcję odwrotną do funkcji
)
(
1
x
f
y
2
3
)
(
x
x
f
y
.
Sporządzić na jednym rysunku wykresy obu funkcji.
Rozwiązanie. Dana funkcja jest funkcją różnowartościową o dziedzinie
R
X
i przeciwdziedzinie
R
Y
.
Funkcja posiada więc funkcje odwrotną .
y
x
3
2
y
x
y
x
1
3
2
3
X
Y
2
2
3
2
3
2
Rys. 7.
Zamieniając zmienne we wzorze danej funkcji otrzymujemy
równanie 2
3
y
x
, którego rozwiązaniem względem y
jest
3
2
3
x
.
1
y
Oznaczając otrzymaną funkcję przez
otrzymujemy
f
x
1
( )
3
2
3
1
)
(
1
x
y
x
f
.
Wykresy obu funkcji przedstawione zostały na rys.7.
Uwaga. Wykresy funkcji odwrotnych są symetryczne względem prostej
x
y
.
4. Funkcje złożone
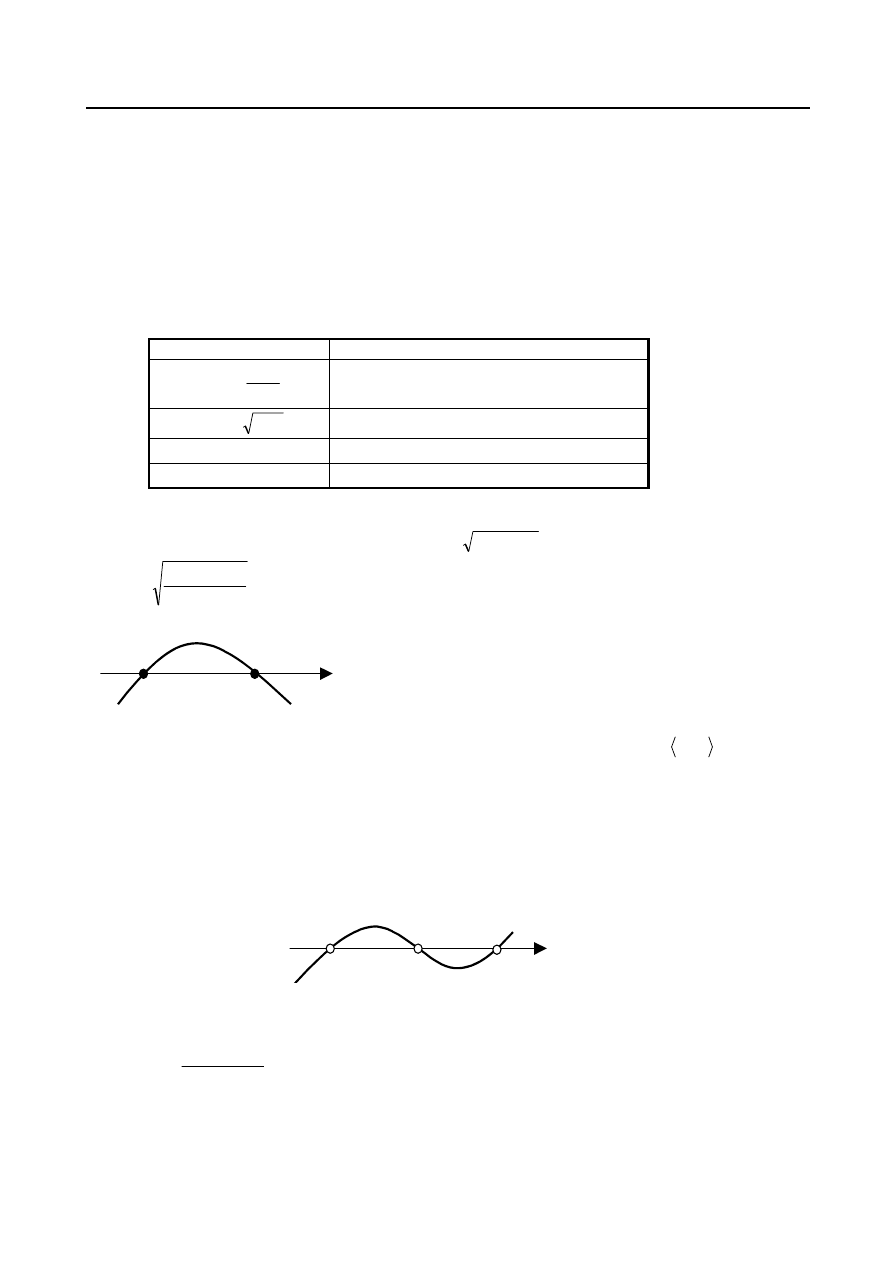
Niech
(patrz rys.38.) przy czym zbiór
R
U
g
R
X
f
:
,
:
}
)
(
:
{
0
U
x
f
X
x
X
jest niepusty.
Na zbiorze
można z pomocą funkcji f i g określić funkcję wzorem:
0
X
))
(
(
)
(
x
f
g
x
h
. Tę nową funkcję
nazywać będziemy złożeniem funkcji g i f i oznaczać symbolem
. Tak więc
f
g
))
(
(
)
)(
(
)
(
x
f
g
x
f
g
x
h
.
0
X
U
X
R
R
R
x
u
y
f
g
f
g
h
Rys. 8.
Uwaga.
Aby obliczyć należy argument we wzorze funkcji g zastąpić wyrażeniem .
))
(
(
x
f
g
)
(x
f
Wykład 7. Funkcje. Podstawowe określenia i własności
6
Przykład 8.
Niech
będą funkcjami określonymi wzorami:
,
. Wyznaczyć funkcje
f R
R g R
R
:
,
:
g
f
f
g
)
3
)
(
2
x
x
f
x
x
x
g
cos
)
(
f
f
,
,
.
Rozwiązanie.
,
3
cos(
)
3
(
)
3
(
))
(
(
)
)(
(
2
2
2
x
x
x
g
x
f
g
x
f
g
3
cos
)
cos
(
))
(
(
)
)(
(
2
2
x
x
x
x
f
x
g
f
x
g
f
,
.
3
)
3
(
)
3
(
))
(
(
)
)(
(
2
2
2
x
x
f
x
f
f
x
f
f
Przy wyznaczaniu dziedziny funkcji złożonej należy zapewnić spełnienie m.in. następujących warunków:
Postać funkcji
Warunek wyznaczający dziedzinę
)
(
)
(
)
(
x
u
x
p
x
f
0
)
(
x
u
)
(
)
(
x
u
x
f
0
)
(
x
u
)
(
log
)
(
x
u
x
f
a
0
)
(
x
u
)
(
arcsin
)
(
x
u
x
f
1
)
(
1
x
u
Przykład 9.
Wyznaczyć dziedzinę funkcji: a)
x
x
x
f
4
)
(
2
, b)
,
)
2
3
ln(
)
(
2
3
x
x
x
x
f
c)
2
2
)
(
2
x
x
x
x
f
.
Rozwiązanie.
0
4
X
)
4
(
x
x
y
_
+ +
_ _
Rys. 9.
) Funkcja jest określona, gdy wyrażenie logarytmowane jest dodatnie. Zatem
ewej stronie tej nierówności
u przedstawia rys.10. Na jego podstawie stwierdzam
a) Wzór określający funkcję ma sens, gdy wyrażenie
podpierwiastkowe jest nieujemne.
:
{
R
x
D
f
Rozwiązując nierówność otrzymuje
wykresu trójmianu występującego po lewej stronie tej
nierówności przedstawia rys.9. Stąd
}
0
4
2
x
x
.
my
0
)
4
(
x
x
. Szkic
4
;
0
f
D
.
b
}
0
2
3
:
{
2
3
x
x
x
R
x
D
f
. Rozkładając na czynniki występujący po l
)
2
)(
1
(
)
2
3
(
2
3
)
(
2
2
3
x
x
x
x
x
x
x
x
x
x
W
.
Szkic wykresu tego wielomian
y, że
wielomian dostajemy kolejno
)
;
2
(
)
1
;
0
(
f
D
.
0
1
2
X
y W x
( )
+
_ _
+
_ _
Rys. 10.
c) Z określenia pierwiastka kwadratowego wynika, że wyrażenie podpierwiastkowe jest nieujemne,
z określenia funkcji wymiernej, że mianownik jest różny od zera. Zatem
}
0
2
0
2
2
2
x
x
Pierwiastkami jednokrotnym
2
,
1
2
1
;
{
x
x
R
x
D
. Otrzymany układ nierówności jest w zbiorze
równoważny nierównoś
. Lewa strona tej nierówności jest wielom
}
2
{
\
R
ianem .
ci: 0
)
2
)(
2
(
2
x
x
x
i tego wielomianu są:
x
x
oraz
2
3
x
. Na tej podstawie
sporządzamy szkic wykresu przedstawiony na rys.11.
Wykład 7. Funkcje. Podstawowe określenia i własności
7
-
2
1
2
X
y W x
( )
+
_ _ _
+
_ _
Zbiorem rozwiązań nierówności, a tym samym
dziedziną funkcji jest
.
)
2
;
1
2
;
(
f
D
Rys. 11.
5. Przekształcenia wykresów funkcji
Wykres funkcji powstaje z wykresu funkcji
)
(x
f
y
przez
)
(
a
x
f
y
przesunięcie o wektor
(przesunięcie wzdłuż osi OX o a jednostek)
]
0
,
[ a
A
x
f
y
)
(
przesunięcie o wektor
(przesunięcie wzdłuż osi OY o A jednostek)
]
,
0
[
A
)
( x
f
y
symetryczne odbicie względem osi OY
)
(x
f
y
symetryczne odbicie względem osi OX
)
(x
f
y
symetryczne odbicie względem osi OX tej części wykresu funkcji
, która
leży poniżej osi OX i pozostawieniu bez zmian tej części, która leży powyżej.
)
(x
f
y
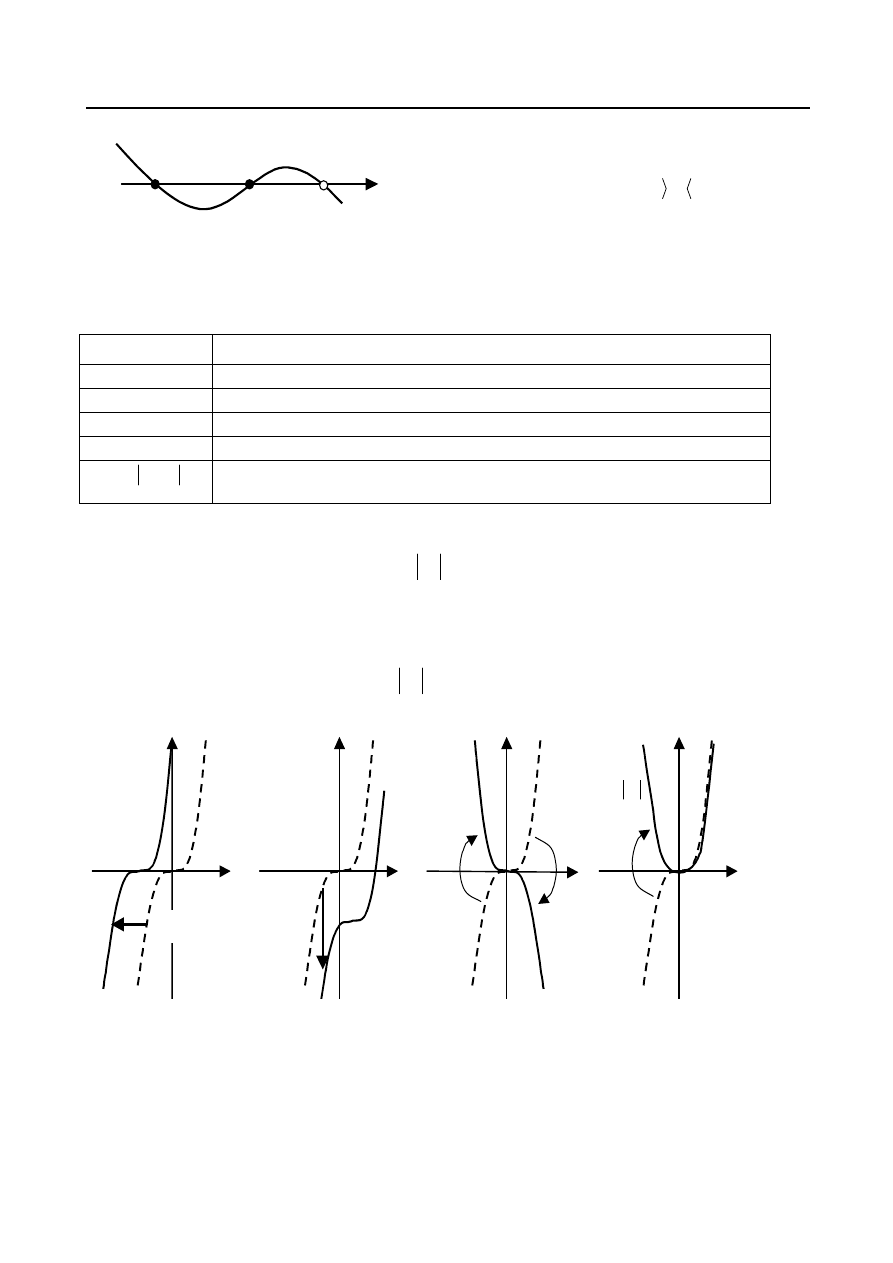
Przykład 10.
Dokonując odpowiedniego przekształcenia wykresu funkcji
naszkicować wykresy
funkcji:
,
,
,
3
x
y
3
)
2
(
x
y
3
3
x
y
3
x
y
3
x
y
.
Rozwiązanie.
Linią przerywaną na rys.12. naszkicowano wykres danej funkcji
. Wykres funkcji
powstał z wykresu danej przez przesunięcie wzdłuż osi OX o 2 jednostki w lewo, wykres
funkcji przez przesunięcie w dół o 3 jednostki, wykres funkcji
przez symetryczne
odbicie względem osi OX, wykres funkcji
3
x
y
3
x
3
)
2
(
x
y
x
y
3
3
y
3
x
y
przez symetryczne odbicie względem osi OX tej części
wykresu danej funkcji, która leżała poniżej osi OX i pozostawieniu bez zmian tej części, która znajdowała
się powyżej.
]
0
;
2
[
u
–2
8
3
)
2
(
x
y
X
Y
]
3
;
0
[
u
–3
X
Y
3
3
x
y
X
Y
3
x
y
X
Y
3
x
y
Rys. 12.
Document Outline