Tomasz Kowalski

Wykłady z matematyki dla studentów kierunków ekonomicznych

Wykład 14

ZASTOSOWANIA RACHUNKU RÓŻNICZKOWEGO

FUNKCJI JEDNEJ ZMIENNEJ W EKONOMII – lista zadań

1. Zbadać funkcję

x

b

a

e

y





,

0

,



b

a

, i naszkicować jej wykres. Funkcja ta opisuje zależność popytu na

dobra konsumpcyjne od wielkości dochodu konsumenta.

2. Całkowity koszt w złotych wyprodukowania w małej fabryce w ciągu tygodnia x artykułów dany jest

wzorem:

2

100

1

5

50

)

(

x

x

x

K







. Obliczyć

)

25

(

)

26

(

K

K



i porównać z

)

25

(

/

K

.

3. Obliczyć elastyczność funkcji

6

3

)

(



 x

x

f

.

4. Koszt )

(x

K

wyprodukowania w ciągu dnia x foteli wynosi

36

5

. Podać koszt przecięt-

ny i koszt krańcowy. Zbadać dla jakiego x koszt przeciętny jest minimalny. Naszkicować wykres kosz-
tu przeciętnego i kosztu krańcowego.

)

(

2







x

x

x

K

5. Obliczyć elastyczność funkcji

5

2

i naszkicować jej wykres (dla

0



x

).

)

(

2







x

x

x

f

6. Producent chce sprzedać zupę w cylindrycznych puszkach, przy czym w puszce ma się zmieścić

oraz puszka ma być wykonana z arkusza blachy o minimalnym polu. Jakie wymiary powinny mieć te
puszki?

3

cm

54



7. Konkurent producenta z poprzedniego zadania decyduje się sprzedawać zupę również w cylindrycznych
puszkach, przy czym na wykonanie puszki przeznacza

blachy, a wymiary puszki są takie, że

ma ona największą objętość. Jakie to wymiary?

2

cm

24



8. W badaniach prognostycznych wykorzystywana jest tzw. funkcja Gompertza

, gdzie

oznaczają pewne stałe dodatnie i dodatkowo

x

c

ab

y



a b c d

, , ,

1

,

1





c

b

. Naszkicować następujące funkcje tego rodzaju:

a)

, b)

x

y

4

2

3





x

y

3

)

5

4

(

5





, c)

x

y

)

2

1

(

3

10





, d)

x

y

)

2

1

(

)

3

2

(

4





.

Odpowiedzi

1. Ze względu na istotę zagadnienia

)

;

0

(







D

.

a

. Prosta

a

e

y



jest

asymptotą poziomą prawostronną .

x

x

e

x

f

x

f













)

(

lim

,

0

)

(

lim

0

x

b

ax

e

x

b

. Funkcja rośnie w zbiorze D.

x

f





2

/

)

(

x

b

ax

e

x

b

x

b

x

f









4

//

)

2

(

)

(

a

e

y



2

b

2



a

e

X

Y

x

b

ax

e

y





. Funkcja jest wypukła

w przedziale

)

2

;

0

(

b

)

;

2

(





b

i wklęsła w przedziale

.

Punkt

)

,

2

(

2



a

e

b

P

jest punktem przegięcia.

Zastosowania rachunku różniczkowego w ekonomii – lista zadań

2

2. Mamy tutaj

49

,

4

)

. Ponieważ

25

(

)

26

(



 K

K

x

x

K

50

1

5

)

(

/





, to

5

,

4

2

1

5

)

25

(

/







K

. Obie wielko-

ści różnią się nieznacznie.

3.

2

3

6

3

)

(

)

(

)

(

/













x

x

x

x

x

f

x

f

x

x

E

. Tak więc dla

4



x

elastyczność

2

)

4

(



E

. Oznacza to, że jeżeli

wartość x wzrośnie o 1%, to wartość funkcji wzrośnie o około 2%. (Tutaj wzrost argumentu funkcji o
1%, tzn. od wartości 4 do wartości 4,04 pociąga za sobą wzrost wartości funkcji od 6 do 6,12 czyli do-
kładnie o 2%).

x

x

x

x

K

x

f

36

5

)

(

)

(









6

)

(

/

x

K

y



)

(x

f

y



Y

X

17

4. Koszt przeciętny

jest minimalny,

gdy

)

(x

E

y



X

Y

2

y

x

 

3 2

4

Y

X

6

5.

Elastyczność

5

2

2

2

)

(

2

2









x

x

x

x

x

E

jest funkcją rosnącą.

6. Jeżeli przyjąć jako x promień podstawy walca, to wysokość walca

2

54

x

h



, a pole powierzchni

x

x

S





108

2

2





. Funkcja ta przyjmuje (w przedziale

)

;

0

(





) wartość najmniejszą gdy

. Warunki

zadania spełnia walec o średnicy 6 cm i wysokości 6 cm (walec, którego przekrój osiowy jest kwadra-
tem).

3



x

7. Jeżeli oznaczyć przez x promień podstawy walca, wówczas wysokość walca

x

x

h

2

12





,

a w konsekwencji V

. Funkcja ta przyjmuje (w przedziale

)

12

(

2

x

x







)

3

2

;

0

(

) wartość najmniejszą

gdy . Warunki zadania spełnia walec, którego przekrój osiowy jest kwadratem.

2



x

8. a) Dla funkcji

, przyjmując

x

x

f

4

2

3

)

(





)

;

0







D

,

mamy:











)

(

lim

,

6

x

f

x

)

0

(

f

.

Funkcja jest rosnąca i wypukła w dół w zbiorze D.

6



x

. Koszt krańcowy .

5

2

)

(

/



 x

x

K

)

6

(

17

)

6

(

/

K

f





.

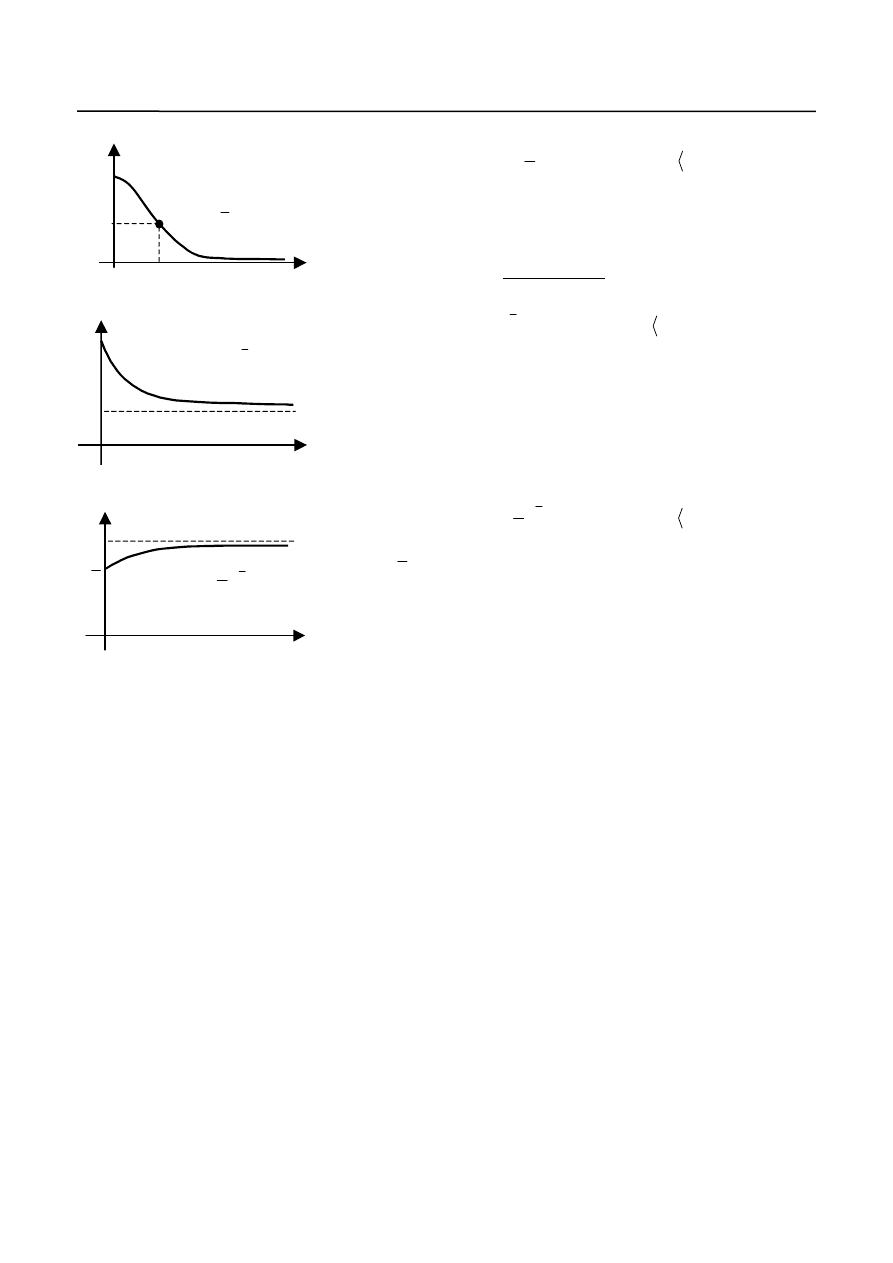
Zastosowania rachunku różniczkowego w ekonomii – lista zadań

3

x

x

f

3

)

5

4

(

5

)

(





t

x

y

3

)

5

4

(

5





Y

X

b) Dla funkcji

, przyjmując

)

;

0







D

,

mamy:

0

)

0

(

)

(

lim

,

4









x

f

x

f

.

4

2

Funkcja jest malejąca w zbiorze D, wypukła w górę w przedziale

oraz wypukła w dół w przedziale

, gdzie

)

;

0

(

t

)

;

(





t

36

,

1

)

4 

3

ln

ln

5

ln(ln







t

.

x

x

f

)

2

c) Dla funkcji

1

(

3

10

)

(





, przyjmując

)

;

0







D

, mamy:

10

)

(

lim

,

30

)

0

(









x

f

x

f

.

y

x





10 3

1
2

( )

Y

X

10

30

Funkcja jest malejąca i wypukła w dół w zbiorze D.

d) Dla funkcji

x

c

f

)

2

1

(

)

3

2

(

4

)

(





, przyjmując

)

;

0







D

, mamy:

4

)

(

lim







x

f

Y

x

y

)

2

1

(

)

3

2

(

4





X

3

8

4

,

3

8

)

0

(



f

x

.

Funkcja jest rosnąca i wypukła w górę w zbiorze D.