1
Chem. Fiz. TCH II/12
1
Roztwory rzeczywiste (1)
-2000
-1500
-1000
-500
0
500
1000
1500
2000
0
0,2
0,4
0,6
0,8
1
∆
∆
∆
∆G
Τ∆
Τ∆
Τ∆
Τ∆S
∆
∆
∆
∆H
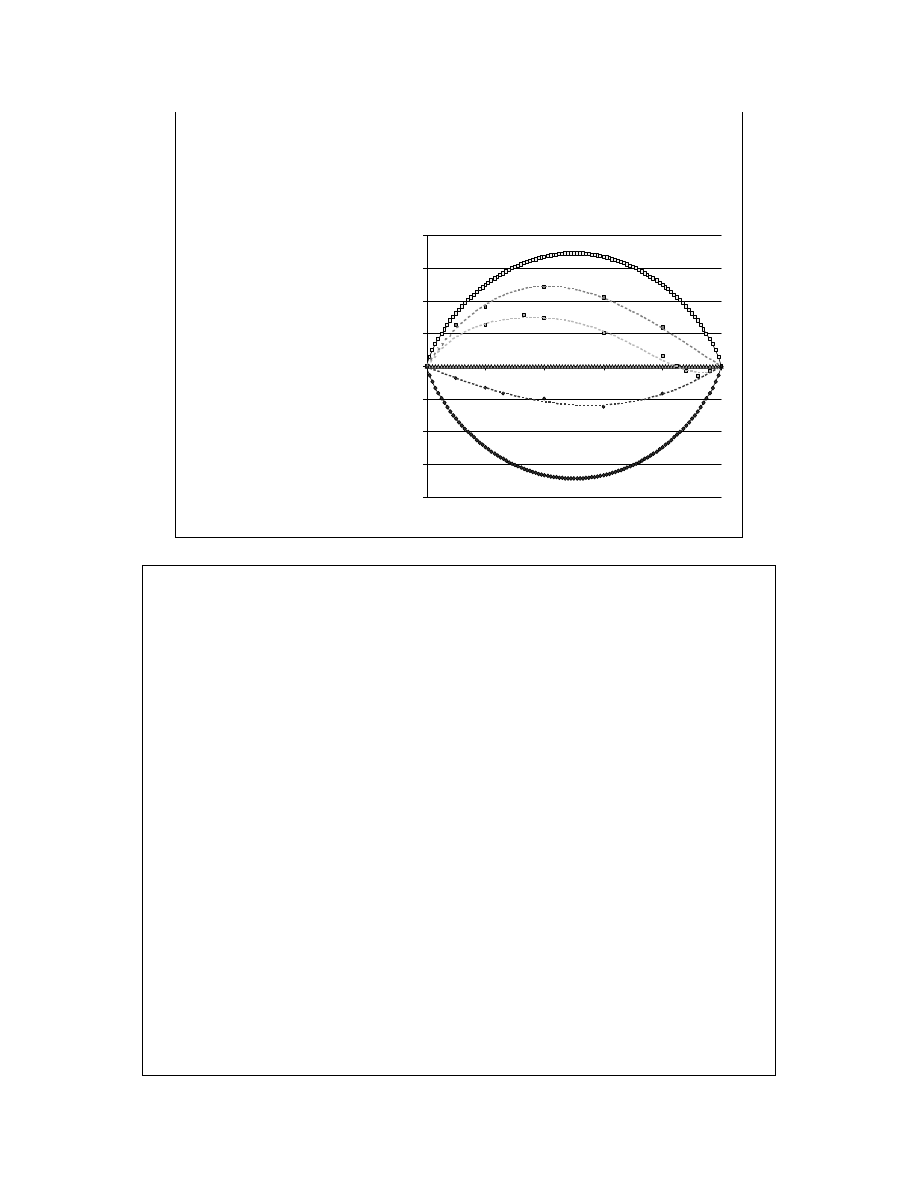
Również w temp. 298,15K,
ale dla CCl
4
(A) i CH
3
OH
(B).
Przyczyny dodatnich i ujemnych odchyleń od prawa Raoulta – konsekwencja
oddziaływań międzycząsteczkowych w roztworze.
Można wyprowadzić całą termodynamikę roztworów doskonałych (także prawo
Raoulta) na gruncie termodynamiki statystycznej, przy założeniach:
1. Odziaływania międzycząsteczkowe AA, BB i AB są w przybliżeniu równe,
2. Objętości molowe A i B są w przybliżeniu równe.
Jeżeli oddziaływania AB są silniejsze od tych AA i BB, to odchylenia powinny być
ujemne (i odwrotnie).
Dodatnie odchylenia obserwuje się przede wszystkim w przypadkach, gdy czyste
substancje tworzą asocjaty (dimery, itp.), które są rozrywane podczas
rozpuszczania. Jest to widoczne na wykresie, gdzie widać endotermiczny
proces rozrywania wiązań wodorowych w metanolu podczas rozcieńczania go
tetrachlorkiem węgla. Entropia mimo wszystko jest nadal spora, lecz w sumie
entalpia swobodna mieszania jest znacznie mniejsza niż dla roztworu
doskonałego.
2
Chem. Fiz. TCH II/12
2
Roztwory rzeczywiste (2)
-2500
-2000
-1500
-1000
-500
0
500
1000
1500
2000
0
0,2
0,4
0,6
0,8
1
∆
∆
∆
∆G
Τ∆
Τ∆
Τ∆
Τ∆S
∆
∆
∆
∆H
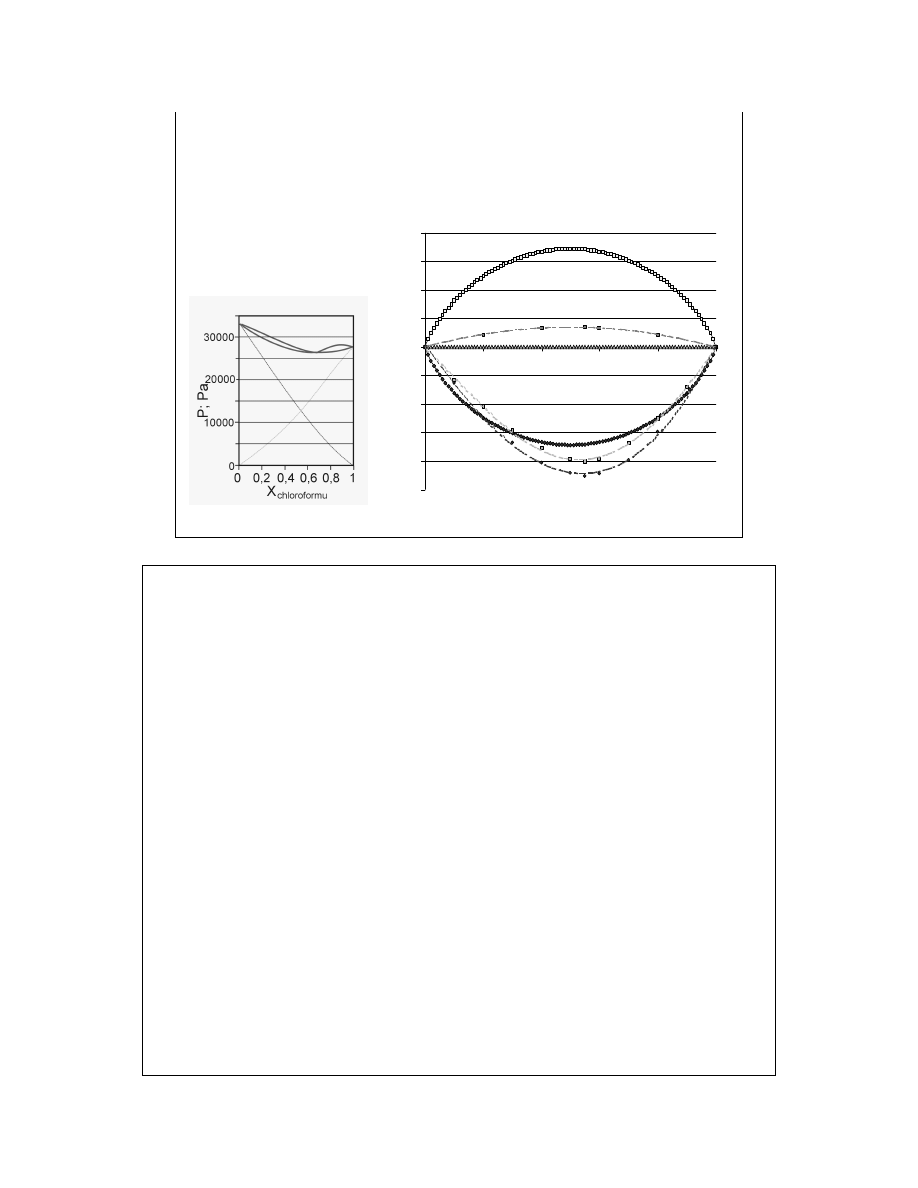
Tym razem dla (CH
3
)
2
CO
(A) i CHCl
3
(B).
Oba te związki tworzą słabe wiązania wodorowe (niewielkie odchylenia ujemne),
obniżenie entropii mieszania (znaczne), entalpia swobodna zmienia się niewiele,
bowiem jest jednak wyraźny efekt cieplny (kompensujący małą zmianę entropii).
Jest to klasyczne współdziałanie efektu entalpowego i entropowego.
3
Chem. Fiz. TCH II/12
3
Funkcje nadmiarowe
-2500
-2000
-1500
-1000
-500
0
500
0
0,2
0,4
0,6
0,8
1
G
E
Τ∆
Τ∆
Τ∆
Τ∆S
E
H
E
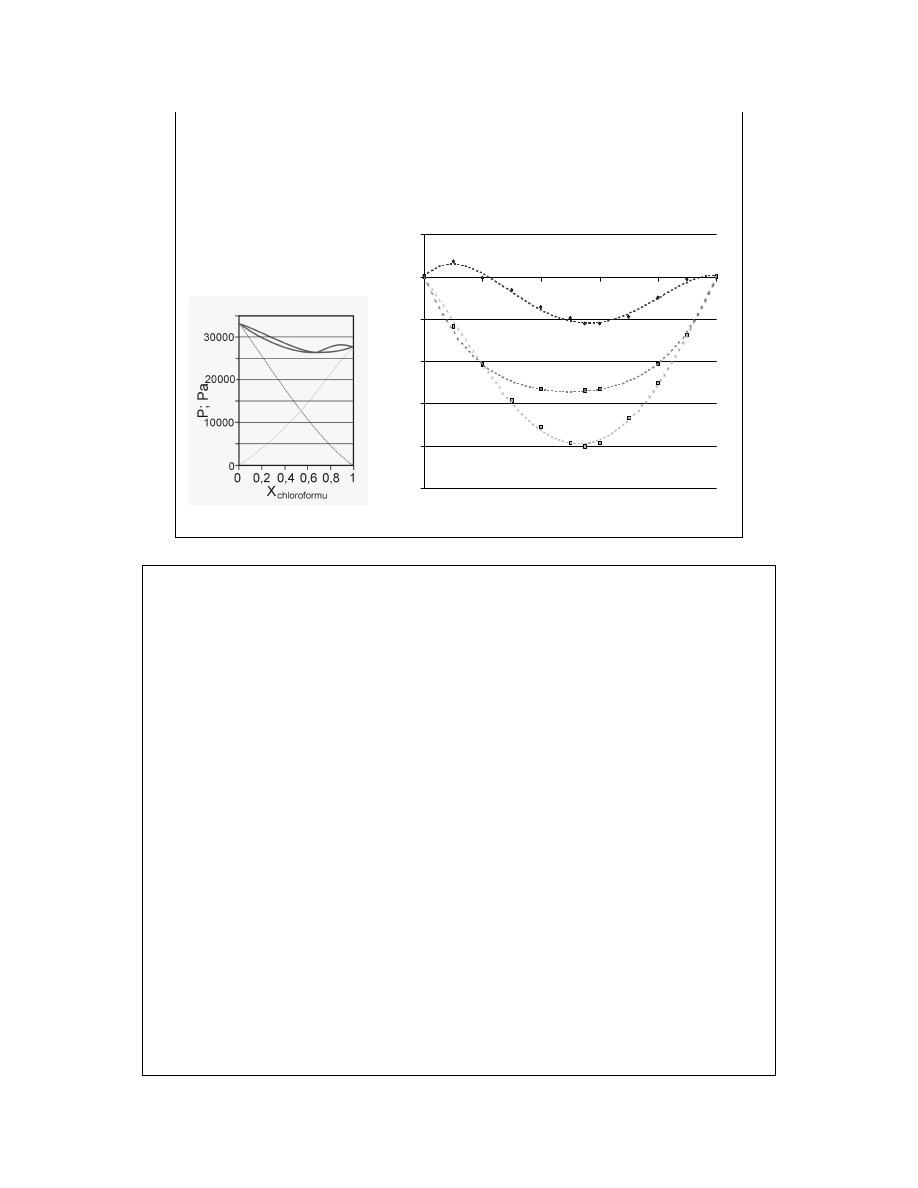
Ponownie dla (CH
3
)
2
CO
(A) i CHCl
3
(B).
Pojęcie roztworu prawidłowego (regularnego), tj. takiego, dla którego H
E
≠0, lecz
S
E
=0.
Np., pięknie można zobaczyć kontrakcję na wykresie V
E
.
4
Chem. Fiz. TCH II/12
4
Roztwory rzeczywiste (3)
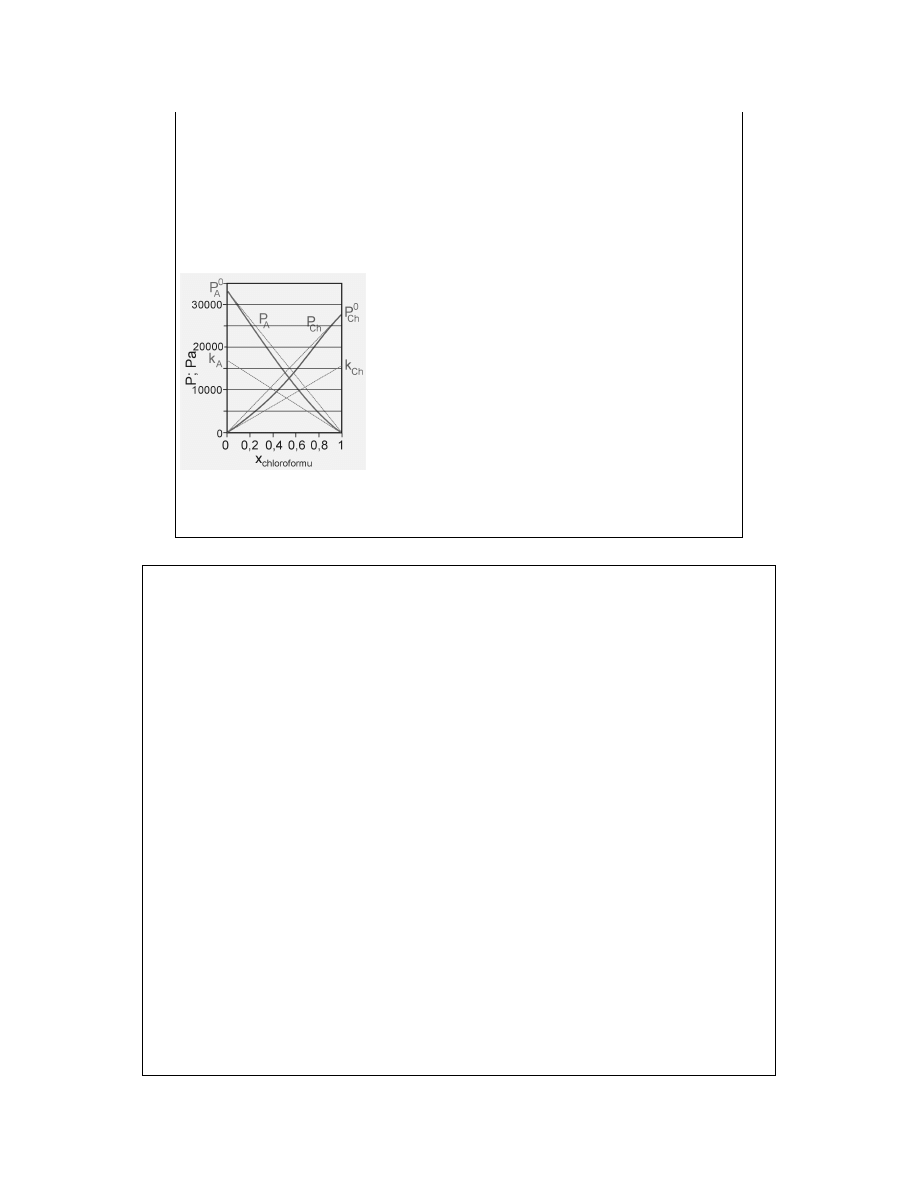
Bez względu na przyczyny odchyleń można zaobserwować, że:
1. dla x
i
→
→
→
→
1
P
i
→
→
→
→
P
0
i
·x
i
(prawo Raoulta)
2. dla x
i
→
→
→
→
0
P
i
→
→
→
→
k
i
·x
i
(prawo Henry’ego)
Roztwór, którego składniki spełniają obie
w/w prawidłowości nosi nazwę roztworu
doskonale rozcieńczonego.
Rozpuszczalnik – prawo Raoulta
Substancja rozpuszczona – prawo Henry’ego.
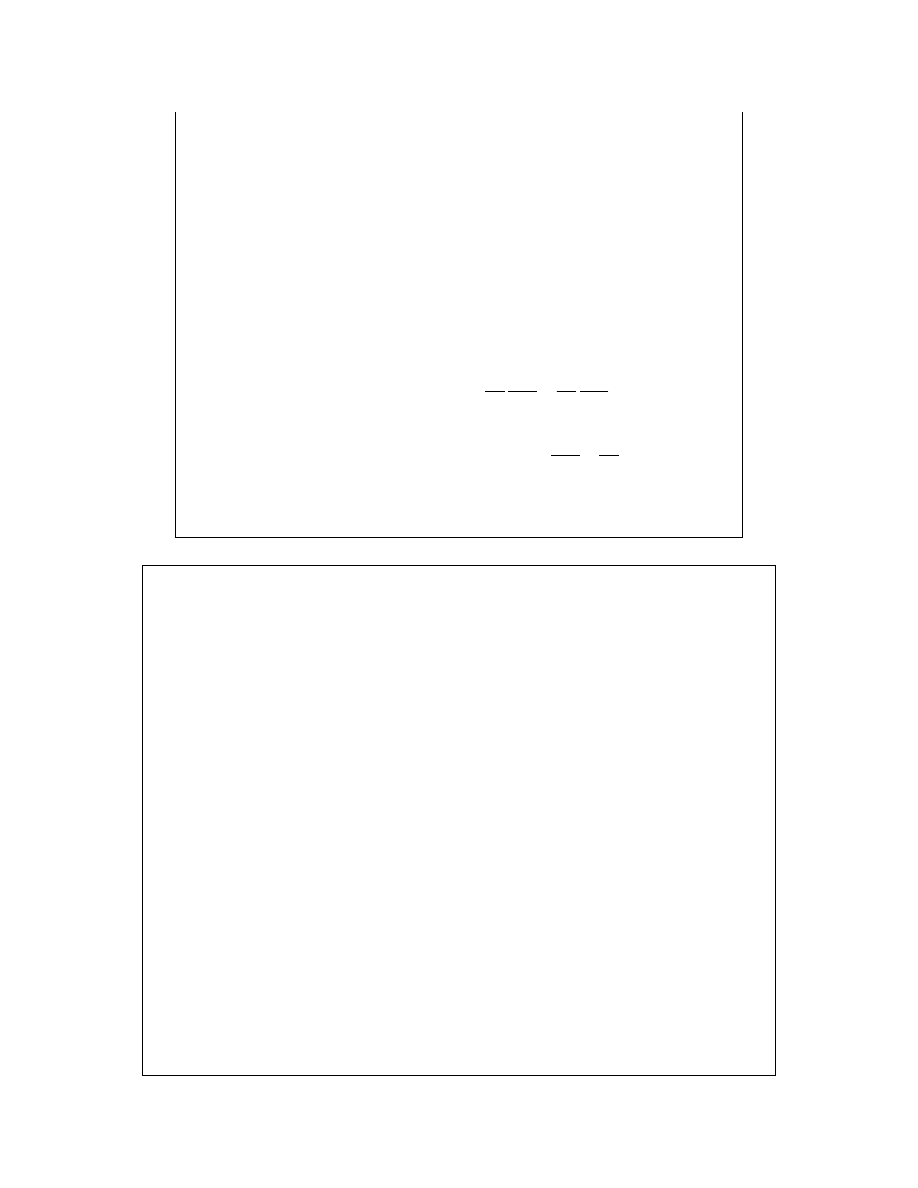
5
Chem. Fiz. TCH II/12
5
Roztwory rzeczywiste (4)
Jeśli rozpuszczalnik spełnia prawo Raoulta, to jest termodynamiczną
koniecznością, aby substancja rozpuszczona spełniała prawo Henry’ego.
Ponownie wychodzimy z równania Gibbsa-Duhema, zapisując je:
0
ln
ln
=
+
B
B
A
A
P
d
x
P
d
x
co po przekształceniu i obustronnym podzieleniu przez dx
A
=–dx
B
daje:
B
B
A
A
P
d
x
P
d
x
ln
ln
−
=
B
B
B
B
A
A
A
A
dx
dP
P
x
dx
dP
P
x
=
B traktujemy jako substancję
rozpuszczoną, zatem:
B
B
x
k
P
⋅
=
i
B
B
B
B
x
P
dx
dP
k
=
=
Ta forma równania Gibbsa-Duhema została uzasadniona w wykładzie 11 – slajd
„Roztwory doskonałe (idealne)”.
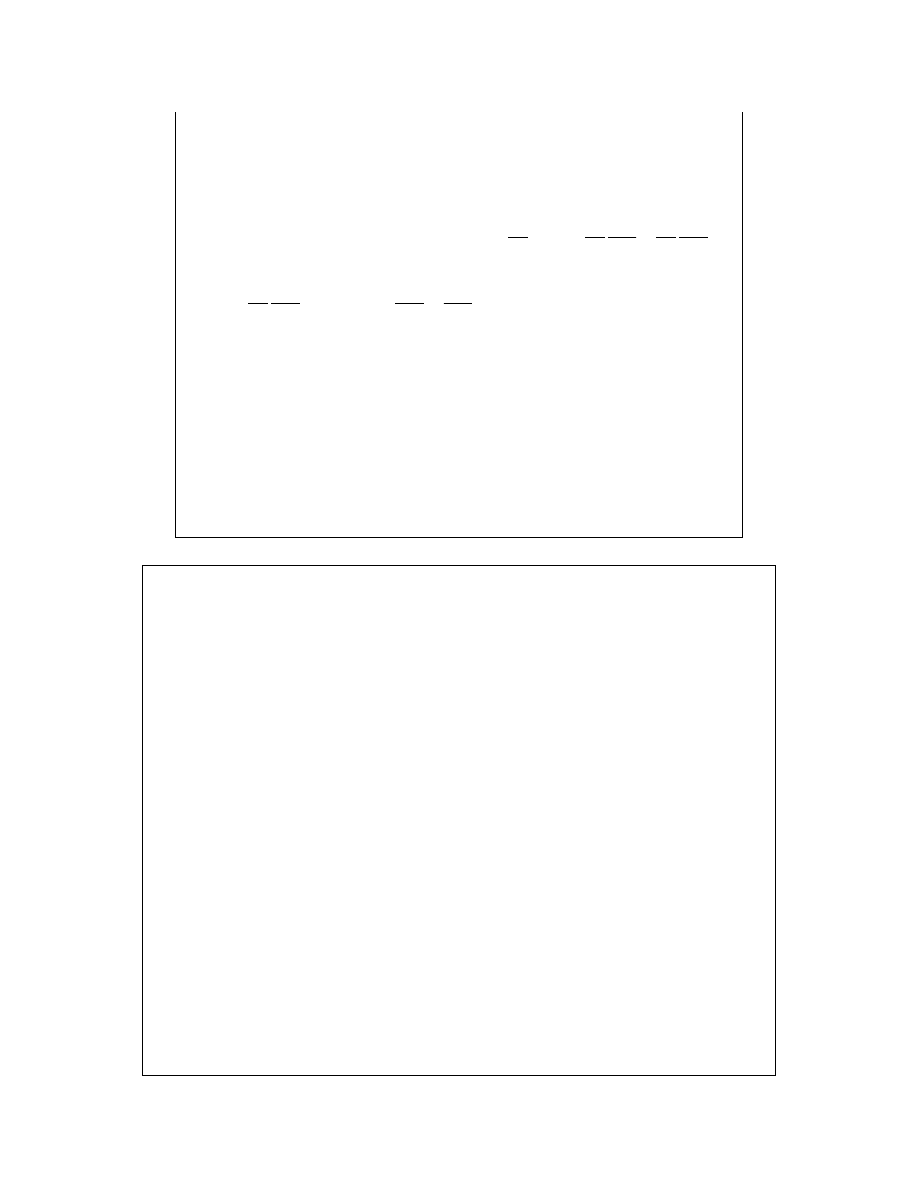
6
Chem. Fiz. TCH II/12
6
Roztwory rzeczywiste (5)
Podstawienie znalezionej zależności:
B
B
x
P
k
=
do
B
B
B
B
A
A
A
A
dx
dP
P
x
dx
dP
P
x
=
Daje:
1
=
A
A
A
A
dx
dP
P
x
oraz:
A
A
A
A
x
dx
P
dP
=
co po scałkowaniu wygląda tak:
const
x
P
A
A
+
= ln
ln
a po skorzystaniu z warunku brzegowego:
gdy:
1
=
A
x
to:
0
A
A
P
P
=
otrzymujemy:
0
ln
A
P
const
=
i ostatecznie:
0
ln
ln
ln
A
A
A
P
x
P
+
=
0
A
A
A
P
x
P
=
czyli
QED
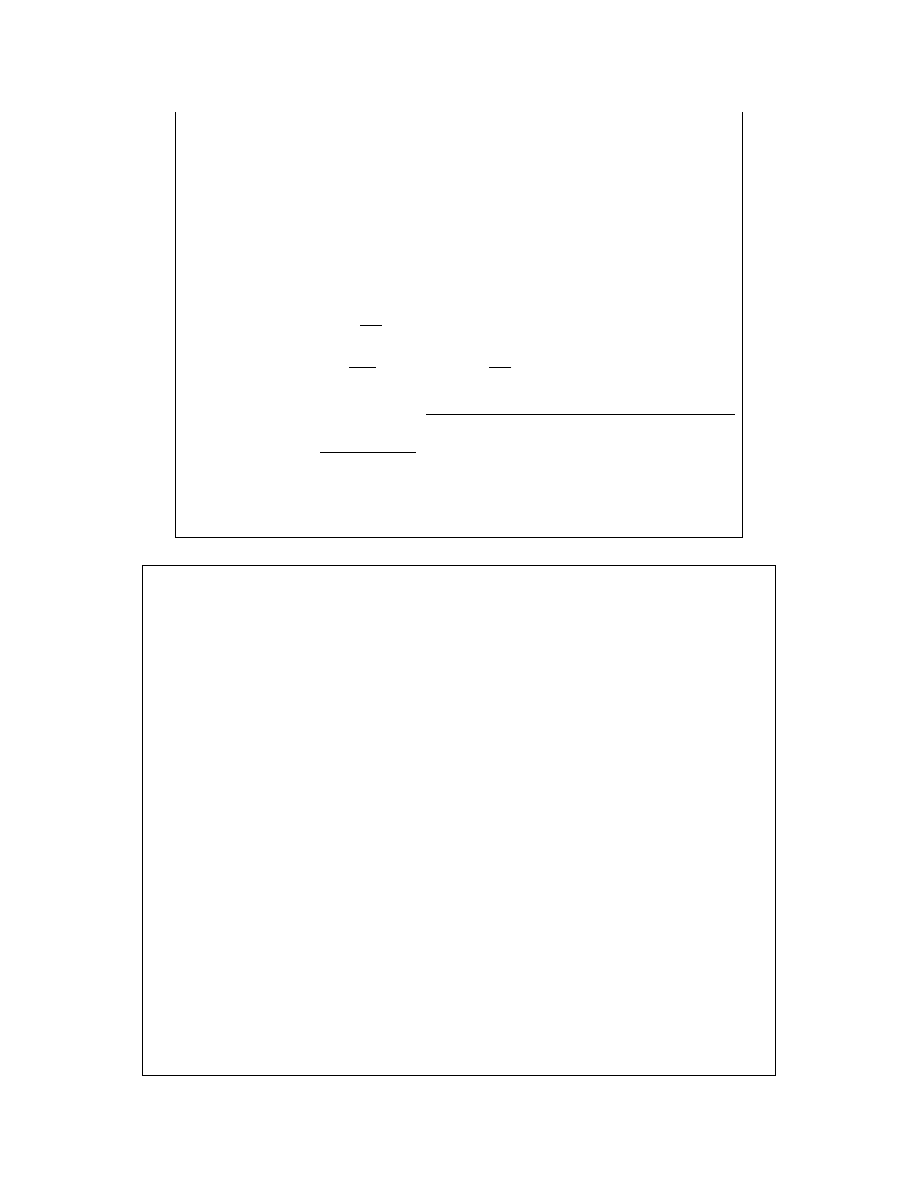
7
Chem. Fiz. TCH II/12
7
Potencjały chemiczne w
roztworach rzeczywistych
Dla rozpuszczalnika już znamy:
A
A
A
x
RT
ln
0
+
=
µ
µ
Dla substancji rozpuszczonej korzystamy znów z faktu, że jest w
równowadze ze swoimi parami, kiedy to:
a po uwzględnieniu prawa Henry’ego:
0
0
,
ln
P
P
RT
B
g
B
B
+
=
µ
µ
B
B
B
g
B
B
g
B
B
x
RT
x
RT
P
k
RT
P
kx
RT
ln
ln
ln
ln
0
0
,
0
0
,
+
=
+
+
=
+
=
⊗
µ
µ
µ
µ
gdzie wielkość:
⊗
B
µ
zwana jest standardowym potencjałem chemicznym
Jest to wielkość hipotetyczna, odpowiadałaby bowiem potencjałowi
składnika B dla x
B
=1, gdyby równanie było spełnione (jak i prawo
Henry’ego) aż do tej wartości.
Odnośnie pierwszego równania dla substancji rozpuszczonej – patrz slajd
„Potencjały chemiczne” w wykładzie 11.
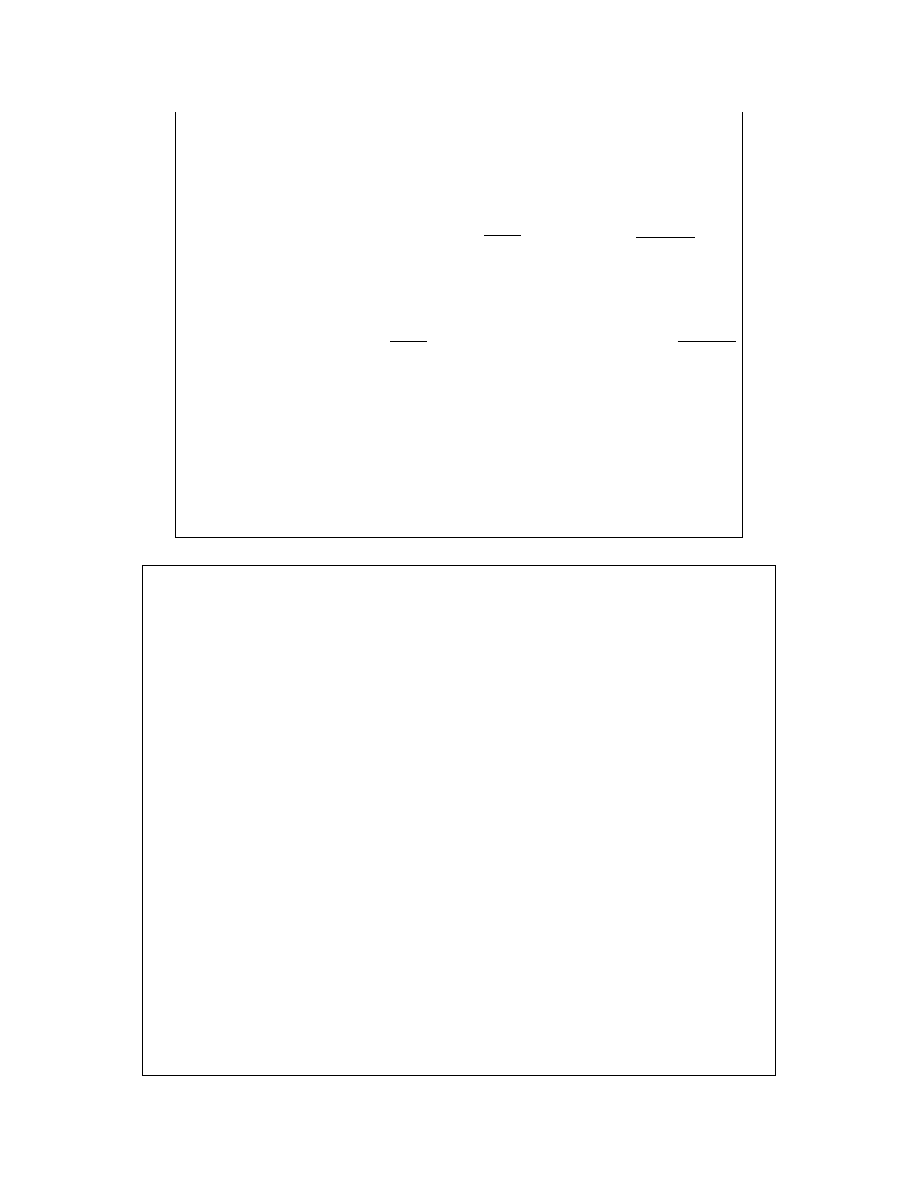
8
Chem. Fiz. TCH II/12
8
Standardowe potencjały
chemiczne
Uwzględniając znane zależności:
B
A
B
m
M
x
1000
=
oraz:
B
A
A
B
c
M
x
ρ
1000
=
Możemy zapisać:
B
B
m
B
m
RT
ln
+
=
⊗
µ
µ
oraz:
B
B
c
B
c
RT
ln
+
=
⊗
µ
µ
gdzie:
1000
ln
A
B
B
m
M
RT
+
=
⊗
⊗
µ
µ
A
A
B
B
c
M
RT
ρ
µ
µ
1000
ln
+
=
⊗
⊗
Standardowe potencjały chemiczne w skali molalności i stężenia
molowego są także wielkościami hipotetycznymi, które przyjmowałby
potencjał chemiczny składnika B dla wartości m=1 lub c=1, gdyby
prawo Henry’ego obowiązywało aż do tych wartości.
Zależności te, słuszne dla roztworów rozcieńczonych wyprowadzane były m.in. w
wykładzie 10a – slajd „Podwyższenie temperatury wrzenia (1)”.

9
Chem. Fiz. TCH II/12
9
Termodynamiczna
definicja aktywności (1)
Jeśli oba składniki roztworu są cieczami, to ich aktywność definiuje się:
A
A
A
a
RT
ln
0
+
=
µ
µ
B
B
B
a
RT
ln
0
+
=
µ
µ
RT
A
A
A
e
a
0
µ
µ −
=
RT
B
B
B
e
a
0
µ
µ −
=
Miarą aktywności jest mierzalna różnica potencjału chemicznego
składnika w roztworze i w stanie standardowym ( w tym przypadku
w stanie czystym).
W przypadku roztworów doskonałych aktywność
równa się ułamkowi molowemu.
Roztwory rzeczywiste o znacznych stężeniach nie stanowią ani roztworów
doskonałych, ani doskonale rozcieńczonych. Jak sobie zatem poradzić z opisem
termodynamicznym takich układów? Jedną z możliwości oferują wspomniane już
funkcje nadmiarowe. Aktywności (Lewis) stanowią drugą z nich – chyba
najczęściej wykorzystywaną.
10
Chem. Fiz. TCH II/12
10
Współczynniki aktywności
(1)
Współczynniki aktywności definiuje się:
A
A
A
x
a
=
γ
B
B
B
x
a
=
γ
(
)
A
A
A
A
RT
x
RT
γ
µ
µ
ln
ln
0
=
+
−
(
)
B
B
B
B
RT
x
RT
γ
µ
µ
ln
ln
0
=
+
−
B
RT
γ
ln
To różnica potencjału chemicznego składnika w
roztworze rzeczywistym i tego jaki by składnik ten
miał, gdyby roztwór był roztworem doskonałym
11
Chem. Fiz. TCH II/12
11
Termodynamiczna
definicja aktywności (2)
Jeśli jeden ze składników (B) jest wygodnie traktować jako substancję
rozpuszczoną , to jego aktywność definiuje się:
B
x
B
x
B
a
RT
ln
+
=
⊗
µ
µ
RT
B
x
B
x
B
e
a
⊗
−
=
µ
µ
B
m
B
m
B
a
RT
ln
+
=
⊗
µ
µ
B
c
B
c
B
a
RT
ln
+
=
⊗
µ
µ
RT
B
m
B
m
B
e
a
⊗
−
=
µ
µ
RT
B
c
B
c
B
e
a
⊗
−
=
µ
µ
Aktywność zaczyna zgadzać się ze stężeniem (w odpowiedniej skali)
gdy roztwór staje się doskonale rozcieńczony (zbliża się
termodynamicznie do niego), zatem wymagane są małe stężenia.
Jak widać są różne skale aktywności dla substancji rozpuszczonych.
Różnice między potencjałem chemicznym składnika w danym stanie (roztworze) a
w stanie standardowym są nadal mierzalne.
12
Chem. Fiz. TCH II/12
12
Współczynniki aktywności
(2)
Współczynniki aktywności (w odpowiedniej skali) substancji
rozpuszczonej definiuje się:
B
B
x
B
x
x
a
=
γ
B
B
m
B
m
m
a
=
γ
(
)
B
x
B
B
x
B
RT
x
RT
γ
µ
µ
ln
ln
=
+
−
⊗
B
RT
γ
ln
(w każdej skali) to różnica potencjału chemicznego
składnika w roztworze rzeczywistym i tego jaki by
składnik ten miał, gdyby roztwór był roztworem
doskonale rozcieńczonym
B
B
c
B
c
c
a
=
γ
(można też zapisać to dla
pozostałych skal)
13
Chem. Fiz. TCH II/12
13
Termodynamiczna
definicja aktywności (3)
Dla rozpuszczalnika:
1
→
→
A
A
A
x
a
γ
gdy
1
→
A
x
Dla substancji
rozpuszczonej:
1
)
,
(
→
→
B
B
B
B
B
c
m
x
a
γ
gdy
0
)
,
(
→
B
B
B
c
m
x
14
Chem. Fiz. TCH II/12
14
Wyznaczanie aktywności
(1)
Przyrównanie równań:
0
0
0
ln
ln
A
A
A
A
A
A
P
P
RT
f
f
RT
≅
=
−
µ
µ
A
A
A
a
RT
ln
0
=
−
µ
µ
pozwala zapisać:
0
0
A
A
A
A
A
P
P
f
f
a
=
=
a łącznie z równaniem Gibbsa-Duhema:
0
ln
ln
=
+
B
B
A
A
a
d
n
a
d
n
co pozwala na wyznaczanie aktywności w oparciu o pomiary
prężności cząstkowej w parze nasyconej nad roztworem
pozwala na wyznaczenie – omawianą już metodą graficzną – także
aktywności drugiego składnika.
Pomiary są prostsze, gdy substancja rozpuszczona jest nielotna.
15
Chem. Fiz. TCH II/12
15
Wyznaczanie aktywności
(2)
Także pomiary ebuliometryczne i kriometryczne umożliwiają
pomiar aktywności, można bowiem dowieść, że :
T
RT
H
P
P
a
p
A
A
A
∆
∆
−
=
=
2
0
ln
ln
co łącznie z równaniem Gibbsa-Duhema pozwala na wyznaczenie
aktywności obu składników.
T
RT
H
a
t
A
∆
∆
−
=
2
ln
Patrz slajd „Podwyższenie temperatury wrzenia (3)” – wykład 10A.
Częściej stosuje się kriometrię, ze względu na większe (dokładniej mierzalne)
wartości ∆T.

16
Chem. Fiz. TCH II/12
16
Zależność współczynników
aktywności od temperatury
Można dowieść, że – jeśli aktywności obu składników są
standaryzowane tak samo :
2
0
ln
RT
H
H
T
A
A
P
A
−
−
=
∂
∂
γ
gdzie licznik ułamka po prawej stronie, tzw. względna cząstkowa
molowa entalpia jest równa różniczkowemu ciepłu rozpuszczania.
Jeśli jednak substancja B jest standaryzowana na roztwór
nieskończenie rozcieńczony, to:
2
0
ln
RT
H
H
T
B
B
P
B
−
−
=
∂
∂
γ
2
0
ln
RT
H
H
T
B
B
P
B
−
−
=
∂
∂
γ
gdzie licznik ułamka jest pierwszym
ciepłem rozpuszczania B.
Wyszukiwarka
Podobne podstrony:
chf tch I wykl 010Ac
chf tch I wykl 004c
chf tch I wykl 010a
chf tch I wykl 007c
chf tch I wykl 001c
chf tch I wykl 001c
chf tch I wykl 005b
chf tch I wykl 004b
chf tch I wykl 006b
chf tch I wykl 008c
chf tch I wykl 009c
chf tch I wykl 003c
chf tch I wykl 002c
chf tch I wykl 005c
chf tch I wykl 010c
chf tch I wykl 006c
chf tch I wykl 011c
chf tch I wykl 010Ac
więcej podobnych podstron