
1
Chem. Fiz. TCH II/02
1
Kontakt,informacja i konsultacje
• tablica ogłoszeń Katedry Chemii Fizycznej
http://www.pg.gda.pl/chem/Dydaktyka/ lub
http://www.pg.gda.pl/chem/Katedry/Fizyczna
• Konsultacje: wtorki 16-17, czwartki 13-15
• Chemia „A”; pokój 307
• Telefon: 347-2769
• E-mail: wojtek@chem.pg.gda.pl

2
Chem. Fiz. TCH II/02
2
I Zasada Termodynamiki
H. Helmholtz (1847)
Jeżeli w układzie izolowanym znika
jeden rodzaj energii, to równocześnie
musi powstawać drugi w ilości ściśle
równoważnej.
Nie jest możliwe zbudowanie perpetuum mobile
pierwszego rodzaju.
Całkowita energia układu izolowanego jest stała.
Wynika z tego także, iż całkowita energia układu i jego otoczenia jest stała.

3
Chem. Fiz. TCH II/02
3
Układ zamknięty
Istnieje funkcja stanu, której różnica wartości przy
przejściu między dwoma stanami równa jest
energii wymienionej z otoczeniem podczas tego
przejścia .
Energia wewnętrzna
Całkowita energia układu
Symbol u lub U
U – molowa, u – całkowita.

4
Chem. Fiz. TCH II/02
4
Nazywamy nimi wielkości termodynamiczne jednozna-
cznie określone przez stan układu, tym samym nieza-
leżne od drogi, jaką stan ten został osiągnięty.
Energia wewnętrzna jest funkcją stanu!!!
∆u = q + w
lub
du = dq + dw
Funkcje stanu (1)

5
Chem. Fiz. TCH II/02
5
du = dq – PdV
u=f(P,T) u=f(V,T) u=f(V,P)
różniczki zupełne
Funkcje stanu (2)
∫
=
∆
k
p
V
V
P(V)dV
-
q
u
Matematyczną konsekwencją faktu, że jakaś wielkość jest funkcją stanu, jest to,
że wielkość ta jest różniczką zupełną parametrów stanu.

6
Chem. Fiz. TCH II/02
6
Różniczki zupełne energii wewnętrznej
Funkcje stanu (3)
dT
dT
du
dP
dP
du
du
P
T
+
=
dT
dT
du
dV
dV
du
du
V
T
+
=
dP
dP
du
dV
dV
du
du
V
P
+
=
NIE SĄ różniczkami zupełnymi dw i dq (bo w i q nie są funkcjami stanu).
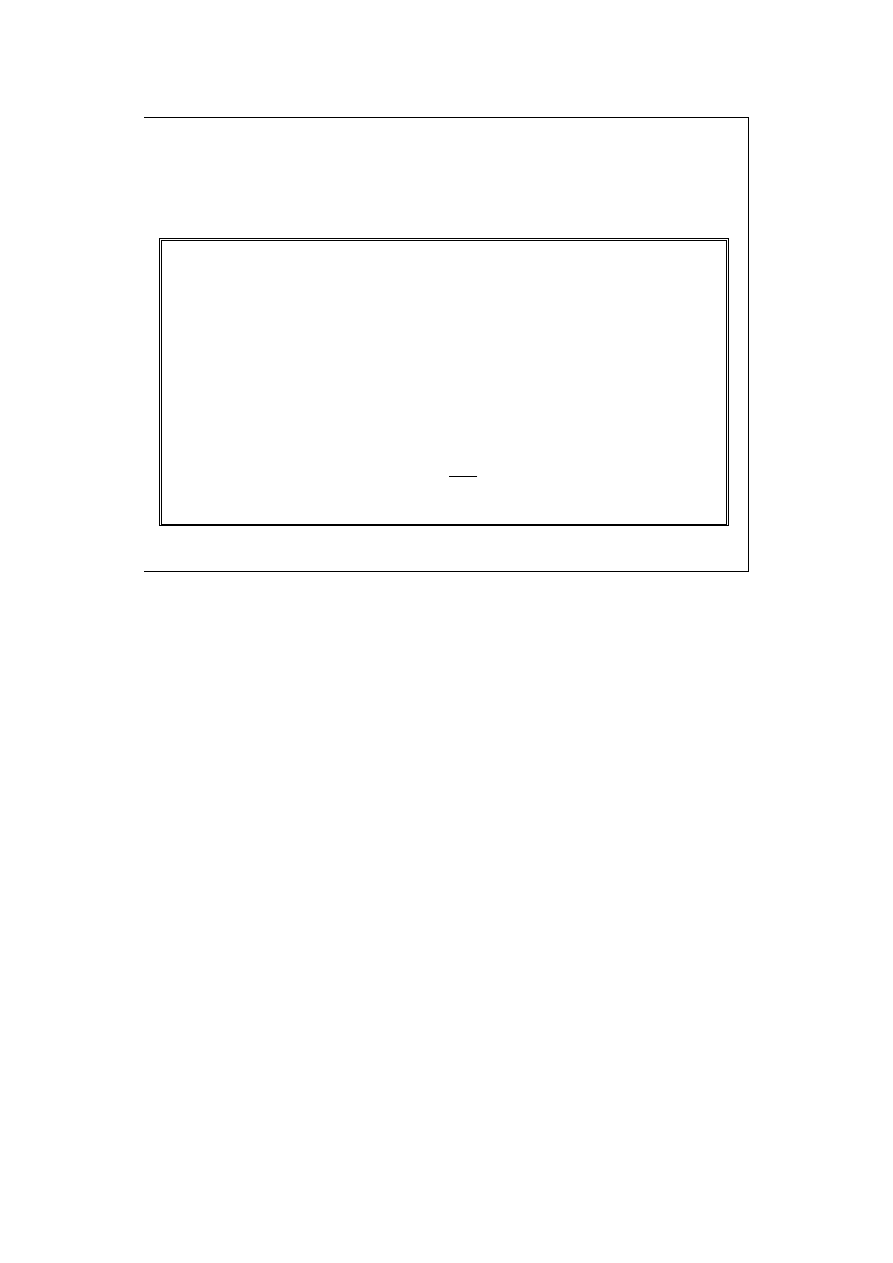
7
Chem. Fiz. TCH II/02
7
Izochora (V=const.)
∆u= u
2
-u
1
=q
V
Dla reakcji chemicznej: q
V
=Q
V
=
∆U
Bez reakcji: dq
V
=c
V
dT
Znamy więc pochodną cząstkową:
Energia wewnętrzna
przemian izochorycznych
V
V
dT
dU
C
=
Dla całego układu stosujemy oczywiście symbole małe c i małe u.
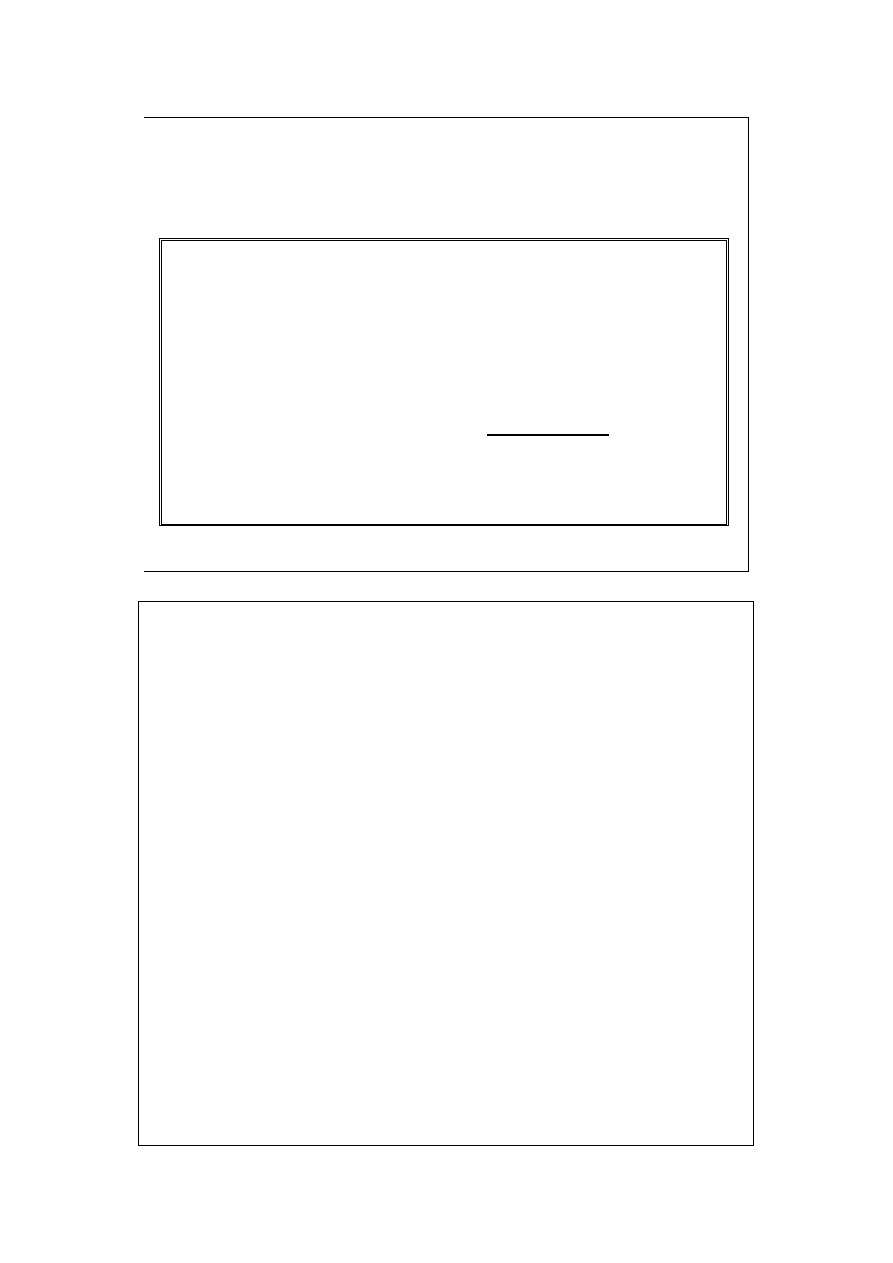
8
Chem. Fiz. TCH II/02
8
Molowa pojemność cieplna przy stałej objętości,
C
V
(dla celów obliczeniowych przyjmować będziemy niezależność C
V
od temperatury, co jest uproszczeniem)
Energia wewnętrzna
przemian izochorycznych
...
3
2
+
+
+
+
=
dT
cT
bT
a
C
V
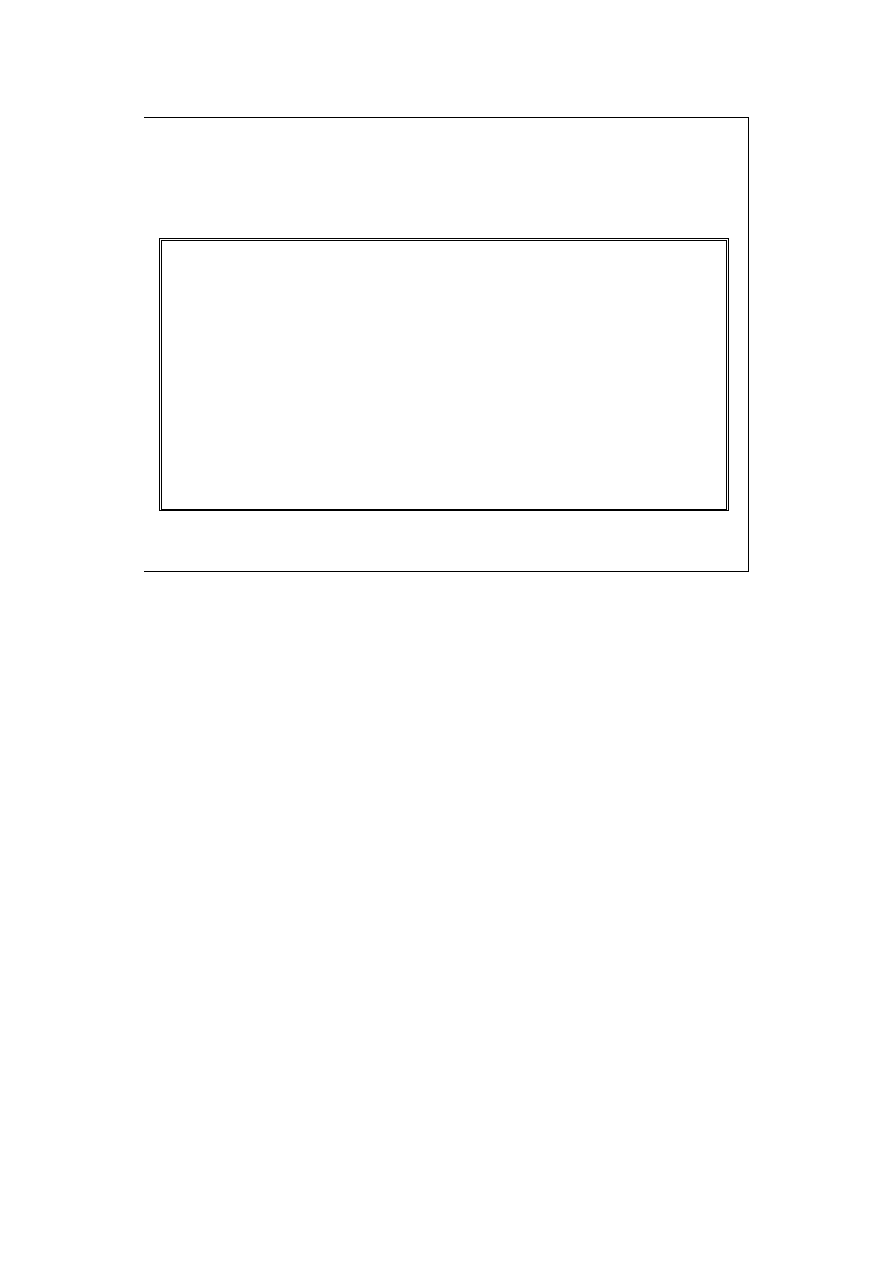
9
Chem. Fiz. TCH II/02
9
Izobara (P=const.)
dw=-PdV w=-P(V
k
-V
p
)=-P
∆V
wtedy:
∆u=q
P
-P
∆V
u
k
-u
p
=q
P
-P(V
k
-V
p
)
q
P
=(u
k
+PV
k
)-(u
p
+PV
p
)
h=u+PV
Energia wewnętrzna
przemian izobarycznych
h=u+PV jest funkcją stanu bo jest funkcją innej funkcji stanu i parametrów stanu

10
Chem. Fiz. TCH II/02
10
q
p
=
∆h = h
k
-h
p
lub Q
p
=
∆H = H
k
-H
p
Entalpia
P
P
dT
dH
C
=
P
T
V
P
dT
dV
dV
dU
P
C
C
+
=
−
gdzie (dU/dV)
T
jest ciśnieniem wewnętrznym
znów wielkości dla układu będą definiowane tak samo, lecz z zastosowaniem
małych liter jako symboli.
Ciśnienie wewnętrzne charakteryzuje oddziaływania międzycząsteczkowe
powodujące wzrost energii wewnętrznej układu zależnie od objętości.
Dla gazów rozrzedzonych, a ściślej – dla gazu doskonałego, ciśnienie
wewnętrzne jest równe zeru.
Wyprowadzenie wzoru na różnicę mogą sobie zainteresowani przestudiować z
podręcznika.

11
Chem. Fiz. TCH II/02
11
Dla gazu doskonałego:
C
p
-C
V
=P(dV/dT)
P
ponieważ V=RT/P, więc (dV/dT)
P
=R/P i C
p
-C
V
=R
Doświadczenie Joule’a
nie wymieniono ciepła
nie zmieniła się temperatura
gaz nie wykonał pracy (ekspansja do
próżni)
Molowe pojemności cieplne
Wniosek z dośw. Joule’a: energia wewnętrzna gazu nie zależy od jego objętości
w warunkach stałej temperatury.
C
P
rozwija się zatem w szereg podobny jak C
V
dla wyrażenia jego zależności od
temperatury, na ćwiczeniach często będziemy przyjmować jego niezależność od
T (uproszczenie!).

12
Chem. Fiz. TCH II/02
12
Doświadczenie Joule’a -
wnioski
0
=
du
dT
C
dV
dV
du
dT
dT
du
dV
dV
du
du
V
T
V
T
+
=
+
=
zatem:
dT
C
dV
dV
du
V
T
−
=
u
V
T
dV
dT
C
dV
du
−
=
ergo:
0
=
T
dV
du
QED
Przecież C
v
jesr różne od zera.

13
Chem. Fiz. TCH II/02
13
Adiabata odwracalna
0
=
q
PdV
dw
dU
−
=
=
równocześnie:
i ostatecznie:
dT
nC
dU
V
=
V
nRT
P
=
zatem:
dV
V
nRT
dT
nC
V
−
=
dV
V
R
T
dT
C
V
−
=
po scałkowaniu:
a ponieważ C
P
-C
V
=R:
k
p
p
k
V
V
V
R
T
T
C
ln
ln
=
1
ln
ln
)
1
(
ln
−
=
−
=
κ
κ
k
p
k
p
p
k
V
V
V
V
T
T
1
−
=
κ
k
p
p
k
V
V
T
T
i:
const
PV
V
P
V
P
p
p
k
k
=
=
=
κ
κ
κ
Ostatnie przekształcenie uzyskuje się używając równania gazu doskonałego.
Na razie przyjmujemy, że stosunek C
P
/C
V
=7/5 dla gazu dwuatomowego i 5/3 dla
jednoatomowego.
Wytłumaczenie tego faktu nastąpi później.

14
Chem. Fiz. TCH II/02
14
Układ P-V
Politropy
Politropa pV
x
=const. Jej rodzaj zależy od wartości wykładnika x.

15
Chem. Fiz. TCH II/02
15
Dla reakcji chemicznej prowadzonej w warunkach
izochorycznych:
Q
V
=(
∆U)
V
≈ (∆U)
P
Dla reakcji chemicznej prowadzonej w warunkach
izobarycznych:
Q
P
=(
∆H)
P
∆H=∆U+P∆V
Q
P
=Q
V
+P
∆νV
∆H=∆U+P∆νRT/P= ∆U+∆νRT
∆ν=n
reagentów gazowych poreakcji
- n
reagentów gazowych przed reakcją
Termochemia

16
Chem. Fiz. TCH II/02
16
Ponieważ entalpia jest funkcją stanu, a więc
zmiana entalpii (ciepło reakcji chemicznej)
nie zależy od drogi syntezy
(wieloetapowej) jeśli tylko wszystkie etapy
zachodzą izobarycznie.
To samo dotyczy energii wewnętrznej
w przypadku procesów izochorycznych
Termochemia -
prawo Hessa

17
Chem. Fiz. TCH II/02
17
Jeśli ustalimy, że reakcja docelowa, X, dla
której chcemy obliczyć ciepło reakcji, jest
kombinacją liniową kilku reakcji A, B, C, ...
Np. X= 2A-B+C
To ciepło reakcji jest analogiczną kombinacją
liniową ciepeł reakcji składowych (etapów
syntezy).
∆H
X
=2
∆H
A
-
∆H
B
+
∆H
C
Prawo Hessa –
algorytm (1)
∆H reakcji odwrotnej do A jest taka sama, lecz z przeciwnym znakiem.
Jeżeli musimy „wziąć” do kombinacji kilka jednakowych reakcji to jej ciepło mnożymy
tyleż razy (
∆H lub ∆U).

18
Chem. Fiz. TCH II/02
18
Prawo Hessa –
algorytm (2)
1. Wybór reakcji wyjściowej z jednym przynajmniej
reagentem po tej samej stronie, co w reakcji docelowej
2. Wprowadzanie kolejnych reagentów, potem
usuwanie nie występujących w reakcji docelowej
3. Jeżeli reakcja uzyskana po kolejnym dodaniu etapu
jest zgodna z reakcją docelową, to koniec, w przeciw-
nym razie – powrót do 2 etapu.
Reagent w kroku 1 powinien być możliwie charakterystyczny.
W kroku 2 nigdy nie używaj reakcji już użytej (skreśl ją z listy).

19
Chem. Fiz. TCH II/02
19
Ciepła tworzenia i spalania
(1)
Ciepło tworzenia związku jest to ciepło reakcji powstawania tego
związku w ilości 1 mola z pierwiastków będących w odmianach
trwałych termodynamicznie w danych warunkach.
Standardowe molowe ciepło tworzenia jest ciepłem tworzenia w
warunkach standardowych.
Standardowa entalpia tworzenia jest standardową entalpią danego
związku chemicznego.
Standardowe entalpie (tworzenia) pierwiastków (ich odmian
trwałych w warunkach standardowych) są równe ZERU!!!
Tzw. „synteza totalna”.

20
Chem. Fiz. TCH II/02
20
Ciepła tworzenia i spalania
(2)
0
298
,
,
,
1
0
298
,
,
,
1
0
298
,
s
tw
i
n
i
pr
tw
i
n
i
r
H
a
H
m
H
∆
−
∆
=
∆
∑
∑
=
=
0
298
,
,
,
1
0
298
,
,
,
1
0
298
,
pr
sp
i
n
i
s
sp
i
n
i
r
H
a
H
m
H
∆
−
∆
=
∆
∑
∑
=
=
Definicja ciepła spalania – analogiczna jak przy tworzeniu, ważna jest definicja
stanu produktów spalania, woda, azot, siarka.
m, a – współczynniki stechiometryczne w równaniu reakcji, odpowiednio po
stronie produktów i substratów
Pierwszy wzór ma znaczenie zasadnicze, wypływa bezpośrednio z faktu, że
entalpia jest funkcją stanu
Wyszukiwarka
Podobne podstrony:
chf tch I wykl 010Ac
chf tch I wykl 004c
chf tch I wykl 010a
chf tch I wykl 007c
chf tch I wykl 001c
chf tch I wykl 012c
chf tch I wykl 001c
chf tch I wykl 005b
chf tch I wykl 004b
chf tch I wykl 006b
chf tch I wykl 008c
chf tch I wykl 009c
chf tch I wykl 003c
chf tch I wykl 005c
chf tch I wykl 010c
chf tch I wykl 006c
chf tch I wykl 011c
chf tch I wykl 010Ac
więcej podobnych podstron