1

Chem. Fiz. TCH II/04

1

Entropia - obliczanie.

Podsumowanie

∫

=

−

=

∆

2

1

)

(

1

2

T

T

V

dT

T

T

C

S

S

S

∫

=

−

=

∆

2

1

)

(

1

2

T

T

P

dT

T

T

C

S

S

S

p

k

S

S

S

−

=

∆

1

2

1

2

ln

ln

V

V

R

T

T

C

S

V

+

=

∆

1

2

1

2

ln

ln

P

P

R

T

T

C

S

P

−

=

∆

w izobarze:

Funkcja stanu !

w izochorze:

dla gazu doskonałego:

2

Chem. Fiz. TCH II/04

2

Entropia, jako miara

uporządkowania (1)

GAZ

W gazie ruch cząstek jest chaotyczny (przypadkowy) i najszybszy ze wszystkich

stanów skupienia.
W modelu gazu doskonałego pomija się nawet wszelkie oddziaływania atomów
czy molekuł gazu między sobą (zakłada się jedynie sprężyste odbicia).

3

Chem. Fiz. TCH II/04

3

Entropia, jako miara

uporządkowania (2)

CIECZ

W cieczach, choć pod wieloma względami nie różnią się od gazów (stąd
płyny!!!), obserwujemy:
•znacznie powolniejsze ruchy termiczne,
-znacznie większą gęstość: do 1000 razy (choć można sprężyć gaz do podobnej
gęstości, bez przemiany fazowej – skraplania - byle powyżej temperatury
krytycznej),
-pewien stopień uporządkowania (mniej lub bardziej uporządkowane struktury
(agregaty),
-oddziaływania międzycząsteczkowe (znacznie silniejsze niż w gazach
rzeczywistych) aż do wiązań chemicznych (kowalencyjnych - wodorowe).

4

Chem. Fiz. TCH II/04

4

Entropia, jako miara

uporządkowania (3)

CIAŁO STAŁE

Kryształ – nieruchome atomy w węzłach sieci.
Mogą jednak drgać (oscylować), a przy ogólnie niskich energiach
(temperaturach) - wchodzi w rachubę także ruch elektronów (zwłaszcza w
metalach).

5

Chem. Fiz. TCH II/04

5

Entropia, jako miara

uporządkowania (4)

CIAŁO STAŁE

GAZ
CIECZ

uporządkowanie

entropia

Ludwig Eduard

Boltzmann

W

k

S

ln

=

Wszelkie przemiany prowadzące do wzrostu nieuporządkowania wykazują

dodatnią zmianę entropii (układu).

Na przykład ROZPUSZCZANIE, zwłaszcza substancji krystalicznych. !!!!

Jeśli w reakcji chemicznej dochodzi do przyrostu liczby moli substancji w stanie
gazowym, to na pewno towarzysząca jej zmiana entropii jest dodatnia.

6

Chem. Fiz. TCH II/04

6

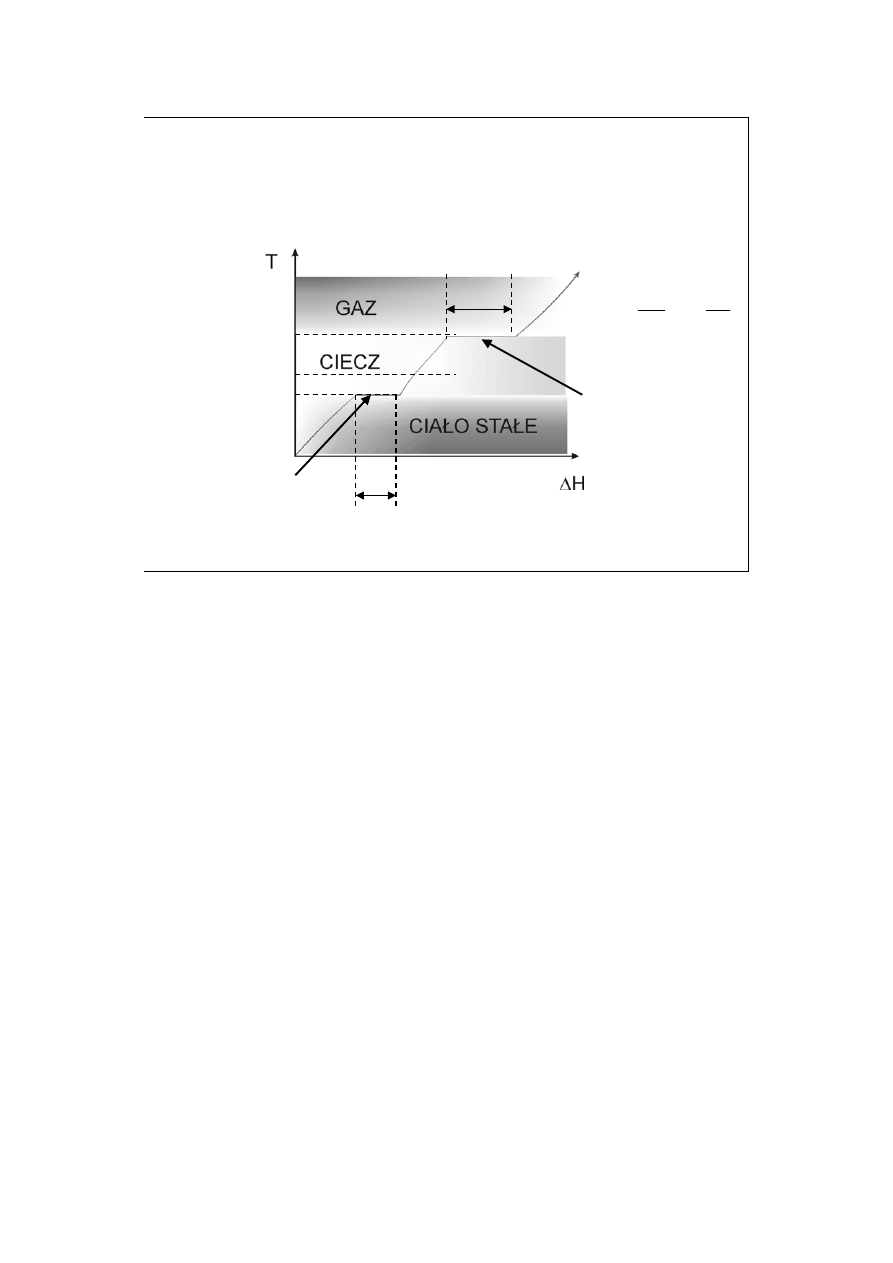
Krzywa ogrzewania (1).

T=298K; H

0

PF1 (topnienie)

PF2 (wrzenie)

P=const=1,013·10

5

Pa

∆H

2

∆H

1

T

PF2

=T

wrz

T

PF1

=T

top

P

P

C

H

T

tg

1

=













∂

∂

=

α

Temperatury przemian fazowych są NORMALNYMI temperaturami topnienia i

wrzenia, bowiem ciśnienie jest standardowe.
Gdyby C

P

nie zależało od temperatury, linie ogrzewania poza przejściami

fazowymi byłyby liniami prostymi.

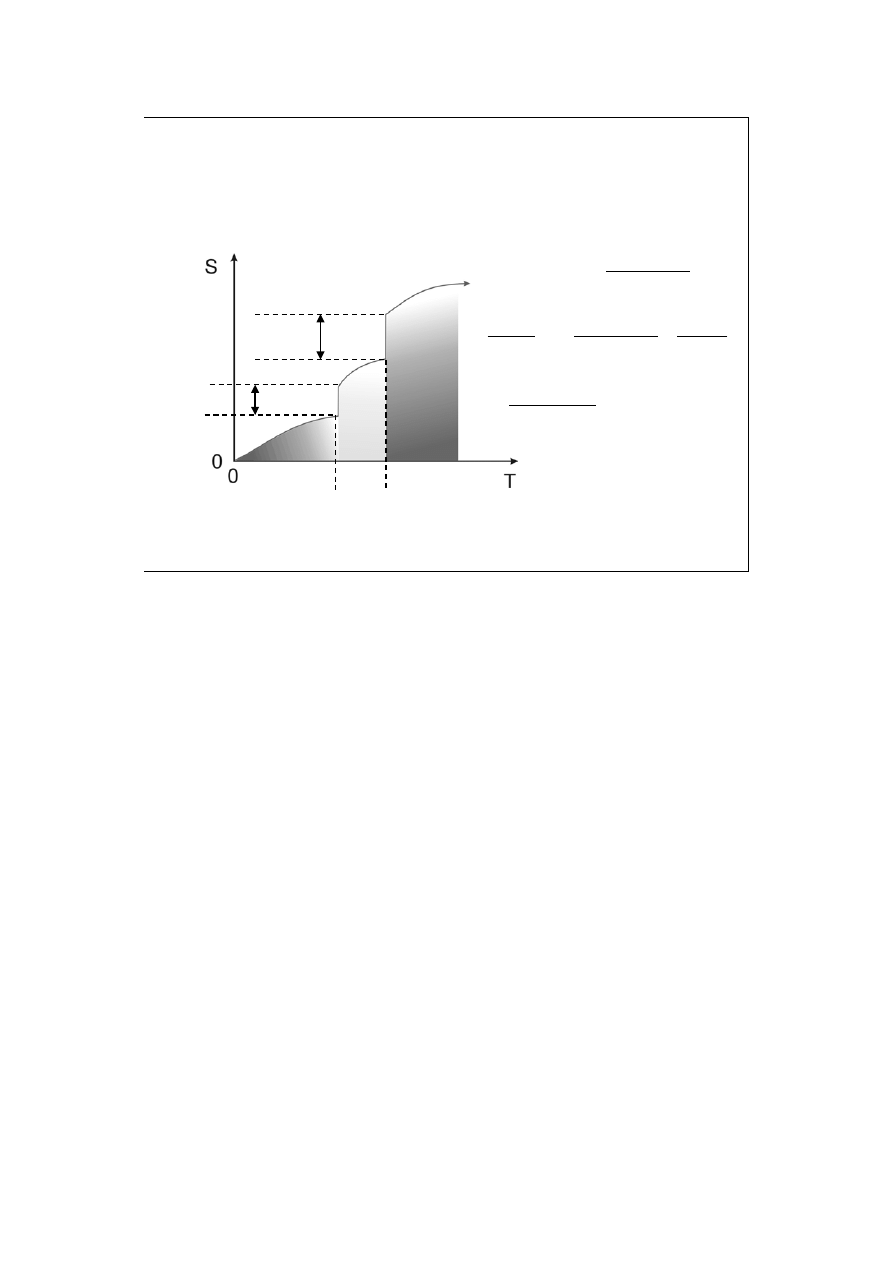
7

Chem. Fiz. TCH II/04

7

Krzywa ogrzewania (2).

Entropia absolutna

T

top

T

wrz

∆S

wrz

∆S

top

S(0)

∫

∫

∫

+

∆

+

+

∆

+

+

=

T

T

g

P

wrz

par

T

T

c

P

top

top

T

s

P

wrz

wrz

top

top

T

dT

T

C

T

H

T

dT

T

C

T

H

T

dT

T

C

S

T

S

)

(

)

(

)

(

)

0

(

)

(

,

,

0

,

W podanej całce nie da się obliczyć ln(0), stąd dla najniższych temperatur CP

nie ma członu stałego, tylko wyższe potęgi (np. tzw. „ekstrapolacja Debye’a).

8

Chem. Fiz. TCH II/04

8

III Zasada Termodynamiki

(1)

Teoremat cieplny Nernsta:

Gdy temperatura zmierza do zera

bezwzględnego, zmiana entropii

towarzysząca dowolnym przemianom

fizycznym lub chemicznym dąży do zera:

∆S →0, gdy T→0

Ekstrapolacja Debye’a:

3

aT

C

P

=

0

lim

0

=

∆

→

T

S

Walther

Hermann Nernst

9

Chem. Fiz. TCH II/04

9

III Zasada Termodynamiki

(2)

Jeśli entropię każdego pierwiastka w jego najbardziej trwałej postaci

przyjmiemy za równą zeru w T=0, to każda substancja ma entropię

dodatnią, która dla T=0 może przyjmować wartość zero, a która

przyjmuje taką wartość dla wszystkich doskonale krystalicznych

substancji (także związków chemicznych).

Dla substancji doskonałych

S(0)=0

Tzw ciecze nadciekłe, obserwowane w pobliżu zera bezwzględnego także
wykazują wysokie uporządkowanie (choć w ruchu, a nie statyczne).
Entropia resztkowa, , gdy są możliwe różne ustawienia równocennych
energetycznie stanów, elektrony (zaczyna rządzić mechanika kwantowa).

10

Chem. Fiz. TCH II/04

10

III Zasada Termodynamiki

(3)

Temperatura zera bezwzględnego jest nieosiągalna w skończonej

liczbie kroków obecny rekord to 20 nK.

3 nagrody Nobla za kriotechnikę (z fizyki):

• Onnes Heike Kamerlingh - 1913

• William Francis Giauque - 1949

• David M. Lee, Robert C. Richardson, Douglas D. Oshe-

roff - 1996

nR

PV

=

θ

1

=

−

=

g

z

g

θ

θ

θ

η

θ zdefiniowana z równania gazu doskonałego (musi osiągać zero, bowiem P i V
nie mogą być ujemne).
θ zdefiniowana w skali termodynamicznej z teorematu Carnota: sprawność
odwracalnej maszyny cieplnej wynosi 1, gdy temperatura zbiornika zimnego
wynosi 0 (a sprawność wyższa od 1 oznacza perpetuum mobile).
Dla uzyskania zgodności wielkości jednostki przyrostu temperatury ze stopniem
Celsjusza, przyjęto, że punkt potrójny wody ma w skali termodynamicznej
(bezwzględnej) temperaturę 273,16 K.

Nobliści (pamietajmy o polskim wkładzie w kriotechnikę: Wróblewski i
Olszewski)
Onnes – Holender - pierwszy skroplił hel, zaobserwował nadprzewodnictwo. W
jego laboratorium (jego uczeń Keesom) zestalono też hel w 1926 roku.
Giauque – Kanadyjczyk - w 1926 roku zaproponował metodę uzyskiwania
niskich temperatur (rozmagnesowanie adiabatyczne, niezależnie proponował ją
także Debye) – tzn. znacznie poniżej -272.15

o

C, lecz to on pierwszy zastosował

ją praktycznie w 1935, razem z D.P. MacDougallem.
Trójka Amerykanów – osiągnęła w/w rekord (zauważając nadciekłość

3

He.

11

Chem. Fiz. TCH II/04

11

Entropia standardowa (1)

Entropia przemiany fazowej (w temperaturze przemiany

fazowej), pod stałym ciśnieniem standardowym.

PF

PF

PF

T

H

S

∆

=

∆

Dla pierwiastków i związków chemicznych jest obliczana

zgodnie z podanymi wzorami (uwzględniającymi przemiany

fazowe) w temperaturze 298 K, pod ciśnieniem standardowym.

Jej wartości (na jeden mol) znajdujemy w tablicach.

S

0

298

Molowa standardowa entropia (absolutna) pierwiastków (w odróznieniu od
stadardowej molowej entalpii - tworzenia) NIE jest równa zeru !!!

Dla wodnych roztworów elektrolitów przyjmuje się standardową molową
entropię jonu wodorowego za równą zeru w każdej temperaturze. Konwencja ta
potrzebna jest do rozdzielenia mierzalnej entropii soli w roztworze na udziały
kationu i anionu.

12

Chem. Fiz. TCH II/04

12

Entropia standardowa (2)

Dla reakcji chemicznych pod stałym ciśnieniem, standardowa

molowa entropia obliczana jest wg wzoru:

Entropia jest ekstensywną funkcją stanu.

Jednostki: J·K

-1

, lub (dla molowej) J·K

-1

·mol

-1

0

298

,

,

1

0

298

,

,

1

0

298

,

s

i

n

i

pr

i

n

i

r

S

a

S

m

S

∑

∑

=

=

−

=

∆

13

Chem. Fiz. TCH II/04

13

Reguła Troutona

Standardowa molowa entropia parowania w przybliżeniu

wynosi

85 J·K

-1

·mol

-1

Gdy dowolna ciecz paruje, powstaje w przybliżeniu taka sama

„ilość nieporządku”.

Odstępstwa od tej reguły obserwuje się, gdy w cieczy istnieją

oddziaływania specyficzne, np. woda (109,1 J·K

-1

·mol

-1

), w

której istnieją wiązania wodorowe.

Praktycznie możemy więc oszacować ciepła parowania znając temperatury
wrzenia cieczy (i stosując regułę Troutona).
Wyjątkami są także bardzo lekkie gazy (ze względu na słabe wzbudzenie
rotacyjne).

14

Chem. Fiz. TCH II/04

14

Czy reakcja chemiczna jest

samorzutna? (1)

0

.

.

>

∆

+

∆

=

∆

ot

ukł

i

u

S

S

S

Dana jest reakcja: S(s,romb) + O

2

(g) = SO

2

(g)

Czy może ona zachodzić samorzutnie w warunkach standardowych?

248,22

-296,83

SO

2

(g)

205,14

0

O

2

(g)

31,80

0

S(s,romb.)

S

0

298

J/(K·mol)

∆H

0

tw298

kJ/mol

J/K

28

,

11

)

14

,

205

80

,

31

(

)

22

,

248

(

0

298

,

=

+

−

=

∆

=

∆

r

ukł

S

S

J

296830

0

298

,

−

=

∆

r

H

J/K

996

298

296830 ≅

=

∆

−

=

∆

T

H

S

ukł

ot

0

J/K

1007

996

28

,

11

.

.

>

≅

+

=

∆

i

u

S

JEST!!!

15

Chem. Fiz. TCH II/04

15

Entalpia swobodna (1)

Josiah Willard

Gibbs

ot

ukł

i

u

S

S

S

∆

+

∆

=

∆

.

.

T

H

S

S

r

r

i

u

∆

−

∆

=

∆

.

.

r

r

i

u

H

S

T

S

T

∆

−

∆

=

∆

.

.

r

r

i

u

S

T

H

S

T

∆

−

∆

=

∆

−

.

.

samorzutna

jest

reakcja

to

-

0

:

gdy

.

.

<

∆

−

i

u

S

T

TS

H

G

−

=

S

T

H

G

∆

−

∆

=

∆

Gibbs był Amerykaninem, w przyszłym roku (2003) mija 100 rocznica jego

śmierci.
Tę funkcję stanu nazywa się też czasem energią swobodną Gibbsa (ang. Gibbs
free energy).
Entalpia swobodna jest częścią entalpii, która może być użytecznie wykorzystana
z procesu (reakcji). Pozostała część zużywa się na wzrost nieuporządkowania.
We wzorze definicyjnym wszystkie symbole odnoszą się do reakcji (używa się
określeń człon entalpowy i człon entropowy). Człon entropowy określa nam
energię zmagazynowaną w układzie na sposób chaotyczny (nie uporządkowany).
Wskazuje nam, jaką energię możemy uzyskać z reakcji (sama egzotermiczność
nie wystarcza), jaką pracę (nie objętościową) można uzyskać z reakcji. To
ostatnie twierdzenie jest jeszcze wyraźniejsze w odniesieniu do energii
swobodnej, patrz slajd 21, gdzie praca objętościowa w ogóle nie występuje.

16

Chem. Fiz. TCH II/04

16

Entalpia swobodna (2)

∆S

r

<0

∆S

r

<0

nigdy nie jest

samorzutna

samorzutna, gdy

|

∆H

r

| <|T

∆S

r

|

∆S

r

>0

∆H

r

>0

endotermiczna

samorzutna, gdy

|

∆H

r

| >|T

∆S

r

|

zawsze samorzutna

∆S

r

>0

∆H

r

<0

egzotermiczna

Kryteria samorzutności reakcji:

Zawsze musi być: samorzutna, gdy

∆G

T,P

< 0

Warunek ogólny jest słuszny, gdy w procesie wykonywana jest tylko praca

objętościowa. (Warunek ogólniejszy zostanie omówiony na następnym
wykładzie).

17

Chem. Fiz. TCH II/04

17

Entalpia swobodna (3)

Entalpia swobodna jest funkcją stanu, zatem:

zawsze prawdziwe jest

∆G = G

k

- G

p

Jeżeli proces nie jest samorzutny, to znaczy, że samorzutny

jest proces odwrotny (zachodzący w kierunku przeciwnym).

Proces nie samorzutny może zostać ewentualnie

wymuszony.

18

Chem. Fiz. TCH II/04

18

Entalpia swobodna (4)

Dla reakcji chemicznej:

0

298

,

,

,

1

0

298

,

,

,

1

0

298

,

s

tw

i

n

i

pr

tw

i

n

i

r

G

a

G

m

G

∆

−

∆

=

∆

∑

∑

=

=

Dla pierwiastków chemicznych w ich trwałej

postaci, standardowa molowa entalpia swobodna

∆G

0

298

= 0

Dla związków mówimy o

∆G

tw

, którą

definiujemy analogicznie jak

∆H

tw

.

Dane są także stablicowane.

Dla protonu w roztworze wodnym, przyjmujemy konwencjonalnie

∆G

0

tw

=0 w

każdej temperaturze.

Związki egzo- i endoergiczne (możliwość syntezy totalnej, dla pierwszych
MOŻLIWA, dla drugich – NIE).

19

Chem. Fiz. TCH II/04

19

Energia swobodna

Hermann Ludwig

Ferdinand von Helmholtz

Dla warunków izochorycznych zdefiniowano
inną funkcję stanu, zwaną energią swobodną:

TS

U

F

−

=

S

T

U

F

∆

−

∆

=

∆

Kryterium samorzutności procesów (reakcji chemicznych)

zachodzących w warunkach izochorycznych jest:

∆F

V,T

< 0

Funkcja ta zwana jest także energią swobodną Helmholtza (ang. Helmholtz free

energy). Często nazywana jest także funkcją pracy maksymalnej lub funkcją
pracy i oznaczana także symbolem A (niem. Arbeit), wskazuje bowiem jaką
maksymalną pracę (tutaj na pewno nie objętościową) można uzyskać z układu.
Dowód na następnym wykładzie. Jej obliczenia dla przemiany fazowej, reakcji,
itp. są analogiczne jak sposoby określone dla entalpii swobodnej.
Jednostki są takie same jak dla energii wewnętrznej, entalpii i entalpii swobodnej
(J lub J/mol).
Także wszystkie konsekwencje wynikające z faktu, że jest ona funkcją stanu są
analogiczne.

20

Chem. Fiz. TCH II/04

20

Czy reakcja chemiczna jest

samorzutna? (2)

Dana jest reakcja: S(s,romb) + O

2

(g) = SO

2

(g)

Czy może ona zachodzić samorzutnie w warunkach standardowych?

-300,19

SO

2

(g)

0

O

2

(g)

0

S(s,romb.)

∆G

0

tw298

kJ/mol

kJ

19

,

300

0

298

,

0

298

,

2

−

=

∆

=

∆

twSO

r

G

G

JEST!!!

r

r

i

u

r

S

T

H

S

T

G

∆

−

∆

=

∆

−

=

∆

.

.

Sprawdzamy obliczenia z części (1).

Lewa strona:

Prawa strona:

kJ

19

,

300

1000

/

)

35

,

1007

298

(

.

.

−

=

⋅

−

=

∆

−

i

u

S

T

kJ

19

,

300

1000

/

)

28

,

11

298

(

83

,

296

−

=

⋅

−

−

=

∆

−

∆

r

r

S

T

H

21

Chem. Fiz. TCH II/04

21

Czy reakcja chemiczna jest

samorzutna? (3)

Dana jest reakcja: NaHCO

3

(s) = NaOH(s) + CO

2

(g)

Czy może ona zachodzić samorzutnie w warunkach standardowych?

-394,38

CO

2

(g)

-379,07

NaOH(s)

-851,9

NaHCO

3

(s)

∆G

0

tw298

kJ/mol

(

)

kJ

45

,

78

9

,

851

45

,

773

0

298

,

0

298

,

0

298

,

0

298

,

3

2

=

+

−

=

∆

−

−

∆

+

∆

=

∆

twNaCO

twNaOH

twCO

r

G

G

G

G

NIE JEST!!!

WNIOSEK:
• Wodorowęglan sodu jest termodynamicznie trwały w warunkach

standardowych.

22

Chem. Fiz. TCH II/04

22

Entalpia swobodna (5)

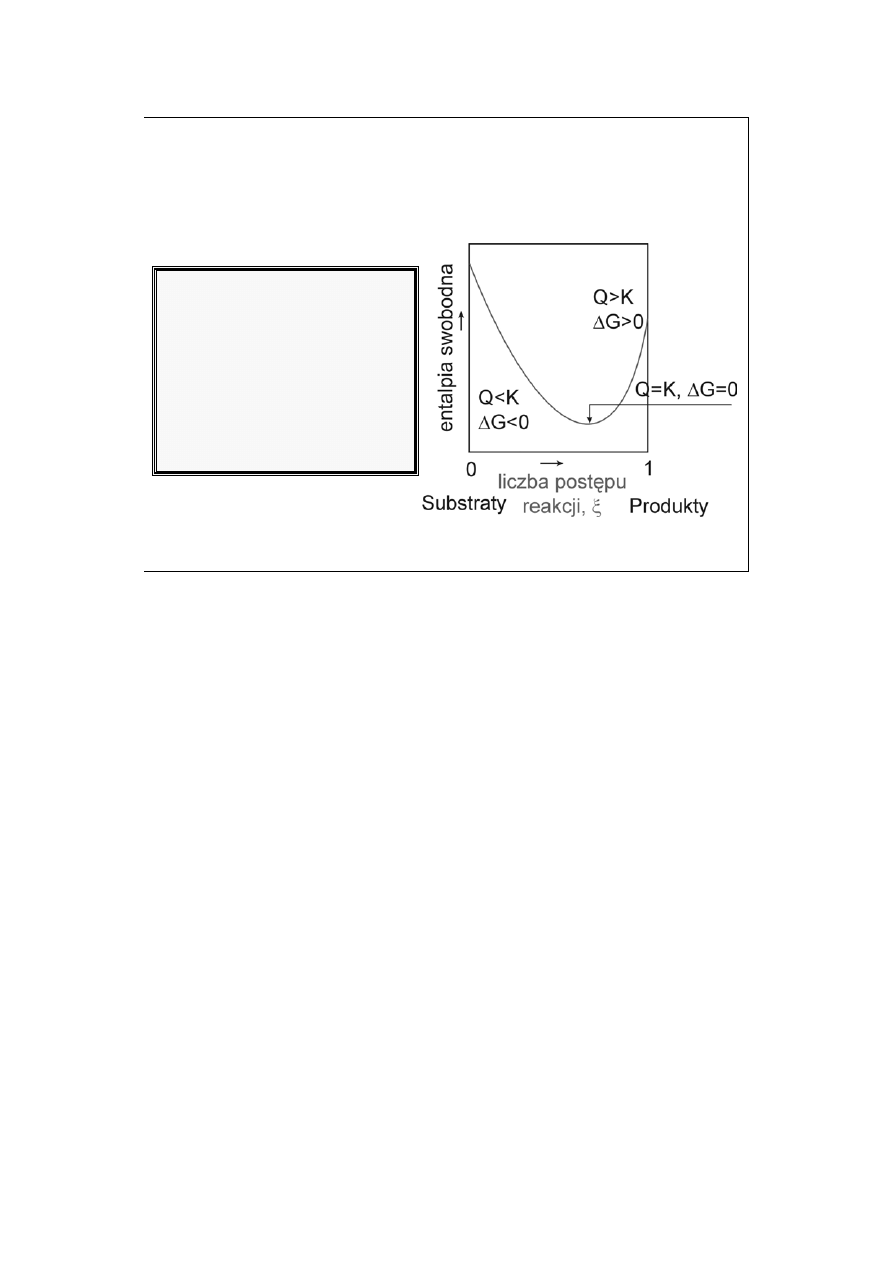
Zależnie od składu mieszani-
ny reakcyjnej możemy ocze-
kiwać samorzutnego przebie-
gu reakcji w prawo, w lewo
(samorzutnie przebiega reak-
cja przeciwna) lub pozosta-
wania przez nią w równowa-
dze.

23

Chem. Fiz. TCH II/04

23

Iloraz reakcji

...

...

⋅

⋅

⋅

⋅

=

n

N

m

M

b

B

a
A

a

a

b

a

Q

...

...

⋅

⋅

⋅

⋅

=

n

N

m

M

b

B

a
A

c

c

c

c

Q

Dla reakcji: aA + bB + ... = mM + nN + ...

gdzie aktywności (stężenia) są dowolne – odpowiadają konkretne-
mu, dowolnie wybranemu stanowi mieszaniny reakcyjnej (mogą
być nietrwałe w czasie). Gdy skład mieszaniny nie ulega zmianie
(reakcja pozostaje w równowadze), to Q = K (stała równowagi
reakcji), zaś aktywności lub stężenia odpowiadają tzw. składowi
równowagowemu mieszaniny reakcyjnej.

Aktywności zdefiniujemy sobie we właściwy czasie. Na razie używajmy stężeń

molowych (podzielonych przez stężenie jednostkowe, aby uniknąć wymiarów, Q
bowiem zawsze jest w ten sposób bezwymiarowe, niezależnie od wykładników a,
b, c, d).

Bliżej o związkach

∆G ze stałą równowagi reakcji i z ilorazem reakcji będziemy

mówić na wykładach z równowagi chemicznej.