1
Chem. Fiz. TCH II/03
1
Ciepła tworzenia i spalania
(3)
ponieważ:
Standardowa entalpia tworzenia jest standardową entalpią związku
Dla pierwiastków:
Dla związków:
0
298
,
0
298
tw
H
H
∆
=
∫
=
∆
T
p
T
tw
dT
T
C
H
298
0
,
)
(
∫
+
∆
=
∆
T
p
tw
T
tw
dT
T
C
H
H
298
0
298
,
0
,
)
(
P
P
C
T
H
=
∂
∂
Odnośnie pierwiastków – wzór dotyczy odmian trwałych termodynamicznie w
zakresie temperatur od 298K do T !!!
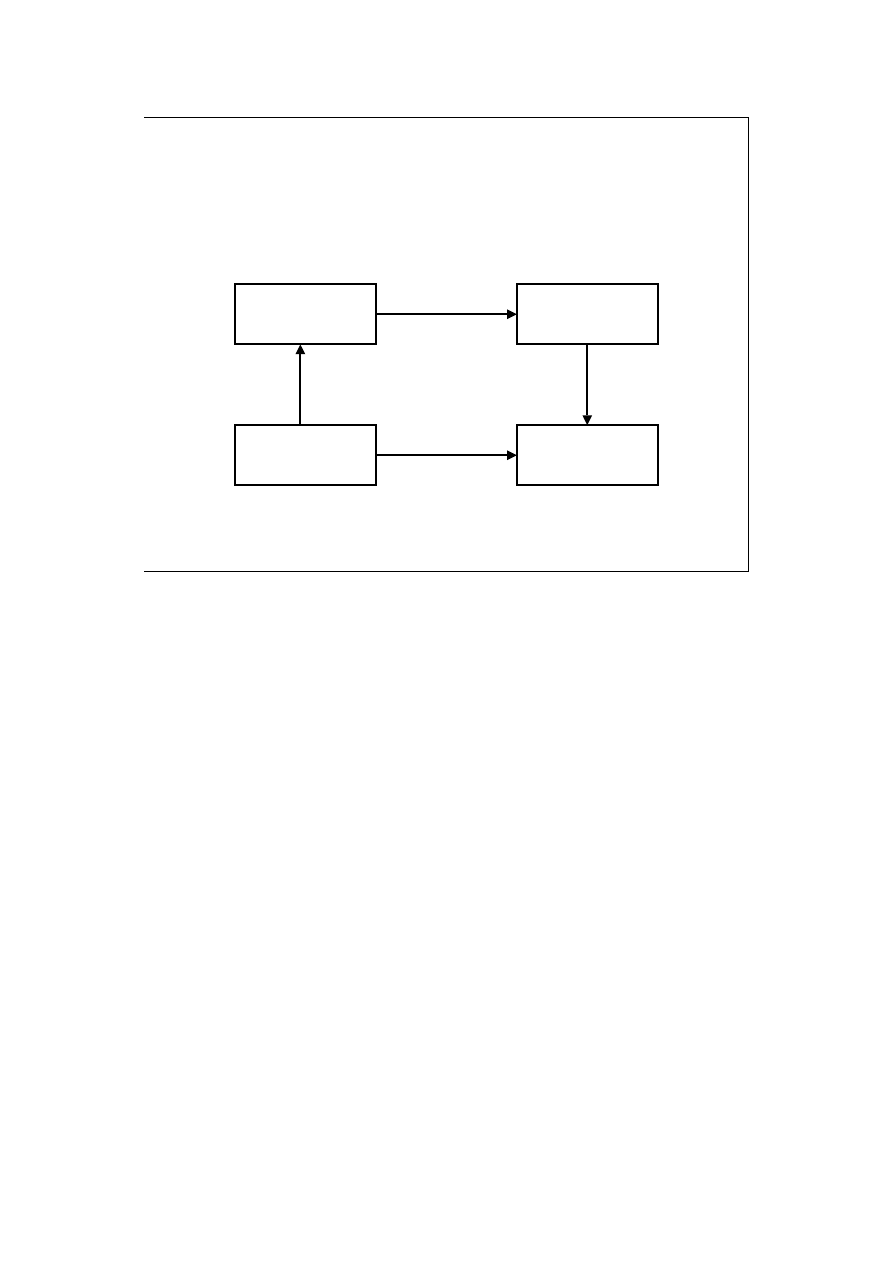
2
Chem. Fiz. TCH II/03
2
Prawo Kirchoffa (1)
Jak wyliczyć ciepło reakcji w innej temperaturze?
T
1
T
2
∆H
r,T1
∆H
r,T2
Produkty w T
1
Substraty w T
1
Produkty w T
2
Substraty w T
2
∆H
ogrz. substr.
∆H
chł. prod.
T
2
> T
1
Proszę zwrócić uwagę na przedstawiony cykl! Podobne podejście będzie
stosowane bardzo często w rozwiązywaniu wielu problemów.
Zakładamy, że T
2
>T
1
, choć może być i odwrotnie.
3
Chem. Fiz. TCH II/03
3
Prawo Kirchoffa (2)
Entalpia jest funkcją stanu, zatem:
.
.
2
.
.
1
prod
chł
substr
ogrz
H
H
H
H
∆
+
∆
+
∆
=
∆
.
.
.
.
1
2
prod
chł
substr
ogrz
H
H
H
H
∆
−
∆
−
∆
=
∆
∫
∫
∫
∫
−
+
∆
=
−
−
∆
=
∆
2
1
2
1
1
2
2
1
.
,
.
,
1
.
,
.
,
1
2
T
T
substr
P
T
T
prod
P
T
T
prod
P
T
T
substr
P
dT
C
dT
C
H
dT
C
dT
C
H
H
dT
C
H
H
T
T
P
∫
∆
+
∆
=
∆
2
1
1
2
Dla reakcji:
aA + bB + ... = lL + mM + ...
(
)
P
r
PB
PA
PM
PL
r
P
T
H
bC
aC
mC
lC
C
∂
∆
∂
=
−
−
−
+
+
=
∆
...
...
,
Całkiem analogiczne wzory obowiązują dla ciepeł reakcji (
∆U
r
) prowadzonych w
warunkach izochorycznych !!!
4
Chem. Fiz. TCH II/03
4
II Zasada Termodynamiki
(1)
Zasada ta pozwala nam określić jakie procesy zachodzą samorzutnie.
Nie jest możliwe zbudowanie maszyny pracującej
okresowo, która przeprowadzałaby ciepło w
równoważną ilość pracy bez powodowania zmian
w układzie lub otoczeniu.
Nie jest możliwe zbudowanie perpetuum mobile
drugiego rodzaju.
Np. I zasada dopuszczałaby przepływ ciepła od ciała chłodniejszego do
cieplejszego bez zmian w układzie lub jego otoczeniu (byleby była zachowana
zasada zachowania energii), lub przepływ gazu z naczynia o niższym ciśnieniu do
naczynia o wyższym ciśnieniu.
5
Chem. Fiz. TCH II/03
5
II Zasada Termodynamiki
(2)
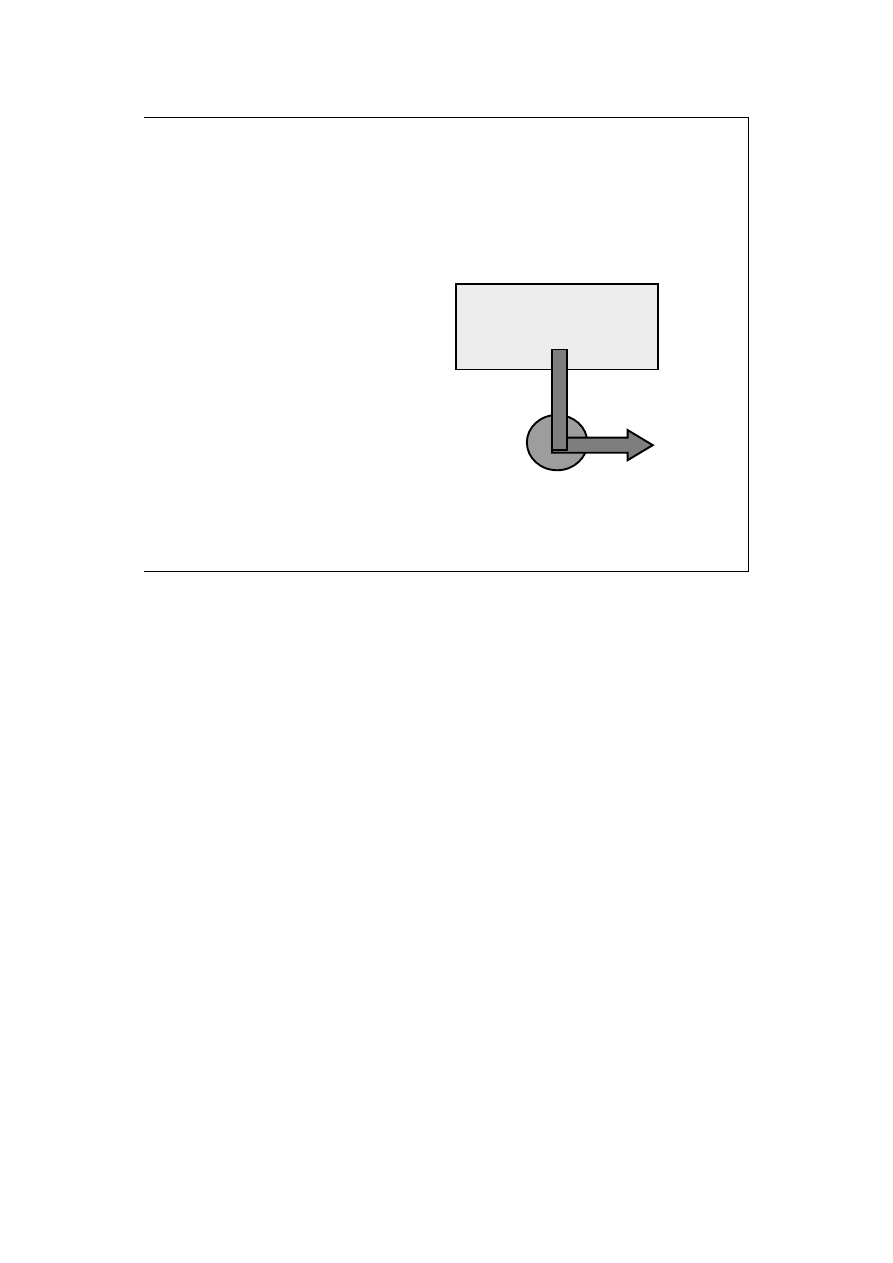
Sformułowanie lorda Kelvina (Williama Thomsona) :
Nie jest możliwy proces,
którego jedynym skutkiem
byłoby pobieranie ciepła ze
zbiornika i całkowita za-
miana tego ciepła w pracę.
zbiornik ciepła
CIEPŁO
PRACA
6
Chem. Fiz. TCH II/03
6
II Zasada Termodynamiki
(3)
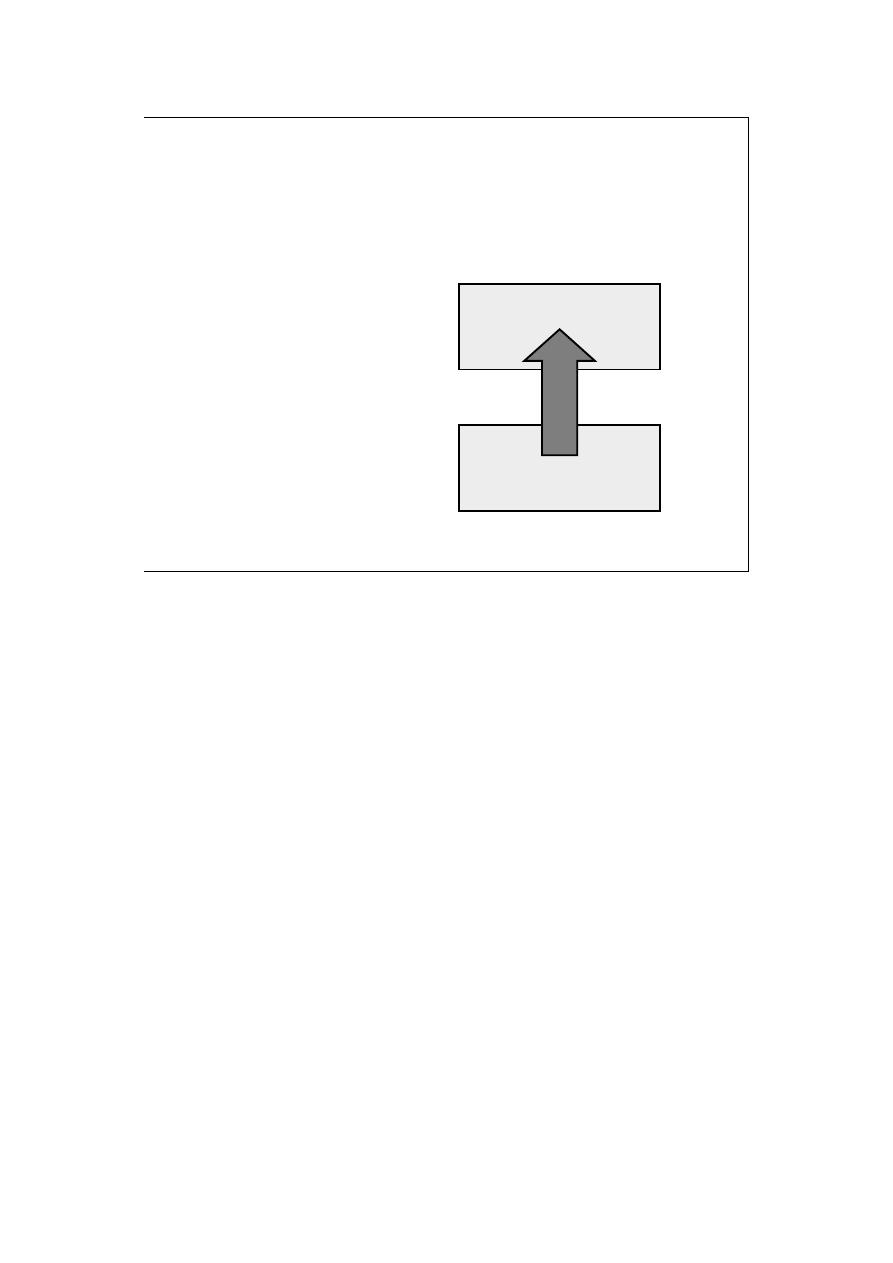
Sformułowanie Clausiusa :
Nie jest możliwy proces,
którego jedynym skutkiem
byłoby przeniesienie ener-
gii na sposób ciepła z ciała
chłodniejszego do cieplej-
szego.
wysoka temperatura
CIEPŁO
niska temperatura
Ciepło jest wyjątkową postacią energii pod względem jego zamiany na pracę.
Wszystkie inne rodzaje energii mogą bowiem bez ograniczeń ulegać zamianie
jedna w drugą, oraz na ciepło.
7
Chem. Fiz. TCH II/03
7
II Zasada Termodynamiki
(4)
Teoremat Carnota:
Wszystkie odwracalne maszyny cieplne
pracujące między dwiema temperaturami
mają tę samą sprawność, która jest wyższa
od sprawności każdej nieodwracalnej
maszyny cieplnej pracującej między tymi
temperaturami.
Sadi Carnot
2
2
1
2
q
q
q
q
w
+
=
−
=
η
1
2
T
T
>
w
q
q
u
−
=
+
=
∆
2
1
;
0
Maszyna cieplna zamienia nam ciepło w pracę.
Można udowodnić, że sprzęgnięcie dwóch odwracalnych maszyn cieplnych o
różnych sprawnościach daje w rezultacie perpetuum mobile drugiego rodzaju,
czyli że twierdzenie Carnota jest zgodne z drugą zasadą termodynamiki.
8
Chem. Fiz. TCH II/03
8
II Zasada Termodynamiki
(5)
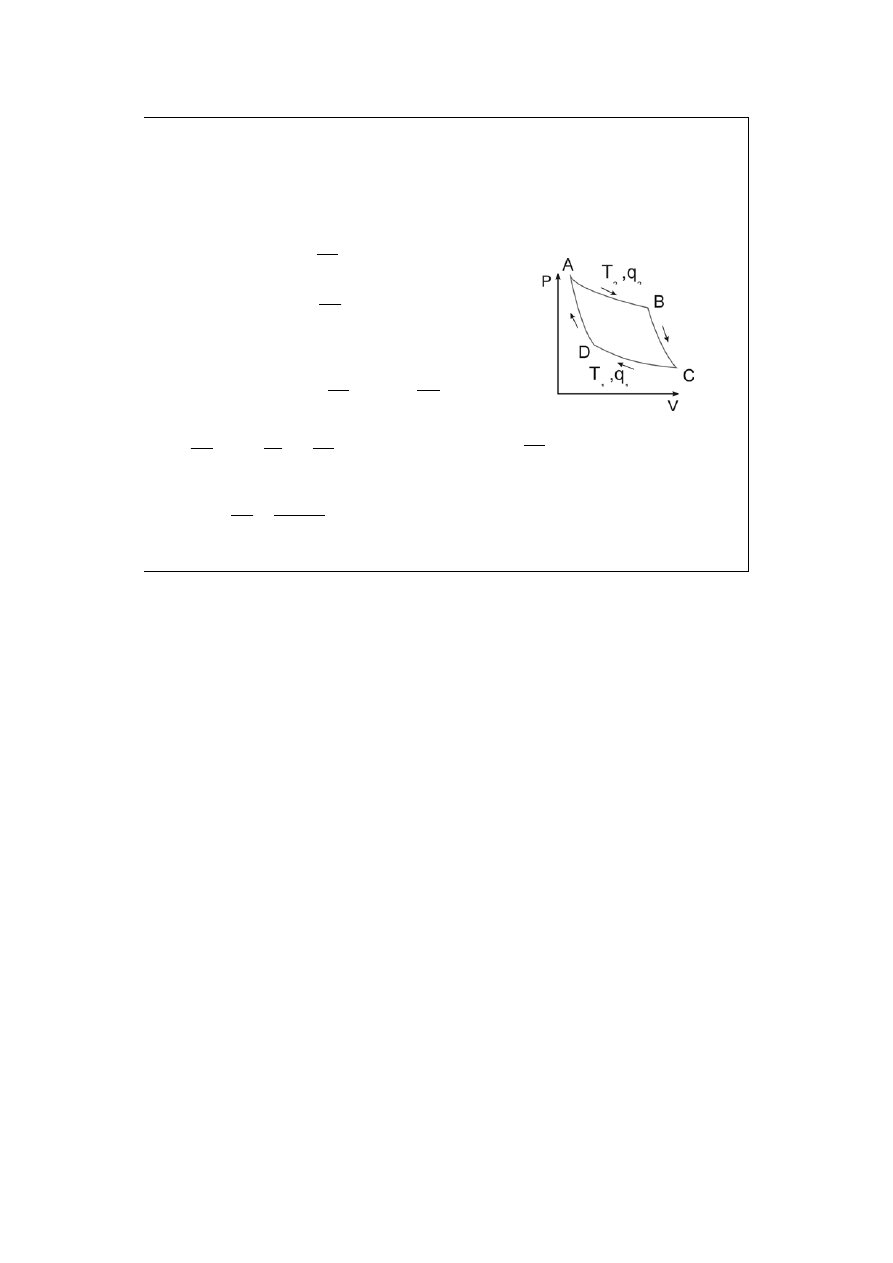
Cykl Carnota:
(1 mol gazu)
A
B
AB
V
V
RT
W
Q
ln
2
2
=
−
=
C
D
CD
V
V
RT
W
Q
ln
1
1
=
−
=
)
(
2
1
T
T
C
W
V
BC
−
=
)
(
1
2
T
T
C
W
V
DA
−
=
CD
AB
DA
CD
BC
AB
W
W
W
W
W
W
W
+
=
+
+
+
=
D
C
A
B
V
V
RT
V
V
RT
W
ln
ln
1
2
+
−
=
1
2
1
1
−
−
=
=
κ
κ
C
B
D
A
V
V
T
T
V
V
A
B
V
V
T
T
R
W
ln
)
(
2
1
−
=
2
1
2
2
T
T
T
Q
W
−
=
−
=
η
Dwie izotermy + dwie adiabaty
9
Chem. Fiz. TCH II/03
9
II Zasada Termodynamiki
(6)
0
lub
lub
2
2
1
1
2
1
2
1
2
1
2
2
2
1
=
+
−
=
−
=
+
T
Q
T
Q
T
T
Q
Q
T
T
T
Q
Q
Q
Dowolny cykl odwracalny możemy w układzie P – V przedstawić
jako sumę pewnej liczby cykli Carnota, dla której:
∑
∫
=
=
i
i
i
T
dq
T
q
0
granicznie
a
0
∫
∩
−
=
=
AB
A
B
s
s
T
dq
T
dq
ds
dalej
i
ENTROPIA
Z pierwszego równania można też wywieść identyczność absolutnej
termodynamicznej skali temperatury z absolutną skalą temperatury zdefiniowaną
w oparciu o własności gazu doskonałego.
Jeżeli całka kołowa jest równa zeru, to wyrażenie podcałkowe jest różniczką
zupełną jakiejś funkcji.
Funkcję tę nazwiemy entropią. Jest ona zatem funkcją stanu.
10
Chem. Fiz. TCH II/03
10
II Zasada Termodynamiki
(7)
Entropia układu izolowanego w procesach odwracalnych
T
dq
ds
ukł
ukł
=
Z teorematu Carnota wynika, że w procesach nieodwracalnych:
T
dq
ds
ot
ot
=
ot
ukł
dq
dq
−
=
0
=
+
=
ot
ukł
ds
ds
ds
'
'
'
2
1
2
2
2
1
T
T
T
q
q
q
−
<
+
0
'
'
2
2
1
1
<
+
T
q
T
q
∫
< 0
'
T
dq
0
'
<
+
∫
∫
∩
∩
BA
AB
T
dq
T
dq
∫
∩
>
−
AB
A
B
T
dq
s
s
'
T
dq
ds
'
>
0
)
(
,
=
v
u
ds
wreszcie:
0
>
+
ot
ukł
ds
ds
Układ zamknięty (jego otoczenie jest drugim układem zamkniętym).
Układ + otoczenie stanowią razem układ izolowany. !!!
(ds)
u,v
=0 jest kryterium równowagi układu izolowanego
11
Chem. Fiz. TCH II/03
11
II Zasada Termodynamiki
(8)
Jeśli w układzie izolowanym zachodzi proces nieodwracalny, to
entropia układu rośnie
Jeżeli w układzie izolowanym zachodzi proces odwracalny, to
entropia układu nie ulega zmianie.
0
)
(
,
≥
v
u
ds
Procesy zachodzące samorzutnie są procesami nieodwracalnymi!!!
Samorzutne są tylko te procesy, które
zwiększają entropię wszechświata
12
Chem. Fiz. TCH II/03
12
II Zasada Termodynamiki
(9)
Obliczanie zmian entropii w procesach izochorycznych:
T
dq
dS
=
Obliczanie zmian entropii w procesach izobarycznych:
PdV
dU
dq
+
=
const.
V
dla
=
=
T
dU
dS
const.
V
dla
=
=
T
dT
C
dS
V
∫
=
−
=
∆
2
1
)
(
1
2
T
T
V
dT
T
T
C
S
S
S
const.
P
dla
=
=
T
dT
C
dS
P
∫
=
−
=
∆
2
1
)
(
1
2
T
T
P
dT
T
T
C
S
S
S
13
Chem. Fiz. TCH II/03
13
II Zasada Termodynamiki
(10)
Obliczanie zmian entropii dla gazu doskonałego:
T
dq
dS
=
PdV
dU
dq
+
=
V
dV
R
T
dT
C
T
dU
dS
V
+
=
+
=
T
PdV
1
2
1
2
ln
ln
2
1
2
1
V
V
R
T
T
C
dV
V
R
dT
T
C
dV
V
R
dT
T
C
dV
V
R
dT
T
C
dV
V
R
dT
T
C
S
S
S
V
V
V
T
T
V
B
V
A
V
AB
V
p
k
+
=
+
=
+
+
+
=
+
=
−
=
∆
∫
∫
∫
∫
∫
∩
∩
∩
14
Chem. Fiz. TCH II/03
14
II Zasada Termodynamiki
(11)
Obliczanie zmian entropii dla gazu doskonałego (c.d.)
Przypadek uzależnienia od P i T:
1
2
1
2
ln
ln
P
P
R
T
T
C
S
S
S
P
p
k
−
=
−
=
∆
POMIĘDZY DWOMA DOWOLNYMI PUNKTAMI NA PŁASZCZYŹNIE P-V
MOŻNA PRZEJŚĆ JEDNĄ IZOTERMĄ I JEDNĄ IZOCHORĄ (to był
poprzedni przypadek).
PODOBNIE MOŻNA PRZEJŚĆ MIĘDZY DWOMA DOWOLNYMI
PUNKTAMI JEDNĄ IZOTERMĄ I JEDNĄ IZOBARĄ.
PROSZĘ SPRÓBOWAĆ WYPROWADZIĆ POWYŻSZY WZÓR SAMEMU
(PAMIĘTAMY O TYM ILE WYNOSI RÓŻNICA MIĘDZY C
P
I C
V
).
A WSZYSTKO TO DLATEGO, ŻE ENTROPIA JEST FUNKCJĄ STANU I
MOŻEMY SOBIE WYBRAĆ DLA SCAŁKOWANIA DOWOLNĄ DROGĘ!!!