1
Chem. Fiz. TCH II/10
1
Analiza termiczna
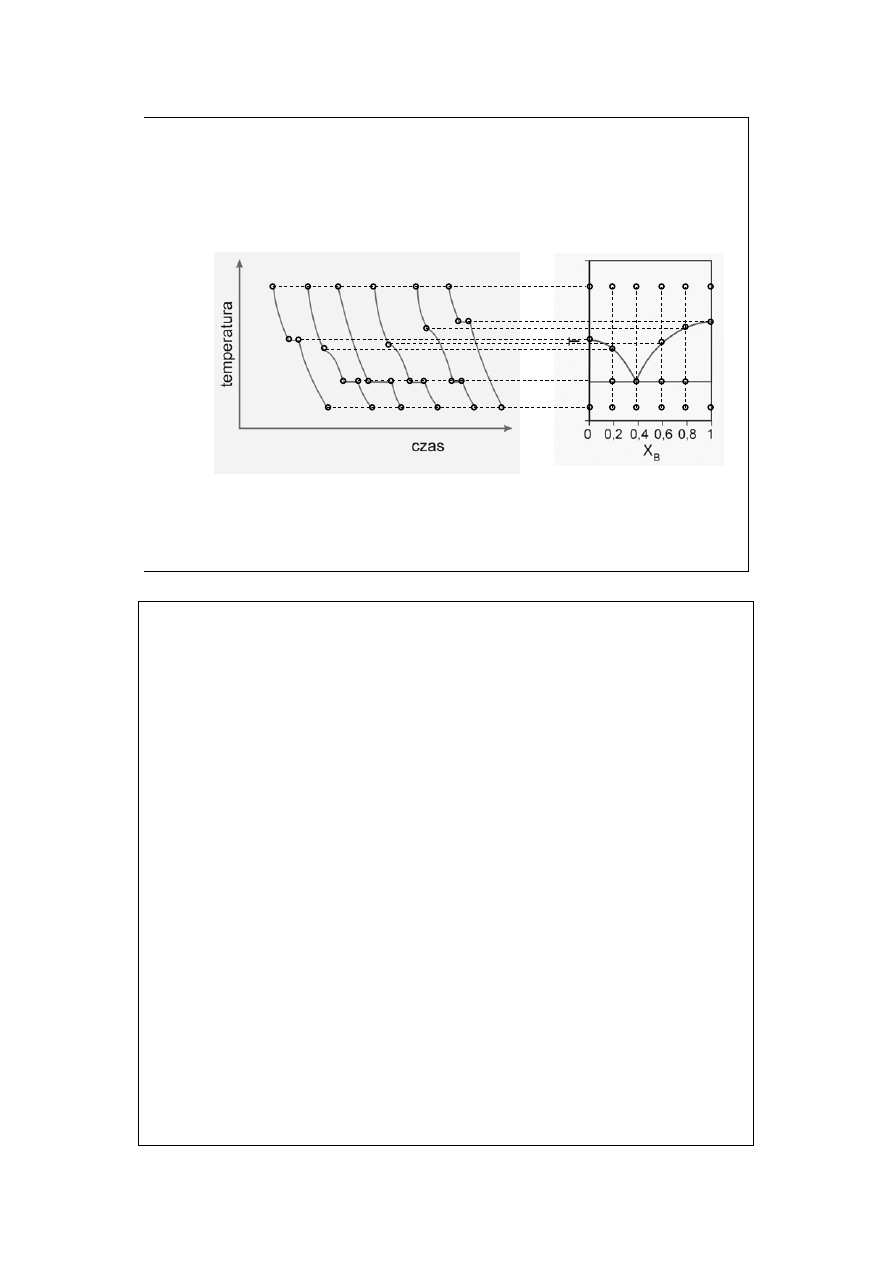
Krzywe stygnięcia
0
0,2 0,4
0,6 0,8 1,0
T
p
T
A
T
k
a
b
c
d
e
f
g h
i
j
k l
m
n
o
p
q
r
s
t
u
v
w
x
y
z
α
T
E
T
B
P = const
Rozpatrując stygnięcie wzdłuż kolejnych izoplet widzimy:
Izopleta dla X
B
=0: a-b stygnięcie cieczy; b-c krzepnięcie czystego A w
temperaturze krzepnięcia T
A
; c-d stygnięcie ciała stałego.
Izopleta dla X
B
=0,2: e-f stygnięcie cieczy; f-g stygnięcie cieczy z wydzielaniem
stałego A (punkt f odpowiada roztworowi nasyconemu) i zmianą składu cieczy;
g-h równoczesne krzepnięcie pozostałego A i pozostałego B w temperaturze
eutektycznej T
E
; h-i stygnięcie ciała stałego.
Izopleta dla X
B
=0,4: j-k stygnięcie cieczy; k-l równoczesne krzepnięcie A i B w
temperaturze eutektycznej T
E
(izopleta odpowiada składowi eutektyku) l-m
stygnięcie ciała stałego.
Izopleta dla X
B
=0,6: n-o stygnięcie cieczy; o-p stygnięcie z krystalizacją
czystego B i zmianą składu cieczy; p-q krzepnięcie eutektyku w temperaturze T
E
;
q-r stygnięcie ciała stałego.
Izopleta dla X
B
=0,8: opis identyczny jak dla izoplety X
B
=0,6.
Izopleta dla X
B
=1,0: opis identyczny jak dla izoplety X
B
=0,0 – przy czym
krzepnięcie czystego B zachodzi w temperaturze T
B
.
2
Chem. Fiz. TCH II/10
2
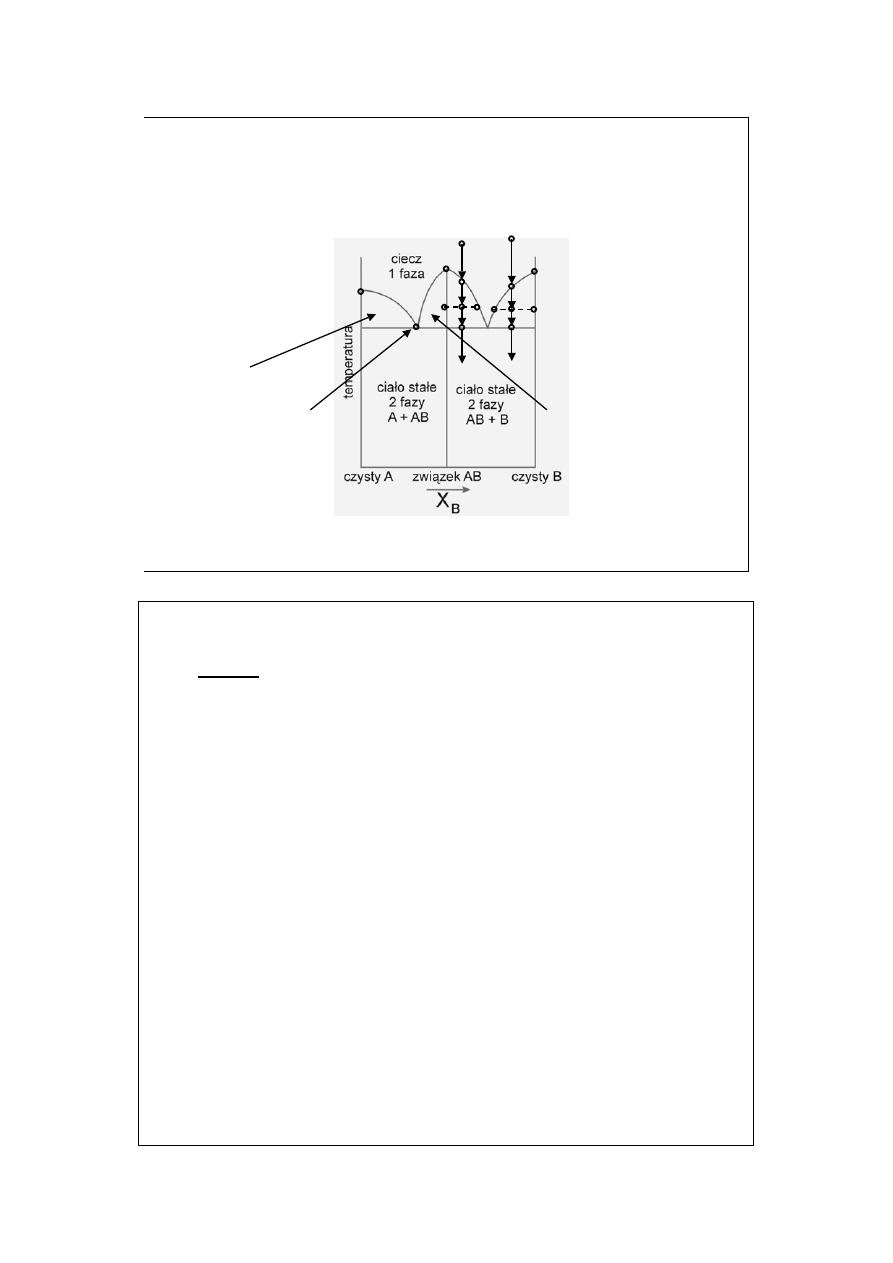
Diagramy fazowe z
tworzeniem związków (1)
T
A
T
B
T
AB
a
b
c
d
e
f
a’
b’
c’ d’
e’
f’
stałyA + ciecz
stałyAB + ciecz
eutektyk A + AB
P = const
Ga + As = GaAs
T
A
– temperatura topnienia substancji A, T
B
– temperatura topnienia substancji B,
T
AB
– temperatura topnienia związku AB.
AB to związek a nie mieszanina równomolowa!
Zwróćmy uwagę, że jest to zawsze układ dwuskładnikowy, w związku z reakcją
składniki niezależne są tylko dwa i tak też jest w każdym punkcie diagramu.
Podobny wykres opisuje układ z tworzeniem arsenku galu GaAs: Ga + As =
GaAs.
Izopleta a’-b’-c’-f’ opisuje: a’-b’ studzenie cieczy, b’-f’ stygnięcie z krystalizacją
czystego B i zmianami składu roztworu nasyconego B w ciekłym AB, w punkcie
f’ krzepnie eutektyk AB+B, poniżej f’ stygnie dwufazowe ciało stałe . Punkty d’
i e’ opisują skład obu faz w punkcie c’ (d’ – czysty B, d’ – roztwór nasycony B w
AB, wzajemne ich proporcje ilościowe opisuje reguła dźwigni).
Izopleta a-b-c-f opisuje: a-b studzenie cieczy, b-f stygnięcie z krystalizacją
związku AB i zmianami składu roztworu nasyconego AB w ciekłym B, w
punkcie f krzepnie eutektyk AB+B, poniżej f stygnie dwufazowe ciało stałe .
Punkty d i e opisują skład obu faz w punkcie c (e – czysty AB, d – roztwór
nasycony AB w B, wzajemne ich proporcje ilościowe opisuje reguła dźwigni).
3
Chem. Fiz. TCH II/10
3
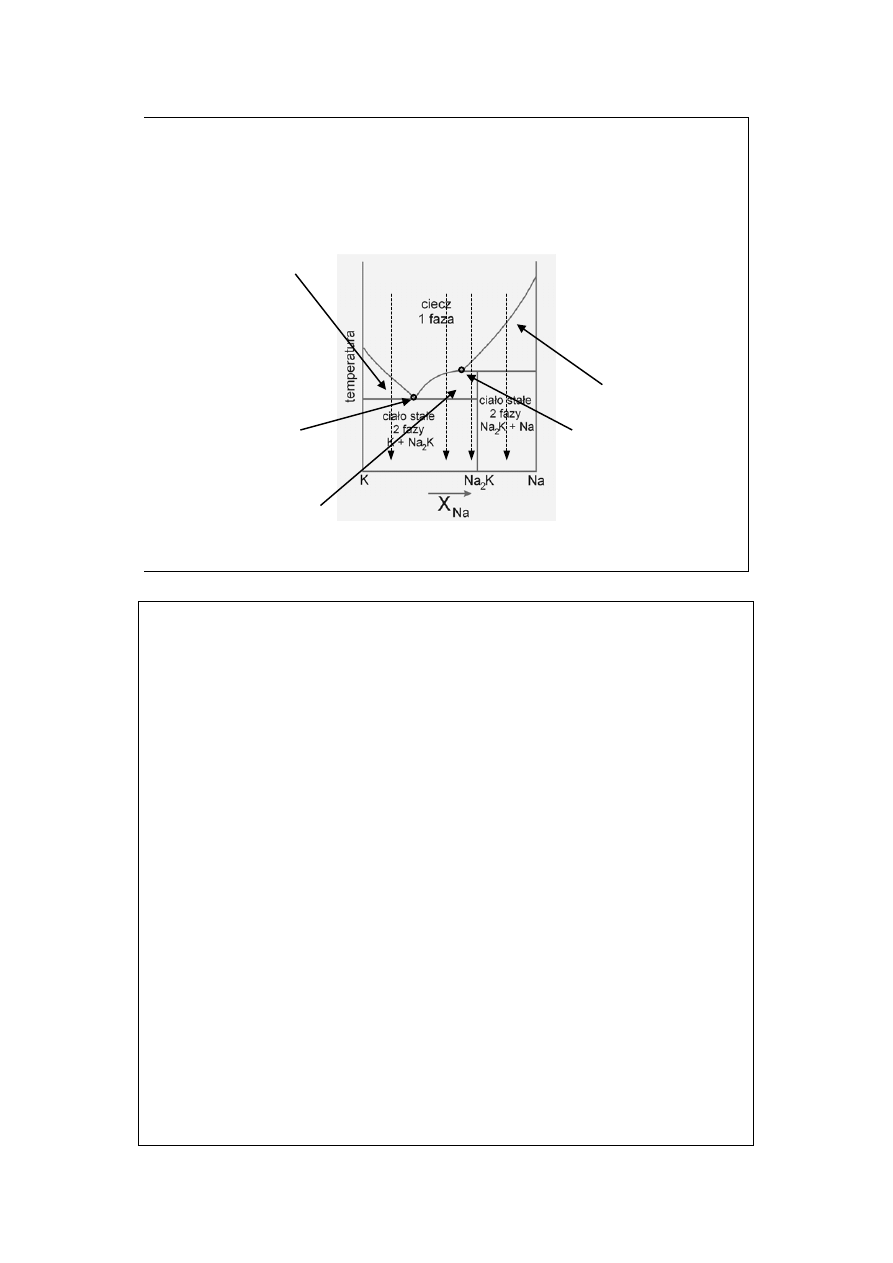
Diagramy fazowe z
tworzeniem związków (2)
Stały K + roztwór nas.
K w Na
eutektyk K + Na
2
K
Stały Na
2
K + roztwór
nas. Na
2
K w K
Stały Na + roztwór
nas. Na w K
Topnienie niekongruentne
a
b
c
d
Topnienie niekongruentne, Na
2
K nie istnieje w fazie ciekłej!
Spróbujmy omówić krzywe stygnięcia wzdłuż izoplet a, b i c. A jak to będzie
wzdłuż d?
4
Chem. Fiz. TCH II/10
4
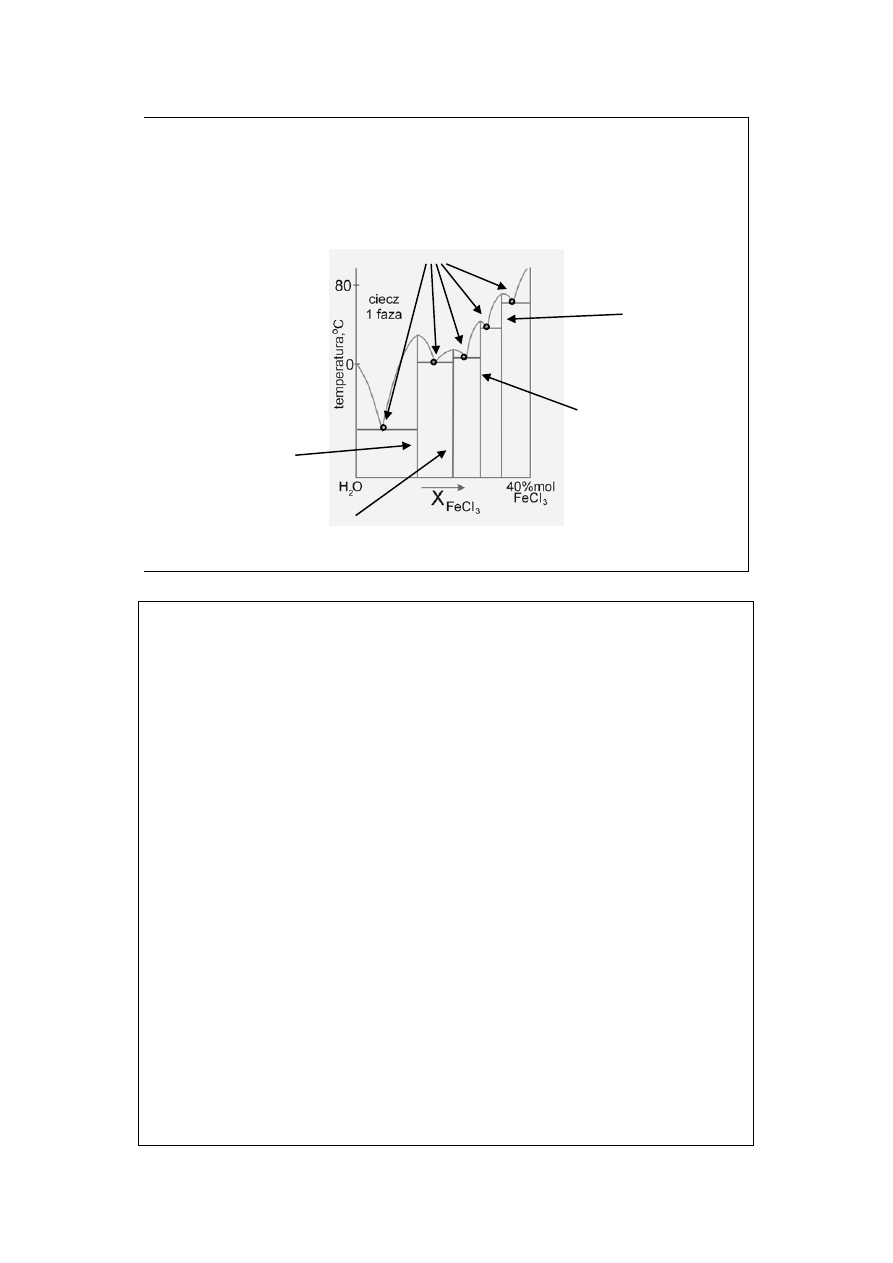
Diagramy fazowe z
tworzeniem związków (3)
eutektyki
FeCl
3
•6H
2
O
FeCl
3
•3½H
2
O
FeCl
3
•2½H
2
O
FeCl
3
•2H
2
O
Istnieją tu cztery różne hydraty stałe. Jakie równowagi tworzą one z wodą ciekłą
(roztworami FeCl
3
w wodzie lub wody w FeCl
3
)?
5
Chem. Fiz. TCH II/10
5
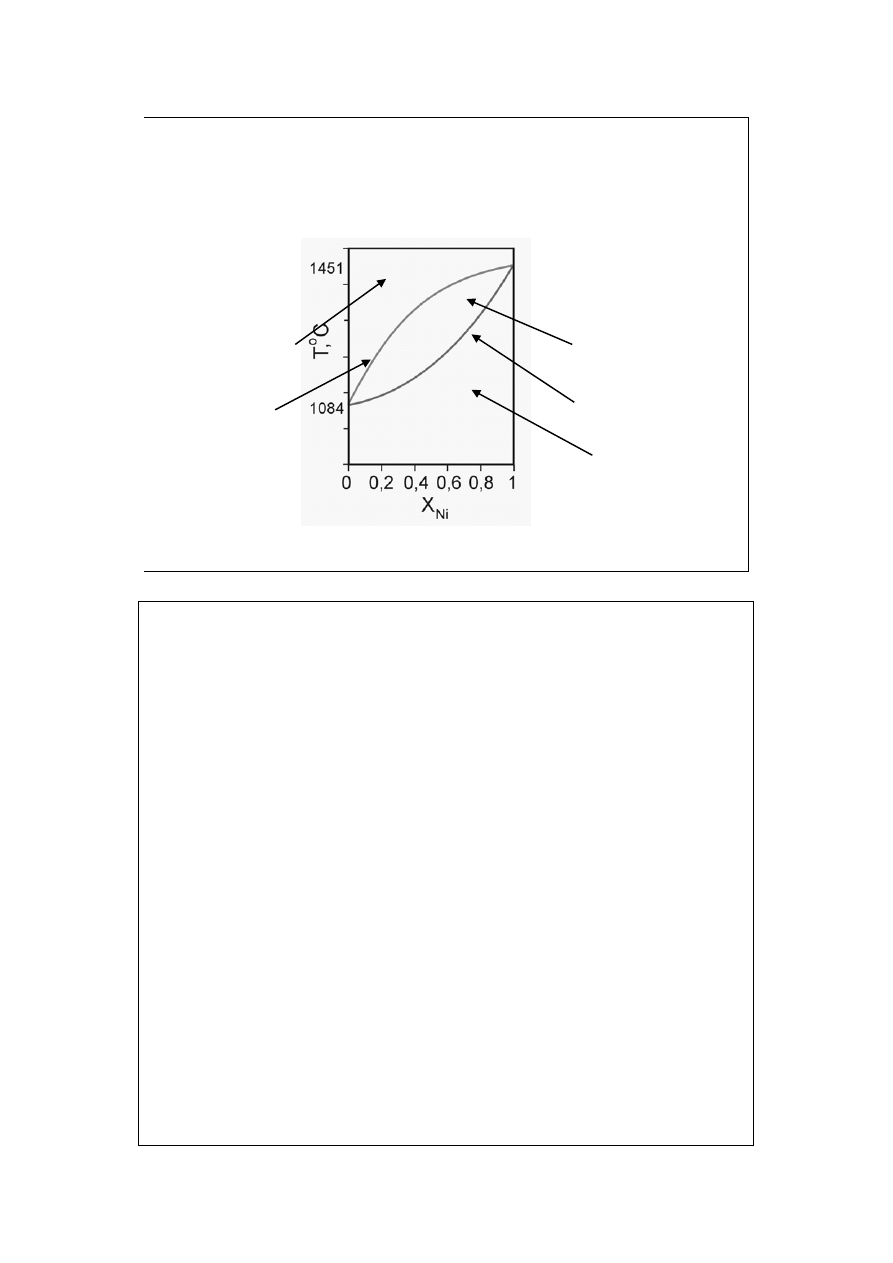
Diagramy fazowe
z roztworami stałymi (1)
solidus
Roztwór ciekły
1 faza
solidus
Roztwór stały
1 faza
obszar współ-
istnienia faz
Cu-Ni
Rzadki przypadek nieograniczonej wzajemnej rozpuszczalności w fazie stałej!
6
Chem. Fiz. TCH II/10
6
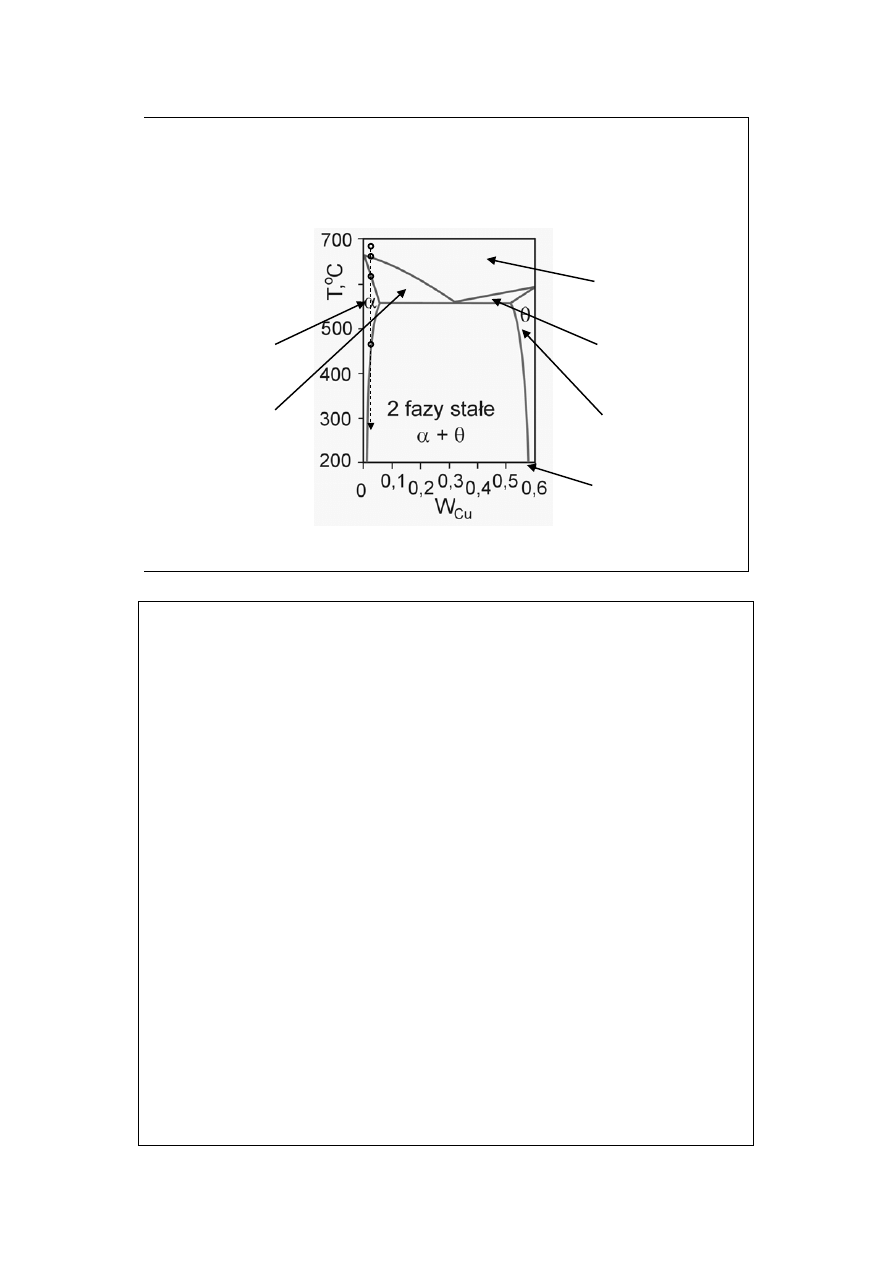
Diagramy fazowe
z roztworami stałymi (2)
obszar współ-
istnienia cieczy
i fazy stałej α
Roztwór stały
(CuAl
2
w Cu)
1 faza
ciecz
CuAl
2
(58%Cu)
obszar współ-
istnienia cieczy
i fazy stałej θ
Cu-Al
Roztwór stały
(Cu w CuAl
2
)
1 faza
a
Ograniczona wzajemna rozpuszczalność w fazie stałej.
Rozważmy krzywą stygnięcia wzdłuż izoplety a. W jej ostatnim punkcie (licząc
w dół) pojawi się faza θ. Ale będzie to raczej metastabilna (powolne przemiany
w fazie stałej), przechłodzona faza α (miękka i plastyczna). Z upływem czasu
dojdzie do hartowania stopu przez starzenie.
7
Chem. Fiz. TCH II/10
7
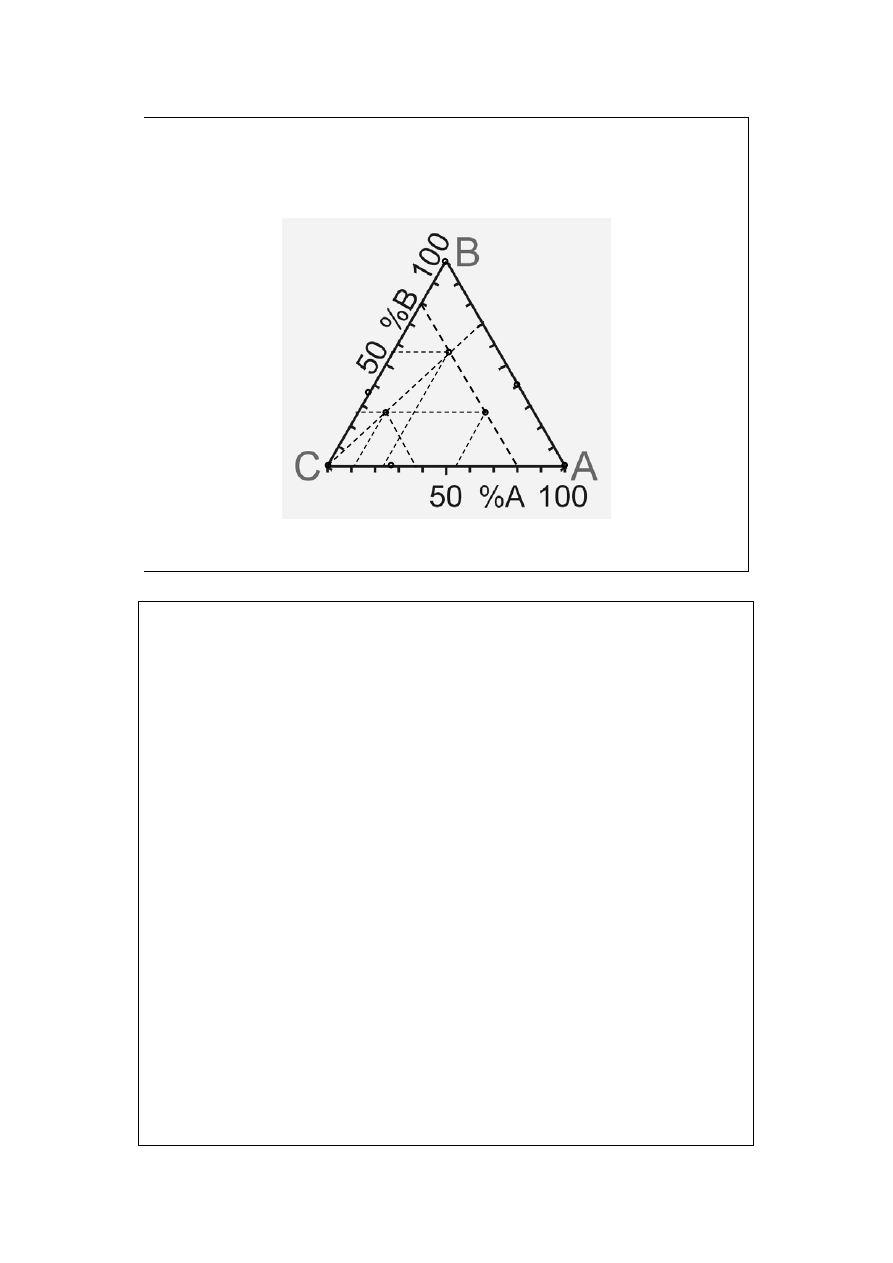
Układy trójskładnikowe (1).
Trójkąt Gibbsa
a
b
c
f + p = 5
d
d’
d”
Punkty w wierzchołkach oznaczonych literami oznaczają układy
jednoskładnikowe (czyste składniki A, B i C).
Punkty na liniach przeciwległych wierzchołkom A, B i C oznaczają układy
dwuskładnikowe o zerowej zawartości składnika A, B lub C.
Np. punkt a odpowiada 60%A, 40%B i 0%C (%A+%B+%C=100); punkt b
odpowiada 0%A, 36%B i 64%C; punkt c odpowiada 28%A, 0%B i 72%C.
Punkty leżące na liniach równoległych do boku przeciwległego do wierzchołków
A, B i C odpowiadają stałej zawartości składnika A, B lub C.
Np. punkty d i d’ odpowiadają składom po 20% składnika C (d ma poza tym
56%B i 24%A; d’ ma 26%B i 54%A).
Punkty leżące na liniach wychodzących z wierzchołka A, B lub C oznaczają
składy o stałej proporcji pozostałych dwóch składników.
Np. punkty d i d”. (d ma proporcję A:B równą 24:56=3:7=0,43 i dodatkowo
20%C; zaś d” – 11,1:26=0,43 i dodatkowo zawiera 62,9%C).
8
Chem. Fiz. TCH II/10
8
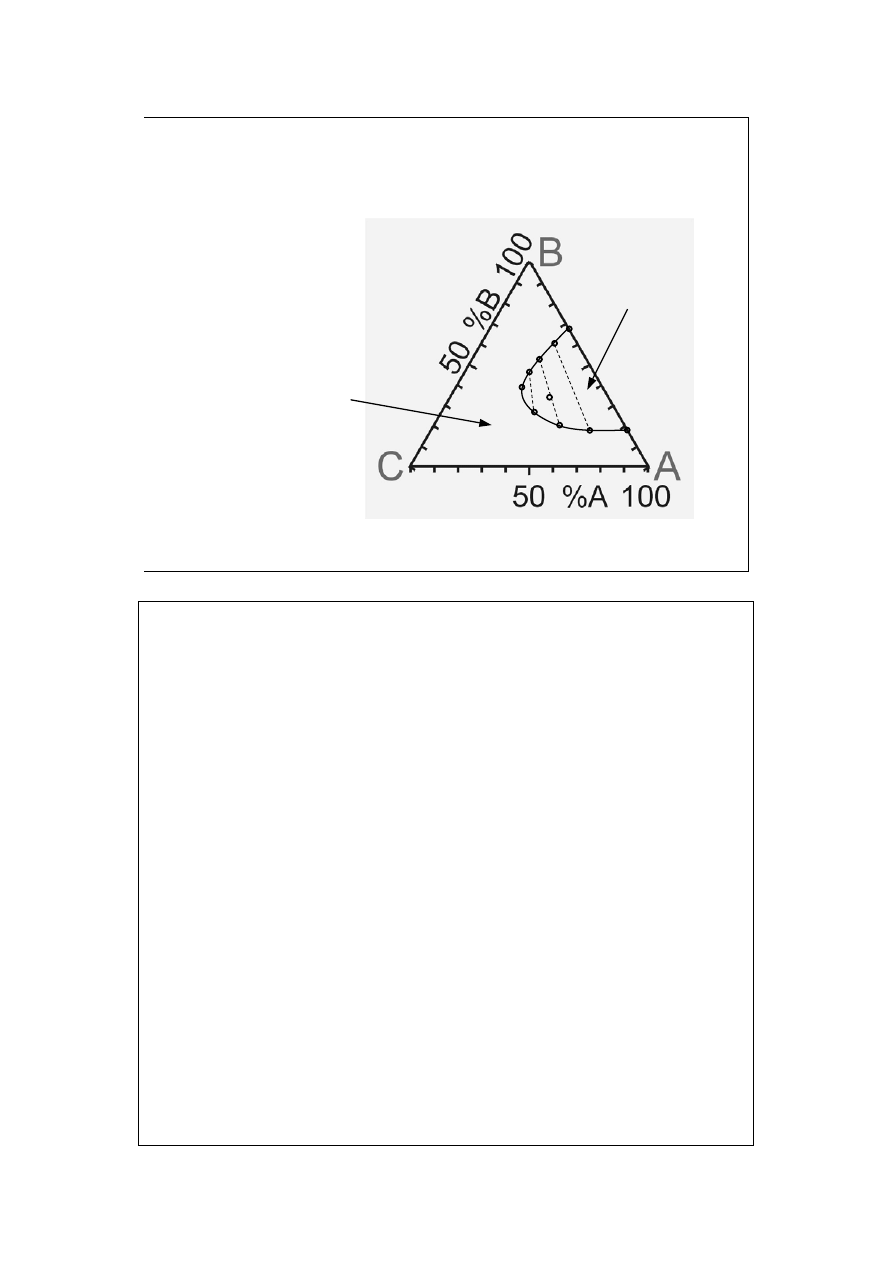
Układy trójskładnikowe (2).
a
b
d
A i B wykazują
ograniczoną wzajemną
rozpuszczalność
P=const, T=const
c
f
e
g
h
S
1 faza ciekła
2 fazy ciekłe
i
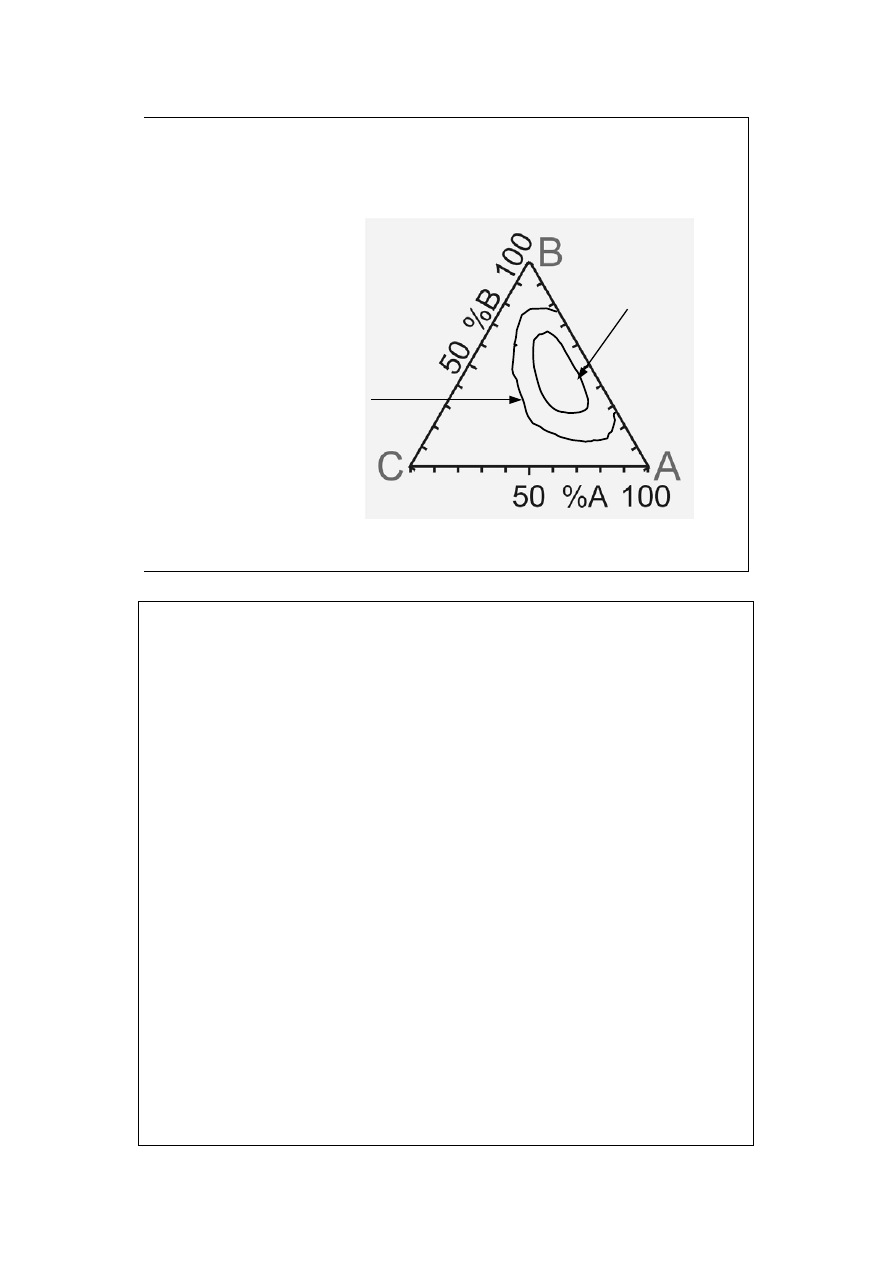
Pozostałe dwie pary (B i C oraz A i C) rozpuszczają się w danych warunkach bez
ograniczeń.
Pomarańczowa krzywa nosi nazwę krzywej binodalnej. Linie łączące pary
punktów a-b, c-d, e-f i g-h zwane są liniami wiążącymi lub konodami. Punkt S
nosi nazwę punktu splotu. Dla pełnej charakterystyki (aby znaleźć punkty
odpowiadające składom obu faz pozostających w równowadze wewnątrz obszaru
ograniczonego krzywą binodalną) konieczna jest znajomość konod.
Od linii a-b (oba składniki A i B tworzą dwie fazy) przechodzimy do kolejnych
konod dodając składnika C i analizując fazy.
Punkty a, c, e, g odpowiadają roztworowi nasyconemu A w cieczy złożonej z
dwóch pozostałych składników (lub tylko B w punkcie a).
Punkty b, d, f, h odpowiadają roztworowi nasyconemu B w cieczy złożonej z
dwóch pozostałych składników (lub tylko A w punkcie b).
Punkty leżące na konodach (np. i) dzielą się na obie fazy zgodnie z regułą
dźwigni.
Punkt S odpowiada roztworowi nasyconemu gdy dwie fazy mają identyczny
skład, jest to roztwór nasycony owej jednej fazy A-B w C.
9
Chem. Fiz. TCH II/10
9
Układy trójskładnikowe (3).
A i B wykazują
ograniczoną wzajemną
rozpuszczalność
P=const, T=const
30
o
C
80
o
C
A = C
6
H
5
OH
B = H
2
O
C = (CH
3
)
2
CO
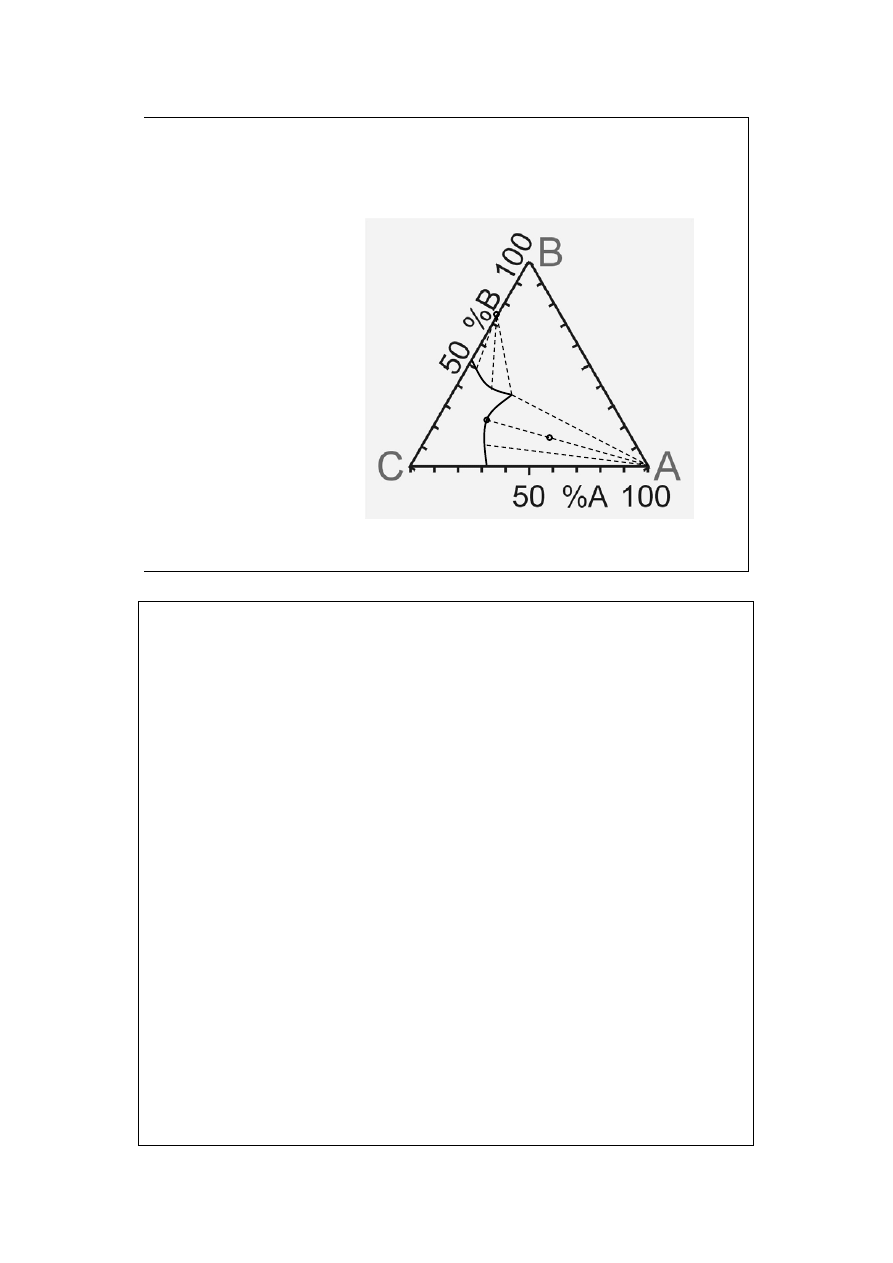
Powyżej pewnej temperatury wszystkie 3 ciecze mieszają się ze sobą w
dowolnym stosunku.
Przekroje przez trójwymiarowe wykresy (wiele ułożonych na sobie trójkątów
Gibbsa, każdy – w górę – przy coraz wyższej temperaturze) są często stosowane.
Izotermy stanowią wtedy na nich warstwice. Można przedstawiać na nich np.
układy trójskładnikowe z fazami stałymi.
10
Chem. Fiz. TCH II/10
10
Układy trójskładnikowe (4).
P=const, T=const
A = sól1
B = sól2 (wspólny jon z A)
C = H
2
O
R
S
Z
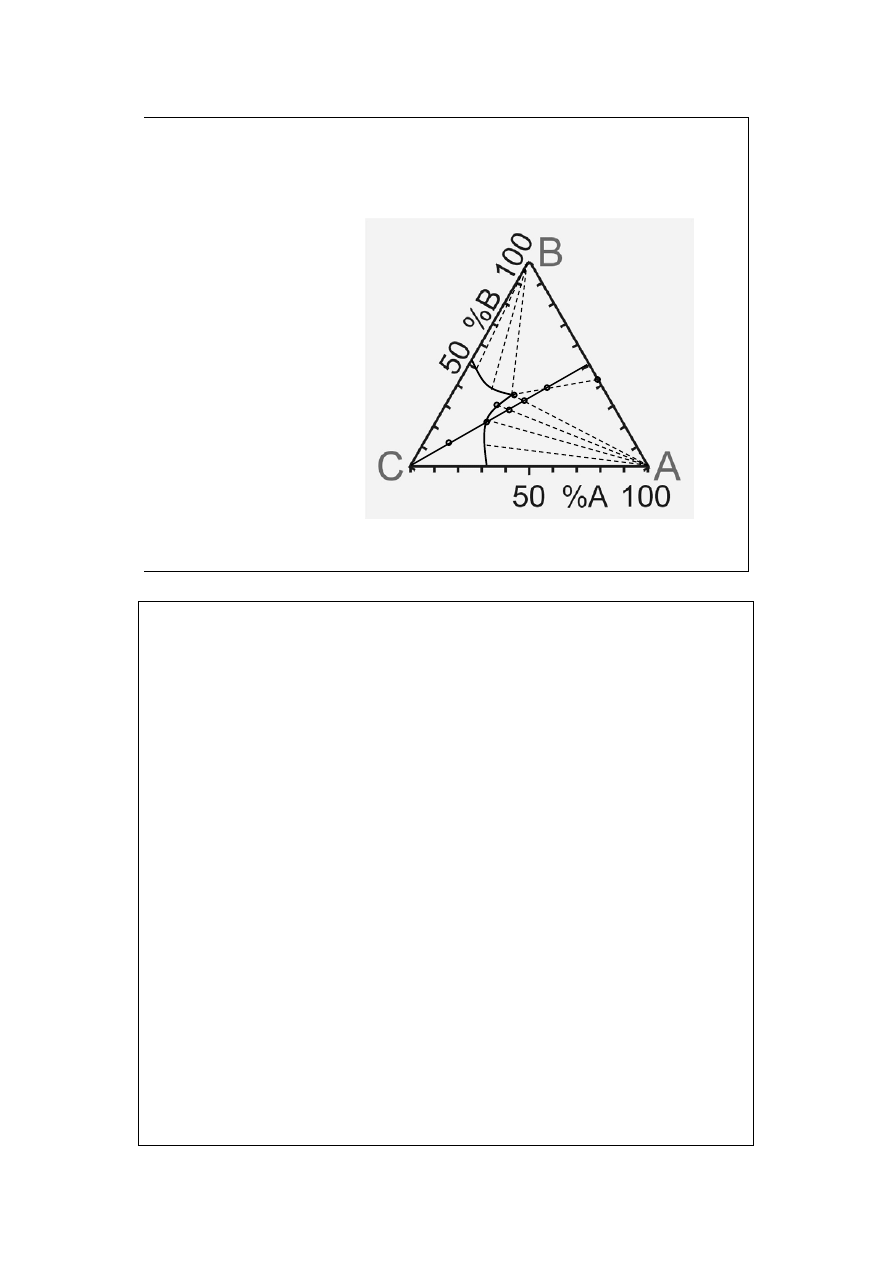
Punkt R wyznaczamy z analizy Roztworu nasyconego. Punkt S z analizy składu
Sumarycznego. Jeżeli konoda przechodzi przez wierzchołek A, to znaczy, że
składnikiem stałym jest czysta sól 1 (można oczywiście wyznaczyć więcej konod
dla dokładności i uzyskania pewności).
Jeżeli pierwsza konoda nie przechodzi przez wierzchołek, to trzeba wyznaczyć
więcej konod. W podanym przykładzie ich punkt zbieżności Z wskazuje, że
drugą fazę stałą stanowi hydrat soli 2.
11
Chem. Fiz. TCH II/10
11
Układy trójskładnikowe (5).
P=const, T=const
A = sól1
B = sól2 (wspólny jon z A)
C = H
2
O
l
m
o
w
n
x y
z
Izotermicznie odparowujemy wodę. Od punktu l do m mamy do czynienia z
roztworem nienasyconym. W m istnieje już nasycony soli A. Od m do x wydziela
się stała sól 1, zaś roztwór nasycony zmienia skład od m przez n do o.
Począwszy od punktu o wydzielają się już obie sole równocześnie. Jeżeli skład
całkowity jest y, to skład wydzielających się soli określa nam punkt z.
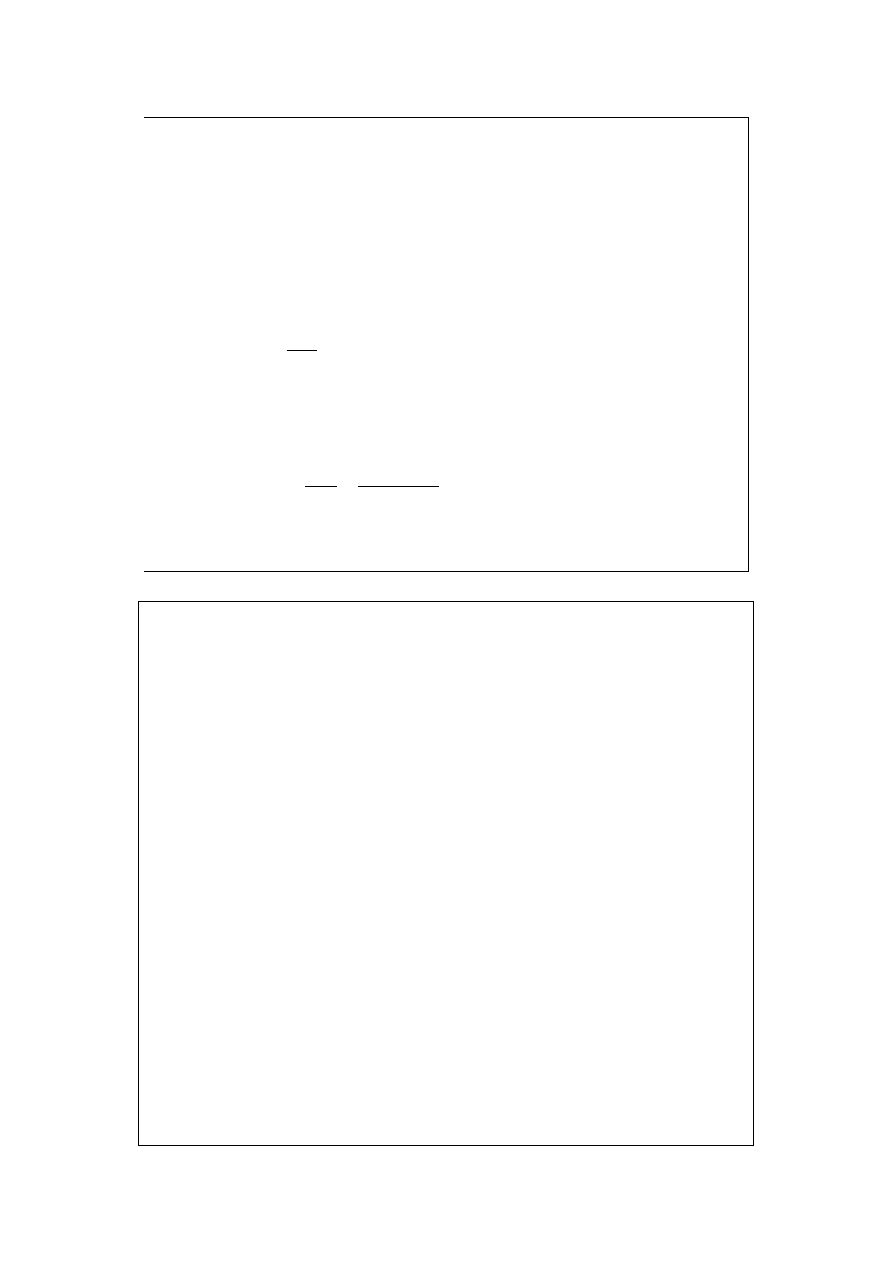
12
Chem. Fiz. TCH II/10
12
Prawo podziału Nernsta
Dwa składniki (ciecze) o ograniczonej wzajemnej rozpuszczalności
a trzeci składnik (ciecz) obecny w bardzo niewielkich ilościach.
Stwierdzono empirycznie, że:
n
const
c
c
II
I
=
=
,
3
,
3
jeżeli P i T = const
Termodynamicznie:
II
I
,
3
,
3
µ
µ
=
zatem:
II
II
I
I
a
RT
a
RT
,
3
0
,
3
,
3
0
,
3
ln
ln
+
=
+
µ
µ
a także:
RT
a
a
I
II
II
I
0
,
3
0
,
3
,
3
,
3
ln
µ
µ
−
=
= const gdy T=const
Opisywany przypadek ma wielkie znaczenie praktyczne (chromatografia
cieczowa!!!).
n nie zależy od stosunku ilościowego obu faz (I i II) i całkowitej (niewielkiej)
ilości substancji 3.
Widać z ostatniego równania, że prawo podziału w postaci ze stężeniami jest
prawem granicznym, bowiem musimy móc założyć, że współczynniki
aktywności substancji 3 w obu fazach są równe 1.