Chem. Fiz. TCH II/10

1

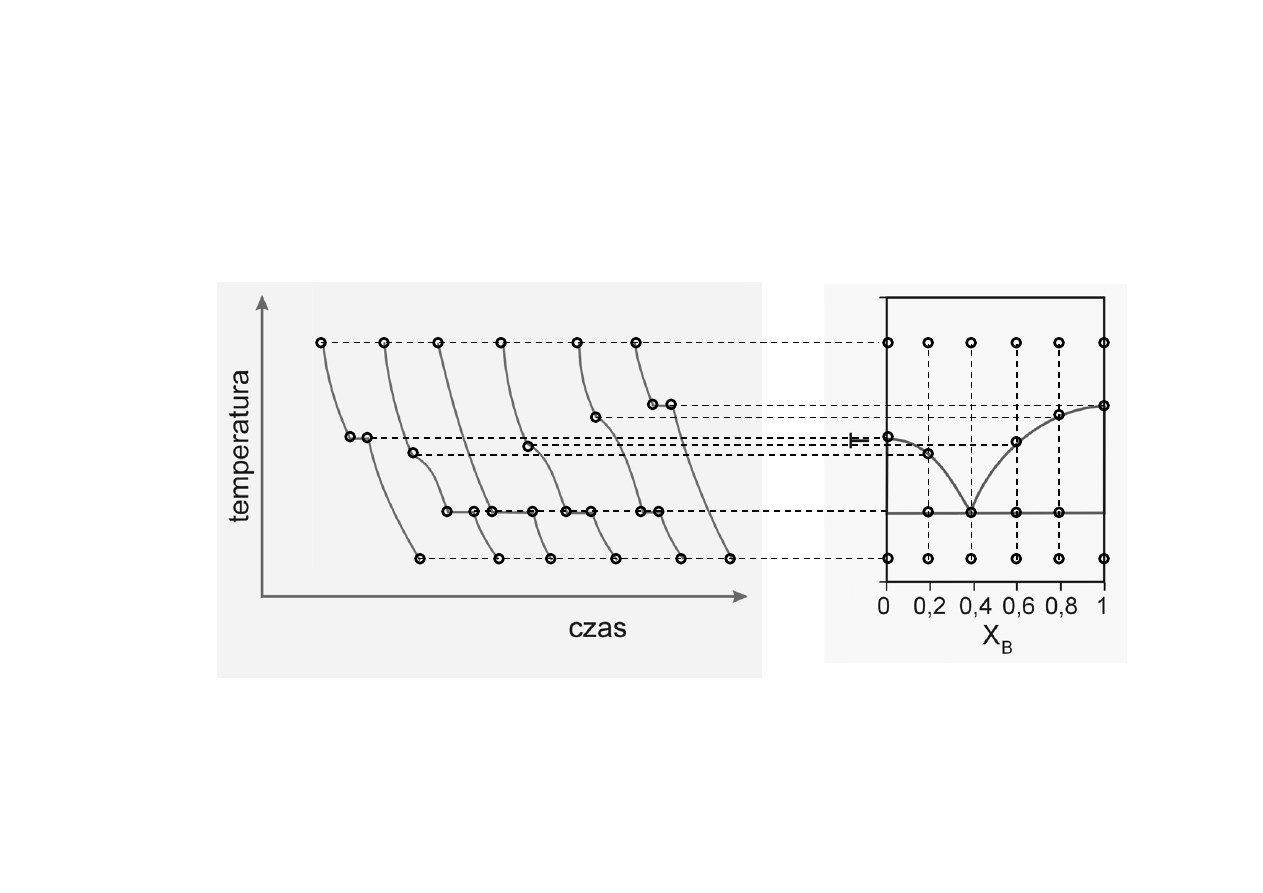
Analiza termiczna

Krzywe stygnięcia

0

0,2 0,4

0,6 0,8 1,0

T

p

T

A

T

k

a

b

c

d

e

f

g h

i

j

k l

m

n

o

p

q

r

s

t

u

v

w

x

y

z

α

T

E

T

B

P = const

Chem. Fiz. TCH II/10

2

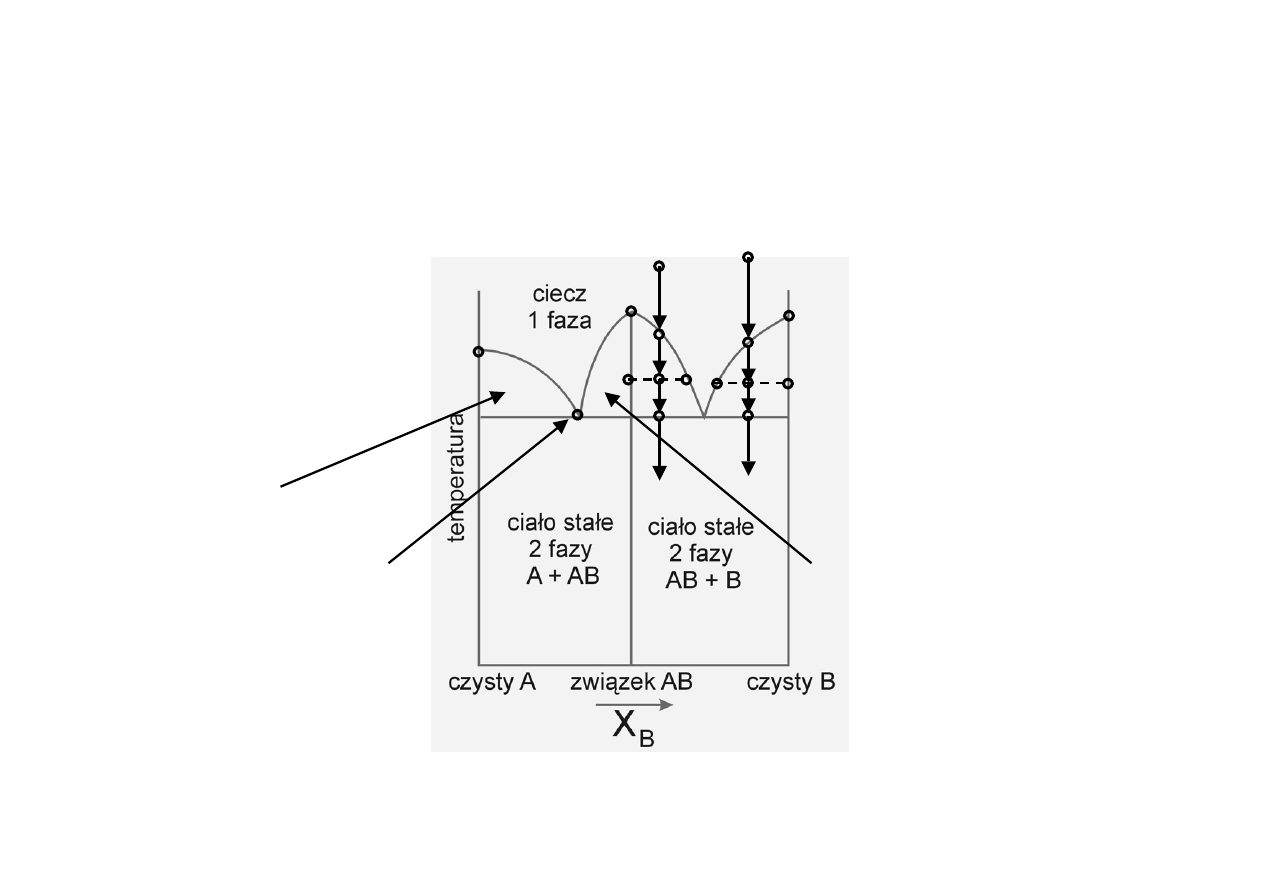
Diagramy fazowe z

tworzeniem związków (1)

T

A

T

B

T

AB

a

b

c

d

e

f

a’

b’

c’ d’

e’

f’

stałyA + ciecz

stałyAB + ciecz

eutektyk A + AB

P = const

Ga + As = GaAs

Chem. Fiz. TCH II/10

3

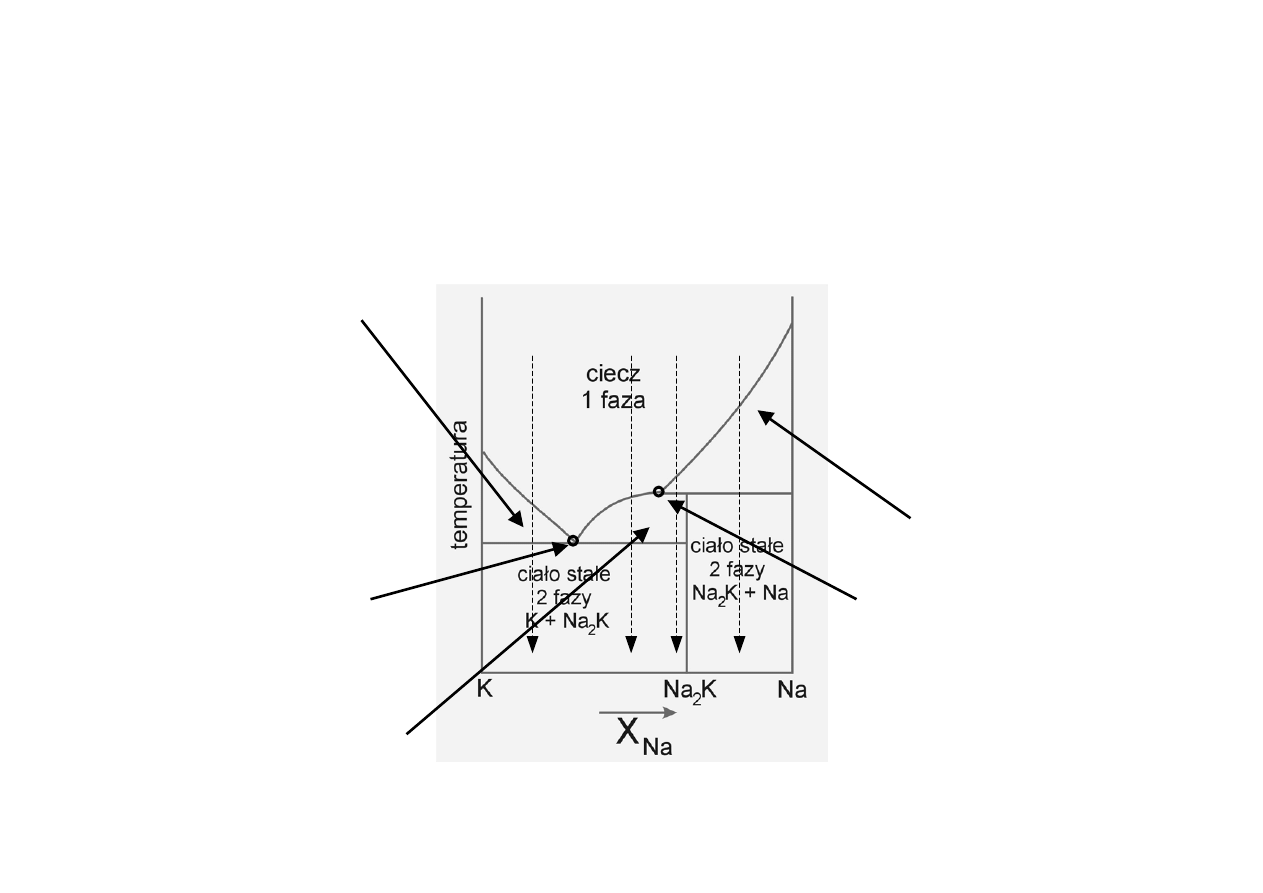
Diagramy fazowe z

tworzeniem związków (2)

Stały K + roztwór nas.

K w Na

eutektyk K + Na

2

K

Stały Na

2

K + roztwór

nas. Na

2

K w K

Stały Na + roztwór

nas. Na w K

Topnienie niekongruentne

a

b

c

d

Chem. Fiz. TCH II/10

4

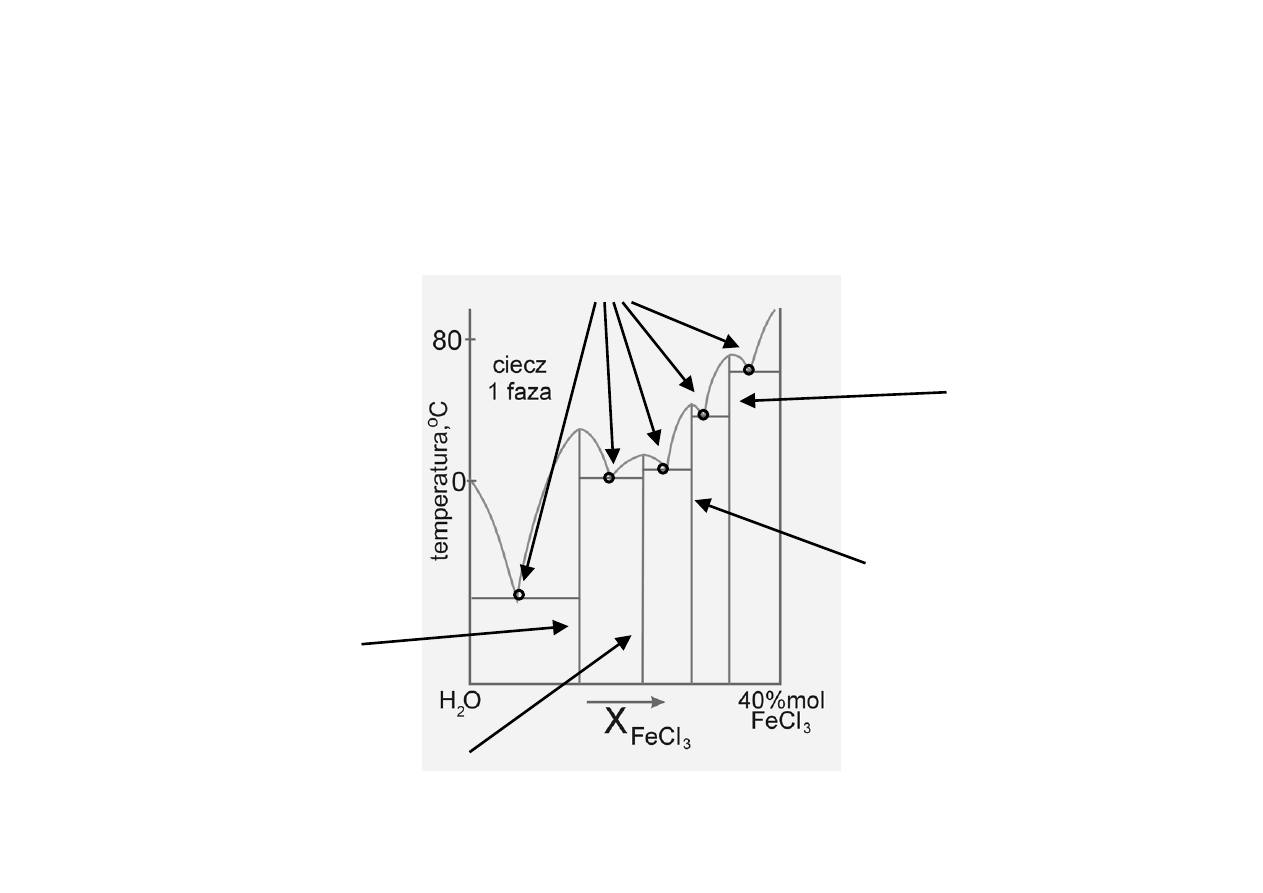
Diagramy fazowe z

tworzeniem związków (3)

eutektyki

FeCl

3

•6H

2

O

FeCl

3

•3½H

2

O

FeCl

3

•2½H

2

O

FeCl

3

•2H

2

O

Chem. Fiz. TCH II/10

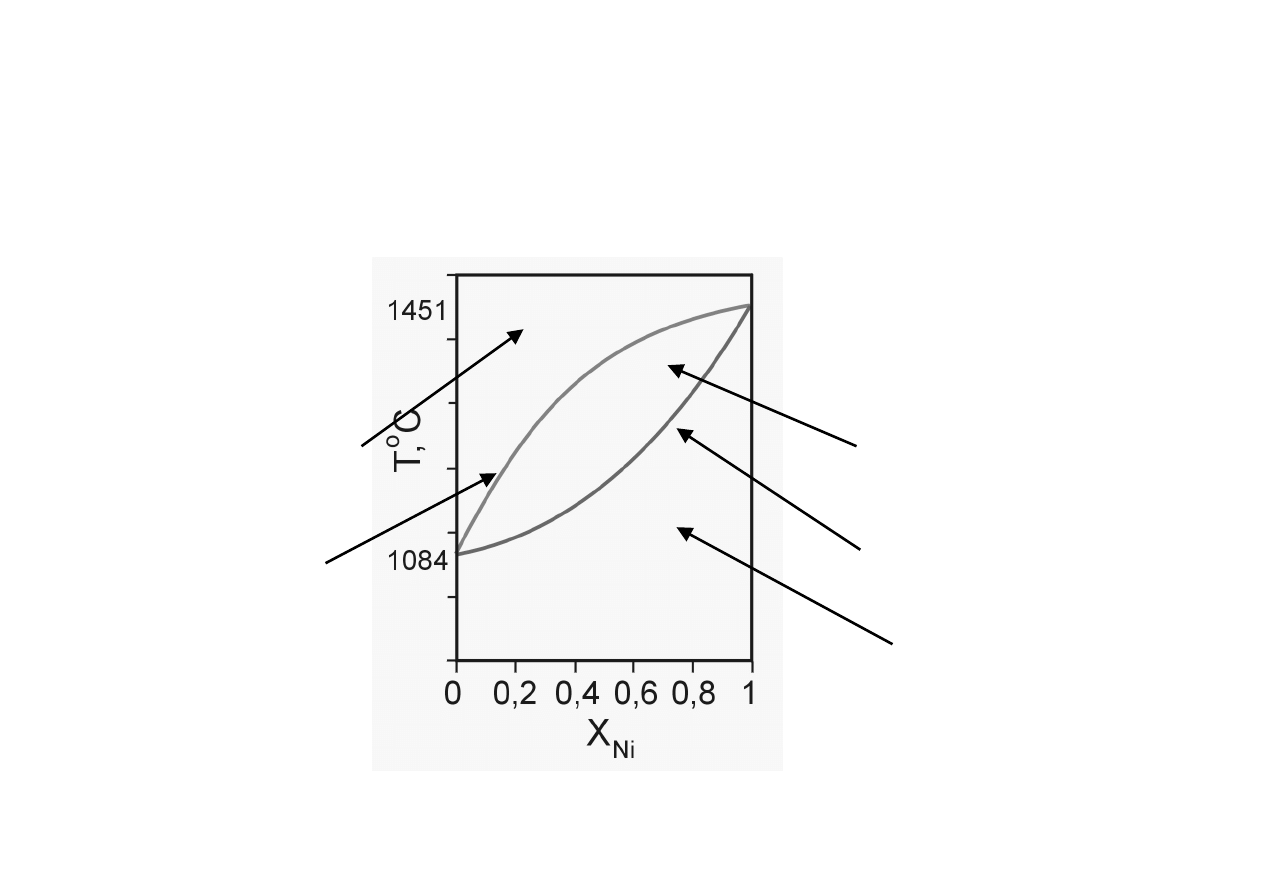
5

Diagramy fazowe

z roztworami stałymi (1)

solidus

Roztwór ciekły

1 faza

solidus

Roztwór stały
1 faza

obszar współ-
istnienia faz

Cu-Ni

Chem. Fiz. TCH II/10

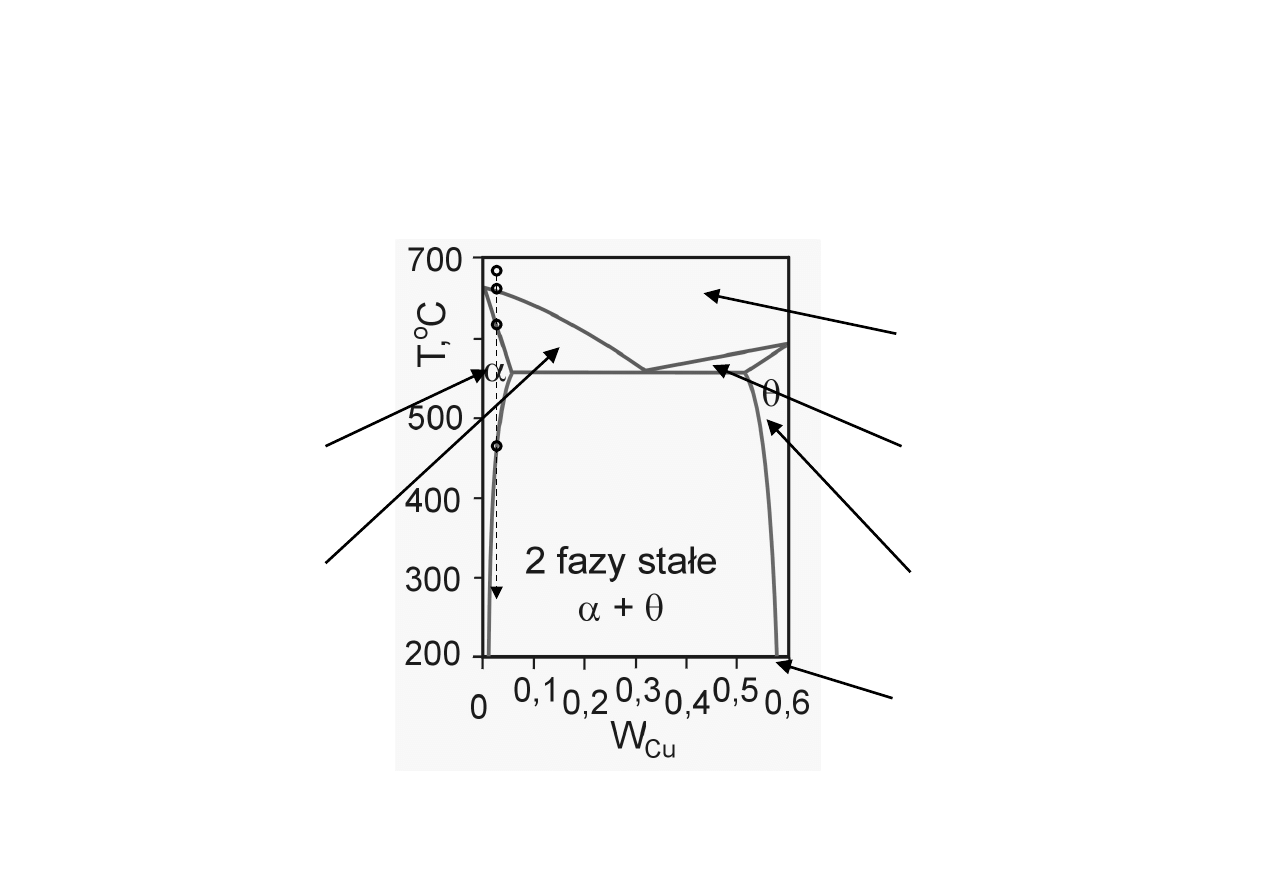
6

Diagramy fazowe

z roztworami stałymi (2)

obszar współ-

istnienia cieczy

i fazy stałej α

Roztwór stały

(CuAl

2

w Cu)

1 faza

ciecz

CuAl

2

(58%Cu)

obszar współ-
istnienia cieczy
i fazy stałej θ

Cu-Al

Roztwór stały
(Cu w CuAl

2

)

1 faza

a

Chem. Fiz. TCH II/10

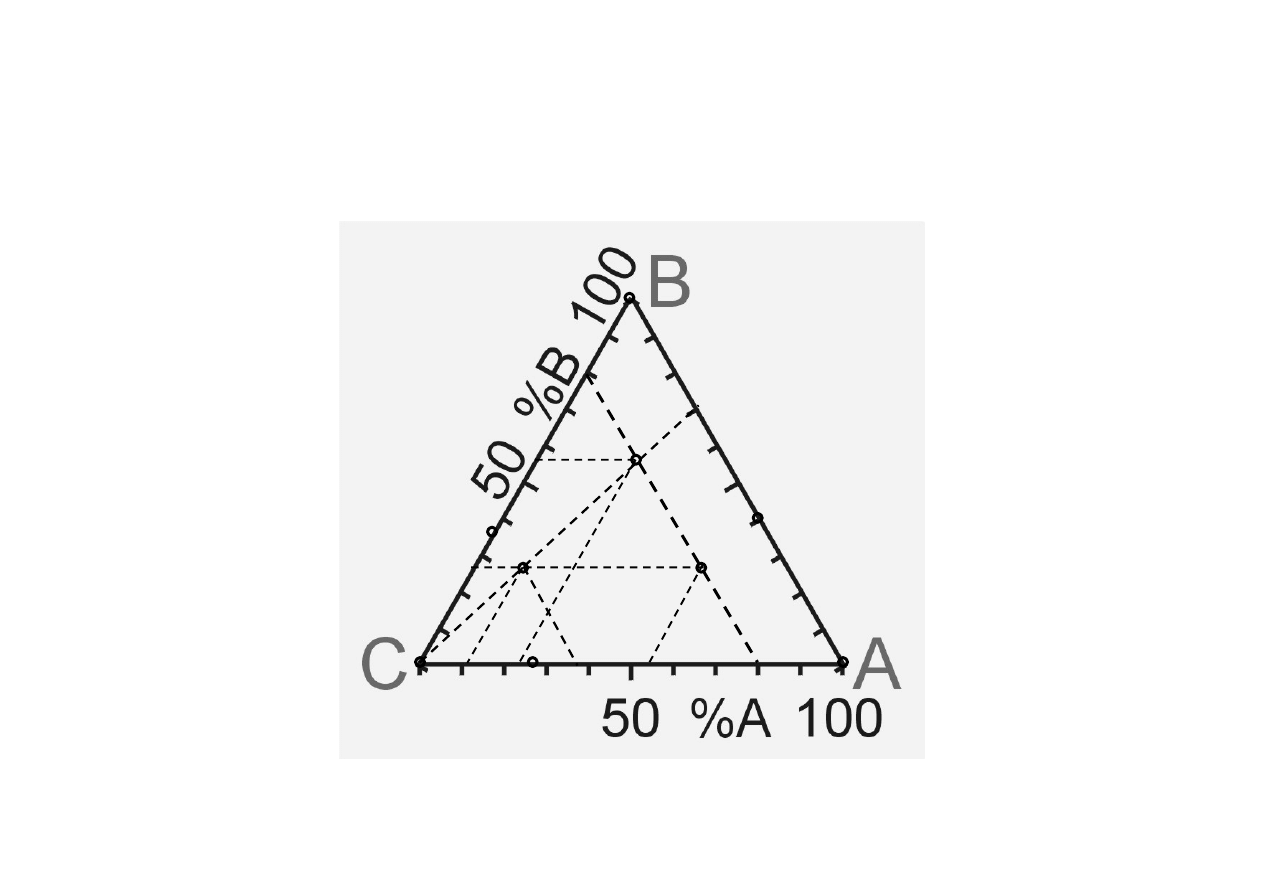
7

Układy trójskładnikowe (1).

Trójkąt Gibbsa

a

b

c

f + p = 5

d

d’

d”

Chem. Fiz. TCH II/10

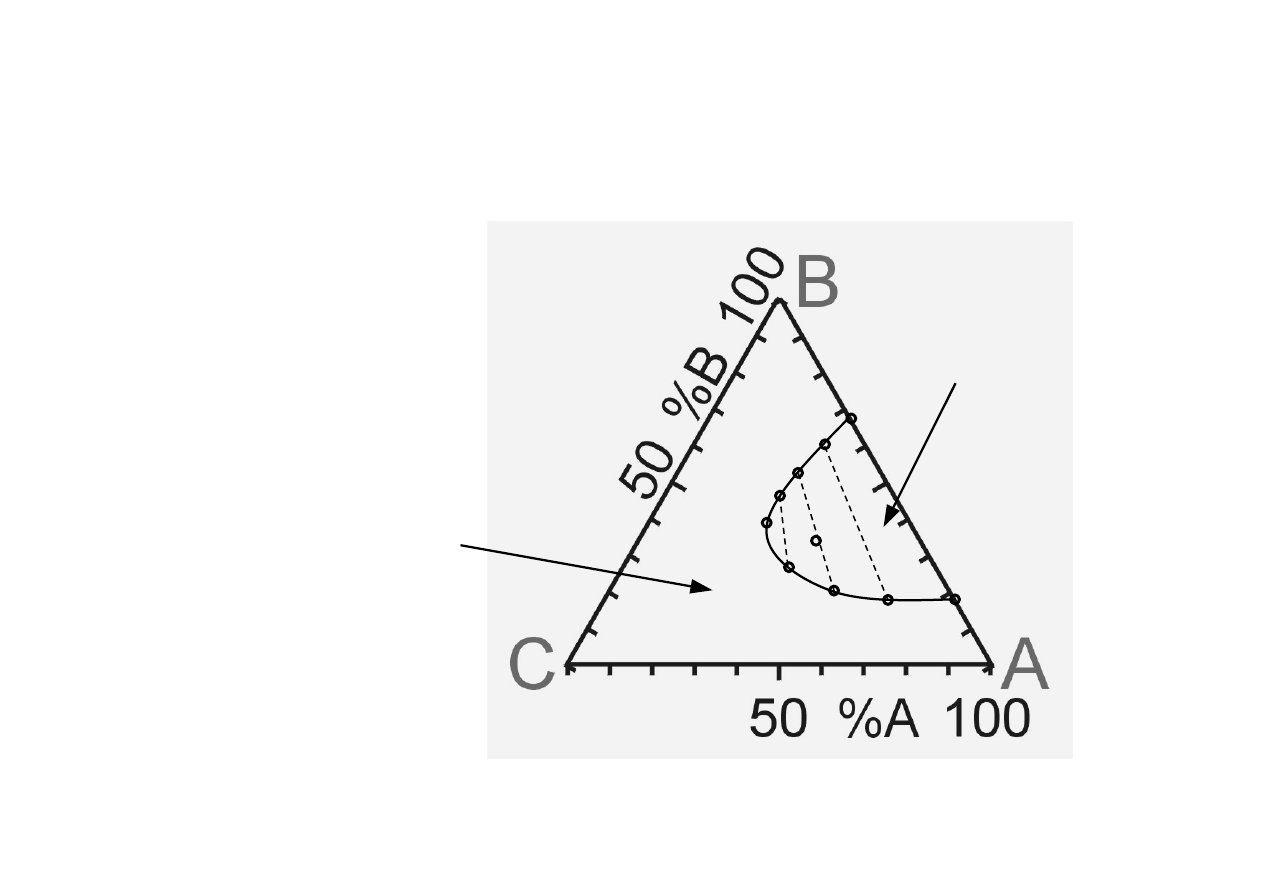
8

Układy trójskładnikowe (2).

a

b

d

A i B wykazują

ograniczoną wzajemną

rozpuszczalność

P=const, T=const

c

f

e

g

h

S

1 faza ciekła

2 fazy ciekłe

i

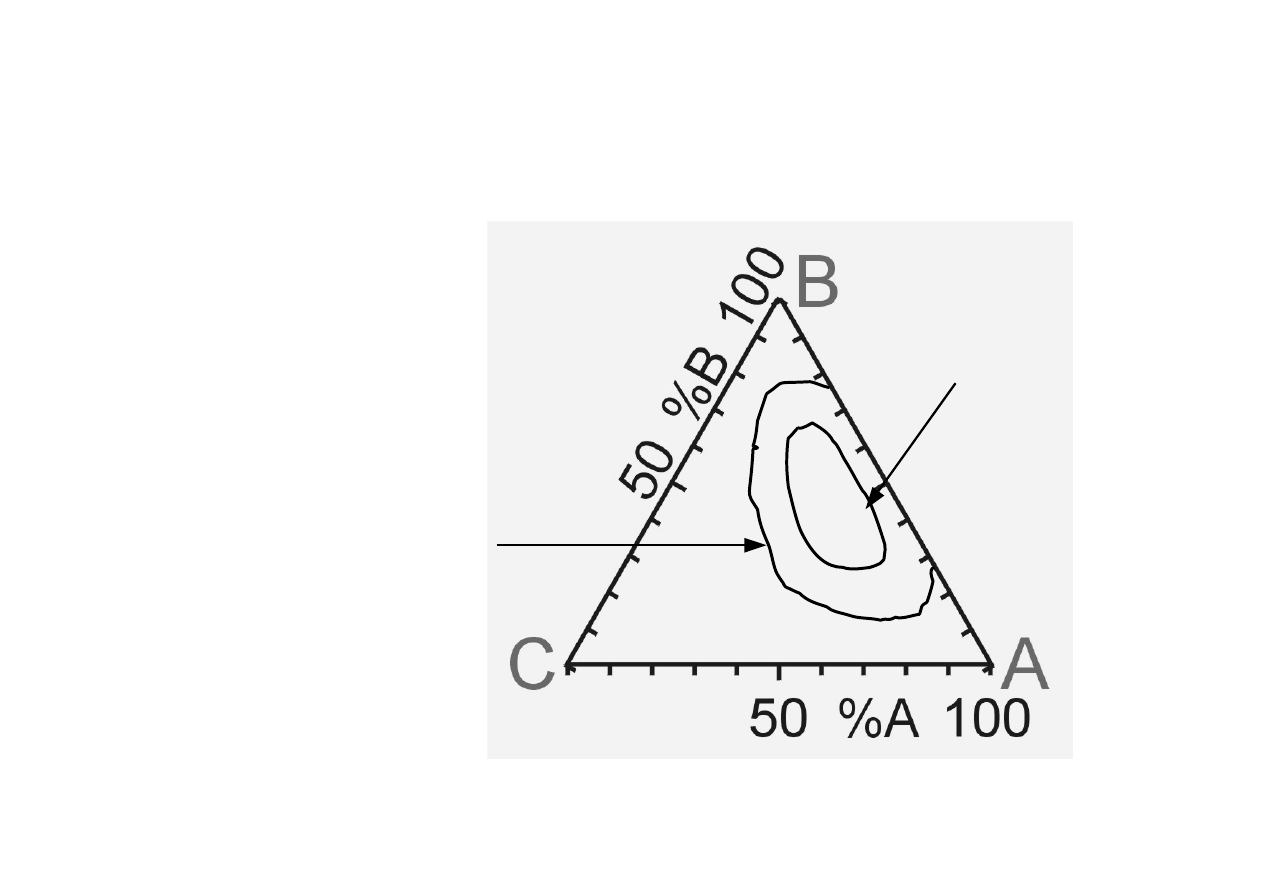
Chem. Fiz. TCH II/10

9

Układy trójskładnikowe (3).

A i B wykazują

ograniczoną wzajemną

rozpuszczalność

P=const, T=const

30

o

C

80

o

C

A = C

6

H

5

OH

B = H

2

O

C = (CH

3

)

2

CO

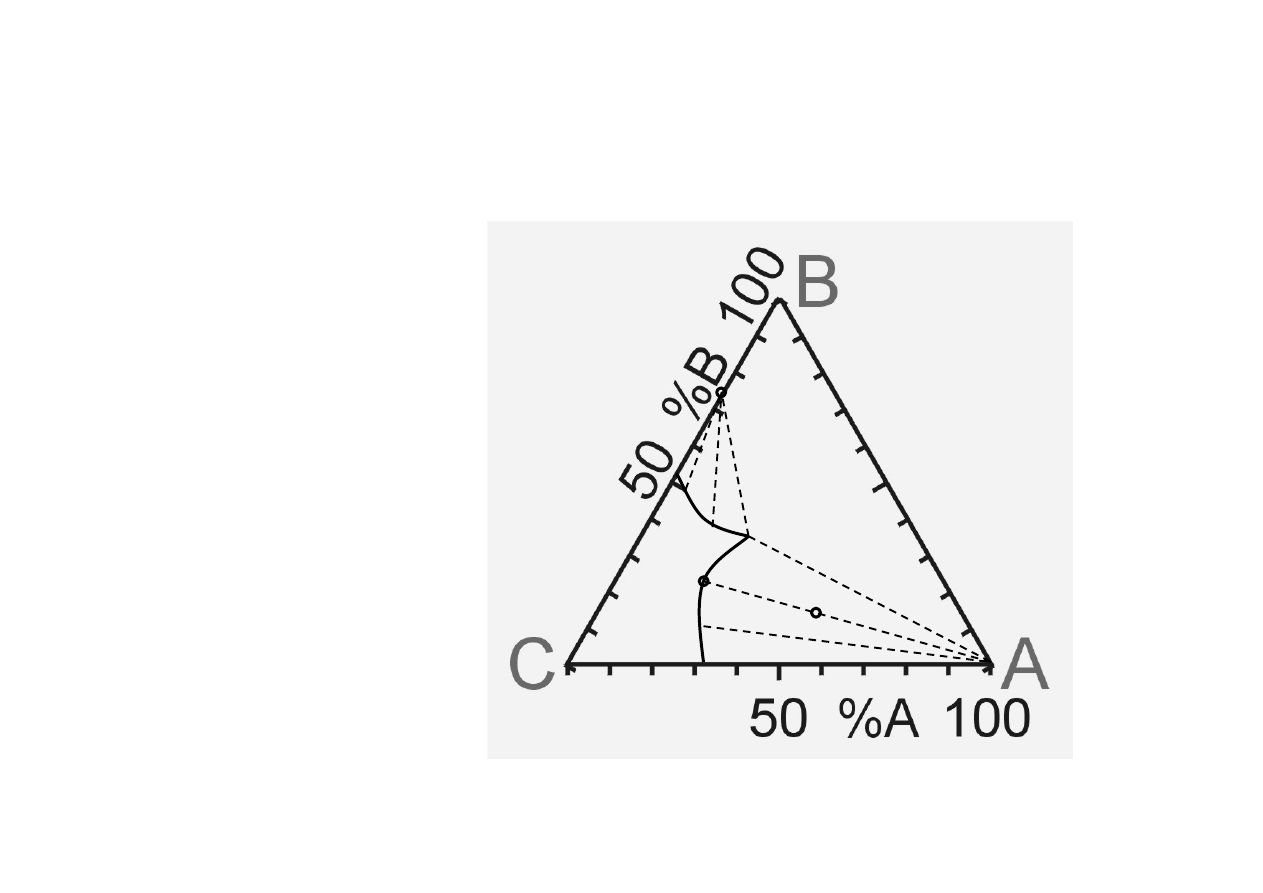
Chem. Fiz. TCH II/10

10

Układy trójskładnikowe (4).

P=const, T=const

A = sól1
B = sól2 (wspólny jon z A)
C = H

2

O

R

S

Z

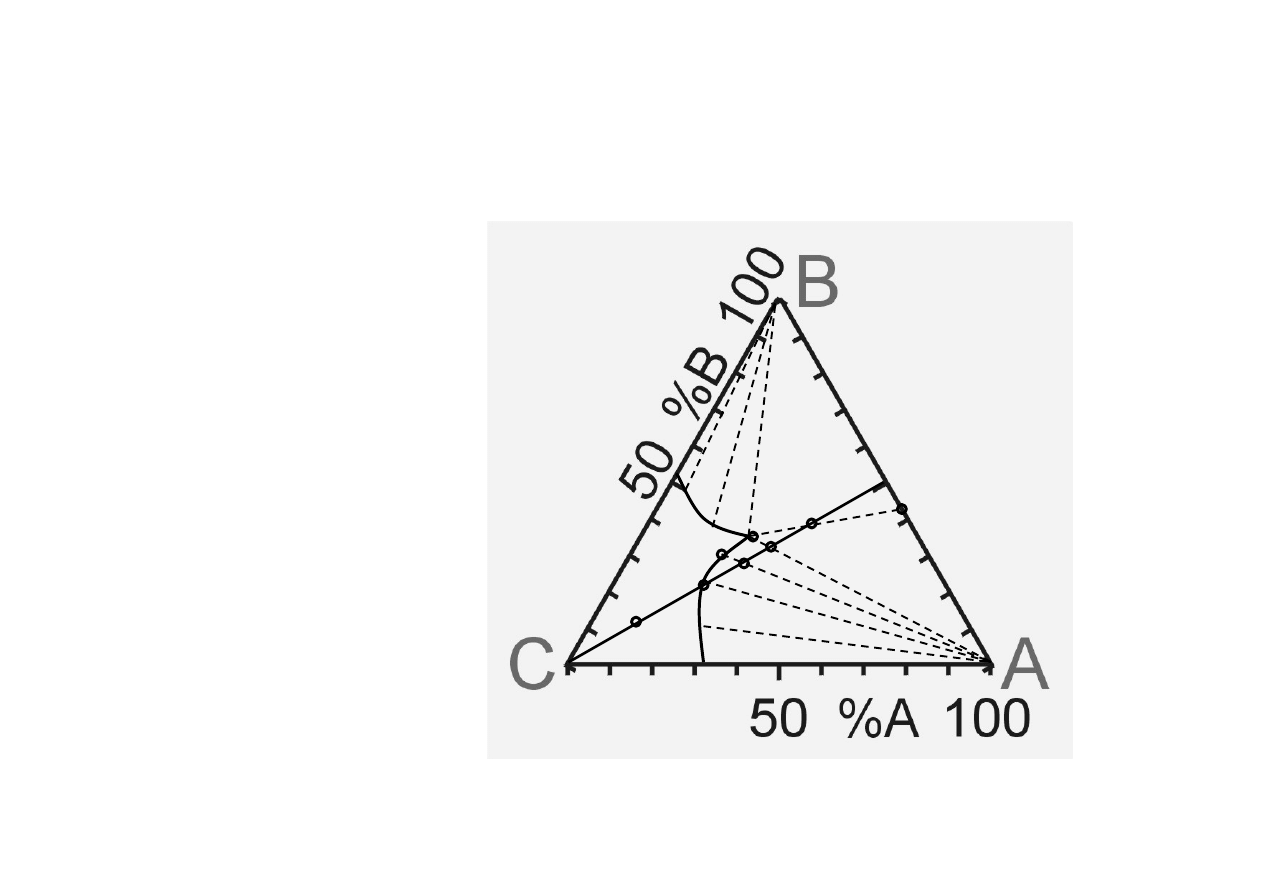
Chem. Fiz. TCH II/10

11

Układy trójskładnikowe (5).

P=const, T=const

A = sól1
B = sól2 (wspólny jon z A)
C = H

2

O

l

m

o

w

n

x y

z

Chem. Fiz. TCH II/10

12

Prawo podziału Nernsta

Dwa składniki (ciecze) o ograniczonej wzajemnej rozpuszczalności

a trzeci składnik (ciecz) obecny w bardzo niewielkich ilościach.

Stwierdzono empirycznie, że:

n

const

c

c

II

I

=

=

,

3

,

3

jeżeli P i T = const

Termodynamicznie:

II

I

,

3

,

3

µ

µ

=

zatem:

II

II

I

I

a

RT

a

RT

,

3

0

,

3

,

3

0

,

3

ln

ln

+

=

+

µ

µ

a także:

RT

a

a

I

II

II

I

0

,

3

0

,

3

,

3

,

3

ln

µ

µ

−

=

= const gdy T=const