1

Chem. Fiz. TCH II/06

1

Entalpia swobodna reakcji

chemicznej (1)

Dla reakcji: A = M (znane są liczne przypadki, choćby izomeryzacja)

Jeżeli dojdzie do infinitezymalnej zmiany składu mieszaniny reakcyj-

nej , czyli postępu reakcji, d

ξ

, tak że dn

A

= –d

ξ

, zaś dn

M

= d

ξ

, to:

dG =

µ

A

dn

A

+

µ

M

dn

M

= –

µ

A

d

ξ

+

µ

M

d

ξ

= (

µ

M

–

µ

A

)d

ξ

To entalpią swobodną reakcji

nazywamy pochodną:

A

M

T

P

r

G

G

µ

µ

ξ

−

=













∂

∂

=

∆

,

Na przykład, jeśli n

A,0

= 3, zaś postęp reakcji wyniósł

ξ=1,8, to n

A

=1,2, zaś

n

B

=1,8.

Postęp reakcji mierzymy po prostu w molach.
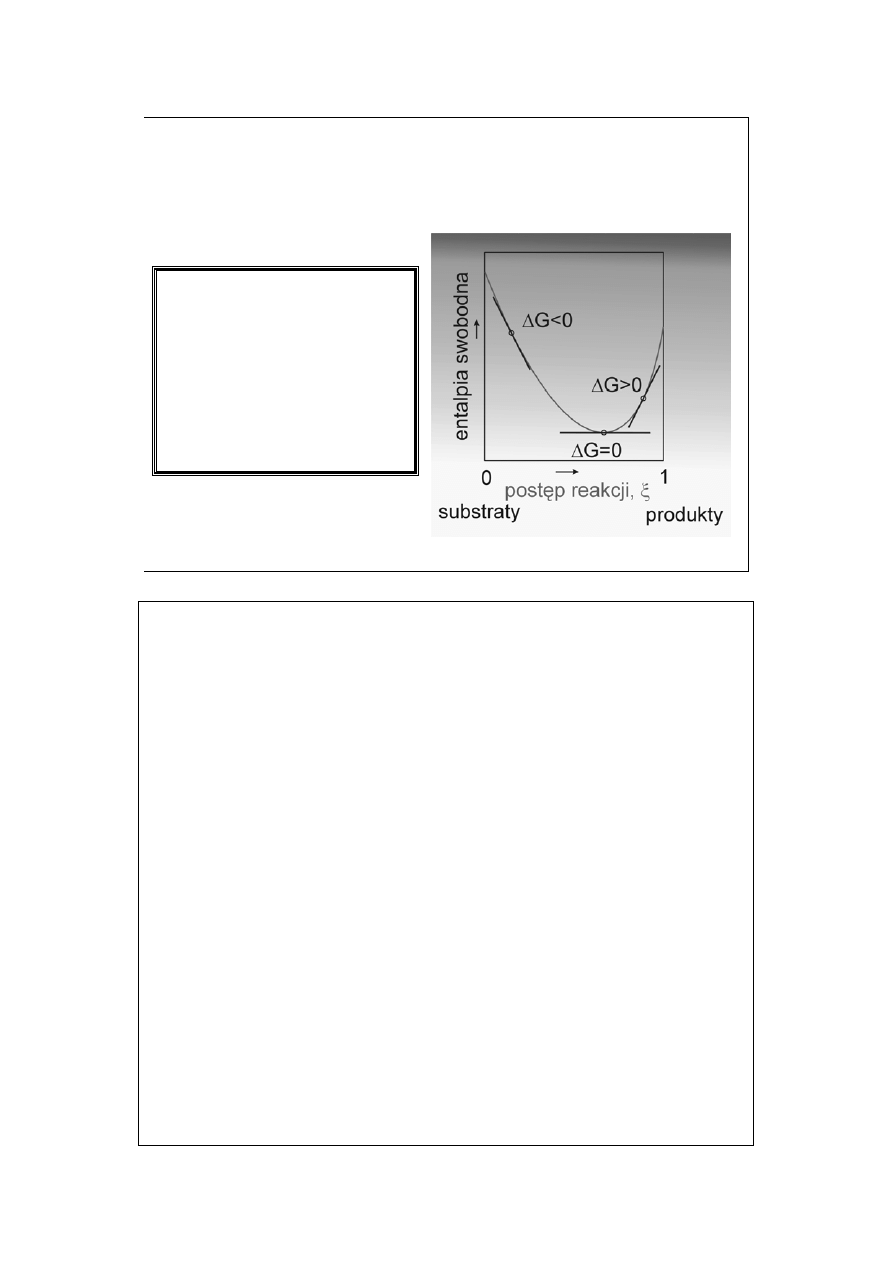
Tak zdefiniowana entalpia swobodna reakcji jest różnicą potencjałów
chemicznych produktów i substratów dla danego składu mieszaniny reakcyjnej.

2

Chem. Fiz. TCH II/06

2

Entalpia swobodna reakcji

chemicznej (2)

Zależnie od składu mieszani-
ny reakcyjnej możemy ocze-
kiwać samorzutnego przebie-
gu reakcji w prawo, w lewo
(samorzutnie przebiega reak-
cja przeciwna) lub pozosta-
wania przez nią w równowa-
dze.

3

Chem. Fiz. TCH II/06

3

Entalpia swobodna reakcji

chemicznej (3)

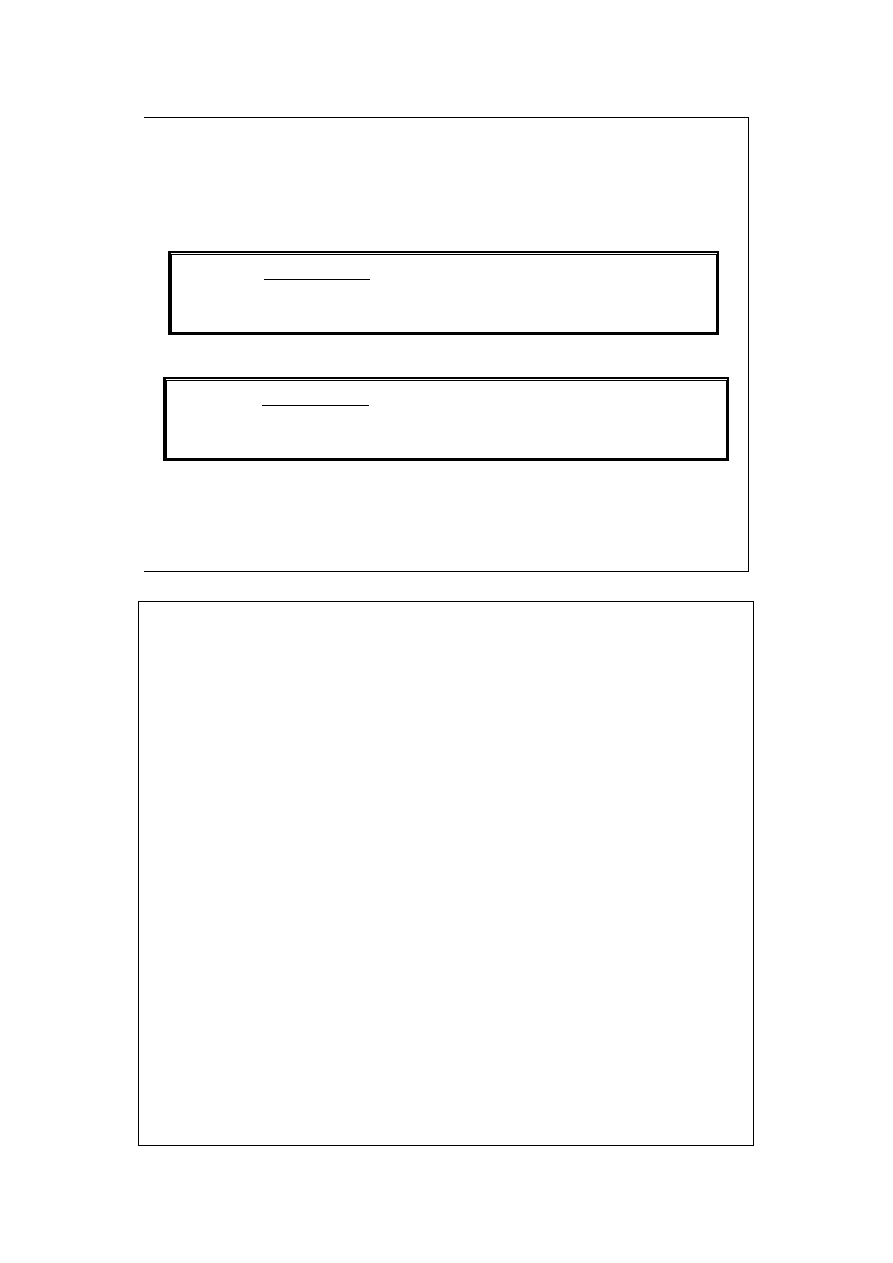
Reakcje egzoergiczne: wytwarzające pracę (mogące napędzać

inne procesy lub dostarczające pracy nie objętościowej), gdy

∆G<0. Np. reakcja w ogniwie galwanicznym.

Reakcje endoergiczne: zużywające pracę (wykorzystujące inne

procesy, potrzebujące pracy nie objętościowej), gdy ∆G>0. Np.

reakcja wymuszona w elektrolizerze.

4

Chem. Fiz. TCH II/06

4

Równowaga chemiczna (1)

Dla reakcji: A = M, gdy A i M są gazami doskonałymi,

gdzie Q jest jedną z możliwych (najprostszą ) postaci

ilorazu reakcji.

(

)

0

0

/

ln

P

P

RT

A

A

A

+

=

µ

µ

oraz

(

)

0

0

/

ln

P

P

RT

M

M

M

+

=

µ

µ

Q

RT

G

P

P

P

P

RT

G

r

A

M

A

M

A

M

r

ln

/

/

ln

0

0

0

0

0

+

∆

=

+

−

=

−

=

∆

µ

µ

µ

µ

0

,

0

,

0

A

tw

M

tw

r

G

G

G

∆

−

∆

=

∆

Pierwsze równanie pokazane i dyskutowane było na slajdach Entalpia swobodna
a lotność gazów (1) i Potencjał chemiczny mieszanin gazowych (1) wykładu nr 5.
Iloraz reakcji – patrz slajd Iloraz reakcji, wykład 4.
Wzór na ∆G

0

r

był już omawiany (w postaci ogólnej) na wykładzie 4, slajd

Entalpia swobodna (4).

5

Chem. Fiz. TCH II/06

5

Równowaga chemiczna (2)

0

ln

0

=

+

∆

r

r

Q

RT

G

W stanie równowagi, ∆G = 0, zatem

Równowagowy iloraz reakcji, Q

r

nazywamy stałą równowagi

reakcji i oznaczamy symbolem K . Jej definicja jest identyczna jak

ilorazu reakcji, lecz podstawione do wzoru ciśnienia (lotności,

stężenia, aktywności, itd.) nie są dowolne, lecz odpowiadają

składowi równowagowemu mieszaniny reakcyjnej.

P

r

K

RT

G

ln

0

−

=

∆

0

,

0

,

/

/

P

P

P

P

K

rów

A

rów

M

P

=

rów

A

rów

M

x

P

x

x

K

K

,

,

=

=

Stała jest tu zdefiniowana za pomocą ciśnień (prężności) równowagowych, stąd
dodajemy jej indeks P.
Gaz doskonały spełnia prawo Daltona, jeżeli więc w mieszaninie nie ma innych
składników poza A i M (np. rozcieńczającego je gazu, nie biorącego udział w
reakcji), to K

P

=K

x

.

6

Chem. Fiz. TCH II/06

6

Równowaga chemiczna (3)

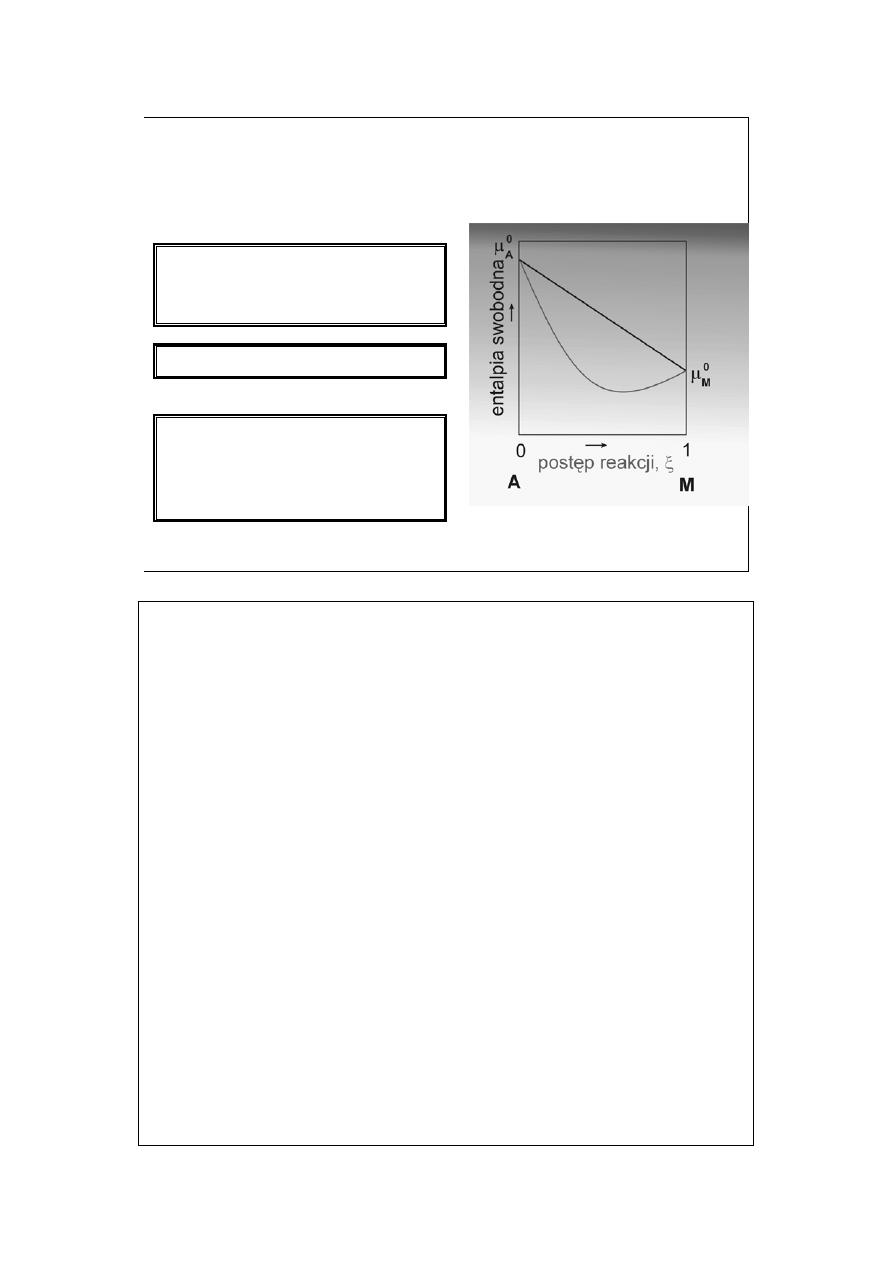
Dla gazu doskonałego zatem,

entalpia swobodna reakcji A = M

powinna zmieniać się liniowo:

jednak zmienia się inaczej:

Rzeczywisty przebieg

spowodowany jest wkładem

entalpii swobodnej mieszania

składników gazowych:

)

ln

ln

(

M

M

A

A

miesz

x

x

x

x

nRT

G

+

=

∆

7

Chem. Fiz. TCH II/06

7

Entalpia swobodna

mieszania (1)

{

}

{

}

)

/

ln(

)

/

ln(

0

0

0

0

P

P

RT

n

P

P

RT

n

n

n

G

M

M

A

A

M

M

A

A

p

+

+

+

=

+

=

µ

µ

µ

µ

stan początkowy: P

A

= P

M

= P

mieszanie

stan końcowy: P

A

+ P

M

= P

P

A

P

M

T = const.

{

}

{

}

)

/

ln(

)

/

ln(

0

0

0

0

P

P

RT

n

P

P

RT

n

G

M

M

M

A

A

A

k

+

+

+

=

µ

µ

)

ln

ln

(

)

/

ln(

)

/

ln(

M

M

A

A

M

M

A

A

p

k

miesz

x

x

x

x

nRT

P

P

RT

n

P

P

RT

n

G

G

G

+

=

+

=

−

=

∆

n = n

A

+ n

B

P

A

= x

A

P; P

M

= x

M

P

Gazy A i M nie reagują tutaj ze sobą.
Ostatnie przekształcenie wynika po prostu z prawa Daltona, patrz slajd Gaz
doskonały(2), wykład 5.
W powyższym przykładzie P

A

i P

B

maleją, mimo, że całkowite ciśnienie nie

ulega zmianie. Sprawdź, jak zmienia się entalpia swobodna, gdy mieszamy 2
jednakowe objętości gazu doskonałego o różnych ciśnieniach i połączymy oba
zbiorniki. Wtedy zmiana G jest sumą udziału pochodzącego od mieszania i od
zmiany ciśnień.
Przypominam, że entalpia swobodna zmienia się w każdym procesie, ale tylko w
izobarycznym możemy ją utożsamić z pracą nie objętościową.

8

Chem. Fiz. TCH II/06

8

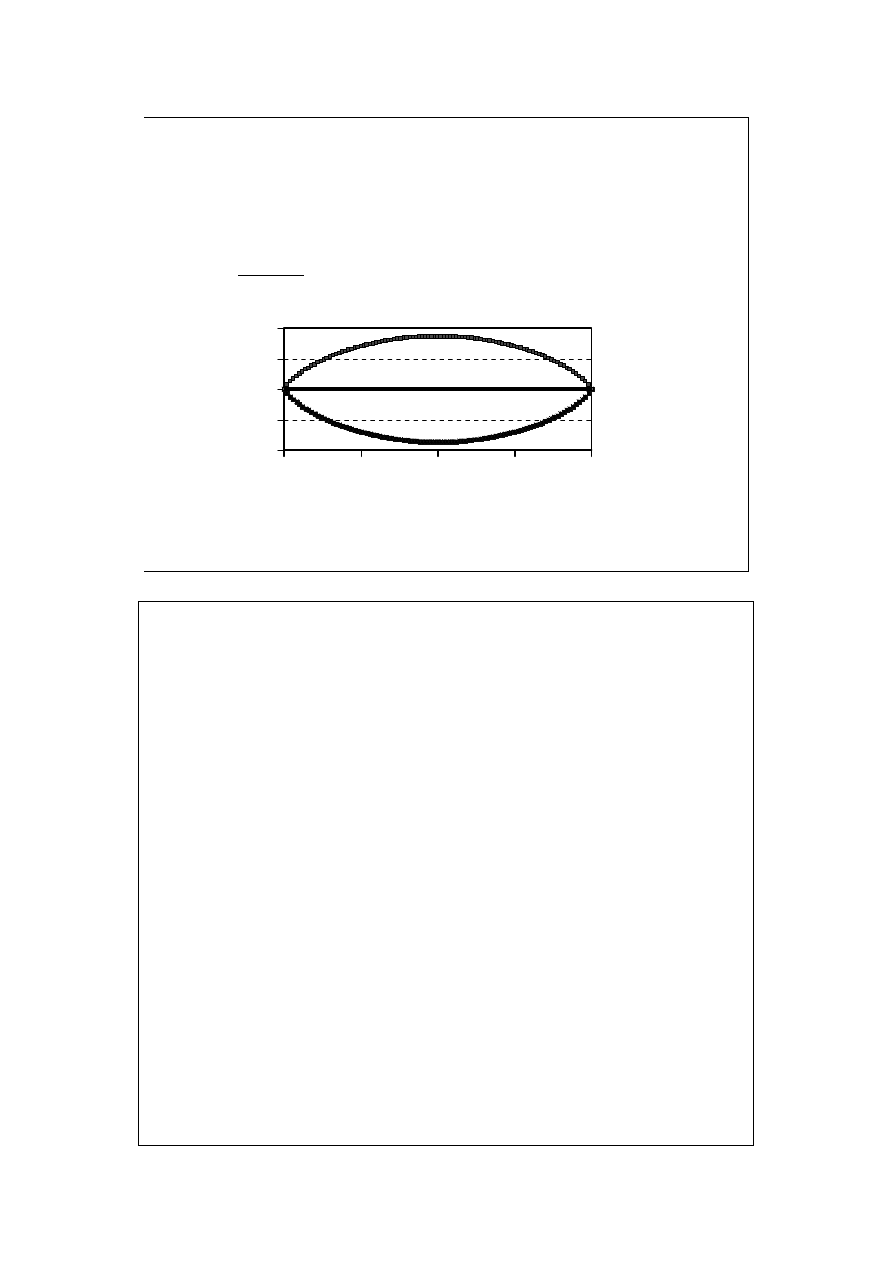
Entalpia swobodna

mieszania (2)

Te rm ody nam ic z ne funkc je m ie s z ania

-0,8

-0,4

0

0,4

0,8

0

0,25

0,5

0,75

1

ułamek molow y A, x

A

∆S

mie sz

/nR

∆G

mie sz

/nRT

∆H

mie sz

=

∆G

mie sz

+ T

∆S

mie s z

0

)

ln

ln

(

,

,

>

+

−

=

∆

=













∂

∆

∂

−

M

M

A

A

miesz

n

n

P

miesz

x

x

x

x

nR

S

T

G

M

A

Jak wynika ze wzoru,

∆

G

miesz

musi być ujemne, jako że ułamki molowe x<1.

Na podobnej zasadzie

∆

S

miesz

musi być dodatnie. Jeśli

∆

H

miesz

jest równe zeru, to

mieszanie jest procesem napędzanym wyłącznie entropowo. Zmiana entropii
układu wystarcza, ponieważ ciepło z otoczeniem wymieniane nie jest.

9

Chem. Fiz. TCH II/06

9

Równowaga chemiczna (4)

;

;

;

;

ξ

ν

ξ

ν

ξ

ν

ξ

ν

d

dn

d

dn

d

dn

d

dn

N

N

M

M

B

B

A

A

=

=

−

=

−

=

Przypadek ogólny. Dla reakcji:

ν

A

A +

ν

B

B + ... =

ν

M

M +

ν

N

N + ...

lub ogólnie:

ξ

ν

d

dn

Y

Y

±

=

wtedy:

ξ

ν

µ

µ

d

dn

dG

Y

Y

Y

Y

Y

Y













=

=

∑

∑

zaś:

∑

=













∂

∂

=

∆

Y

Y

Y

T

P

r

G

G

ν

µ

ξ

,

podstawiając:

Y

Y

Y

a

RT ln

0

+

=

µ

µ

otrzymamy:

Q

RT

G

G

r

r

ln

0

+

∆

=

∆

gdzie:

∑

∆

=

∆

Y

Y

tw

Y

r

G

G

0

,

0

ν

oraz:

∏

=

Y

Y

Y

a

Q

ν

Uwaga: współczynniki

ν

Y

dla substratów są ujemne.

10

Chem. Fiz. TCH II/06

10

Równowaga chemiczna (5)

Przypadek ogólny. Dla reakcji:

ν

A

A +

ν

B

B + ... =

ν

M

M +

ν

N

N + ...

zauważmy, że (uwzględniając znaki

ν

Y

):

0

,

0

,

0

,

0

,

0

,

0

B

tw

B

A

tw

A

N

tw

N

M

tw

M

Y

Y

tw

Y

r

G

G

G

G

G

G

∆

−

∆

−

∆

+

∆

=

∆

=

∆

∑

ν

ν

ν

ν

ν

zaś druga część równania:

∑

+

∆

=

∆

Y

Y

Y

r

r

a

RT

G

G

ln

0

ν

∑

∑

∑

∏

=

=

=

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

Y

a

RT

a

RT

a

RT

a

RT

ν

ν

ν

ν

ln

ln

ln

ln

ponownie, uwzględniając znaki

ν

Y

:

Q

a

a

a

a

a

a

a

a

a

B

A

N

M

B

A

N

M

Y

B

A

N

M

B

A

N

M

Y

Y

=

=

=

−

−

∏

ν

ν

ν

ν

ν

ν

ν

ν

ν

Rozwinięcie pierwszej części równania jest identyczne z równaniem podawanym
na wykładzie 4, slajd Entalpia swobodna (4).
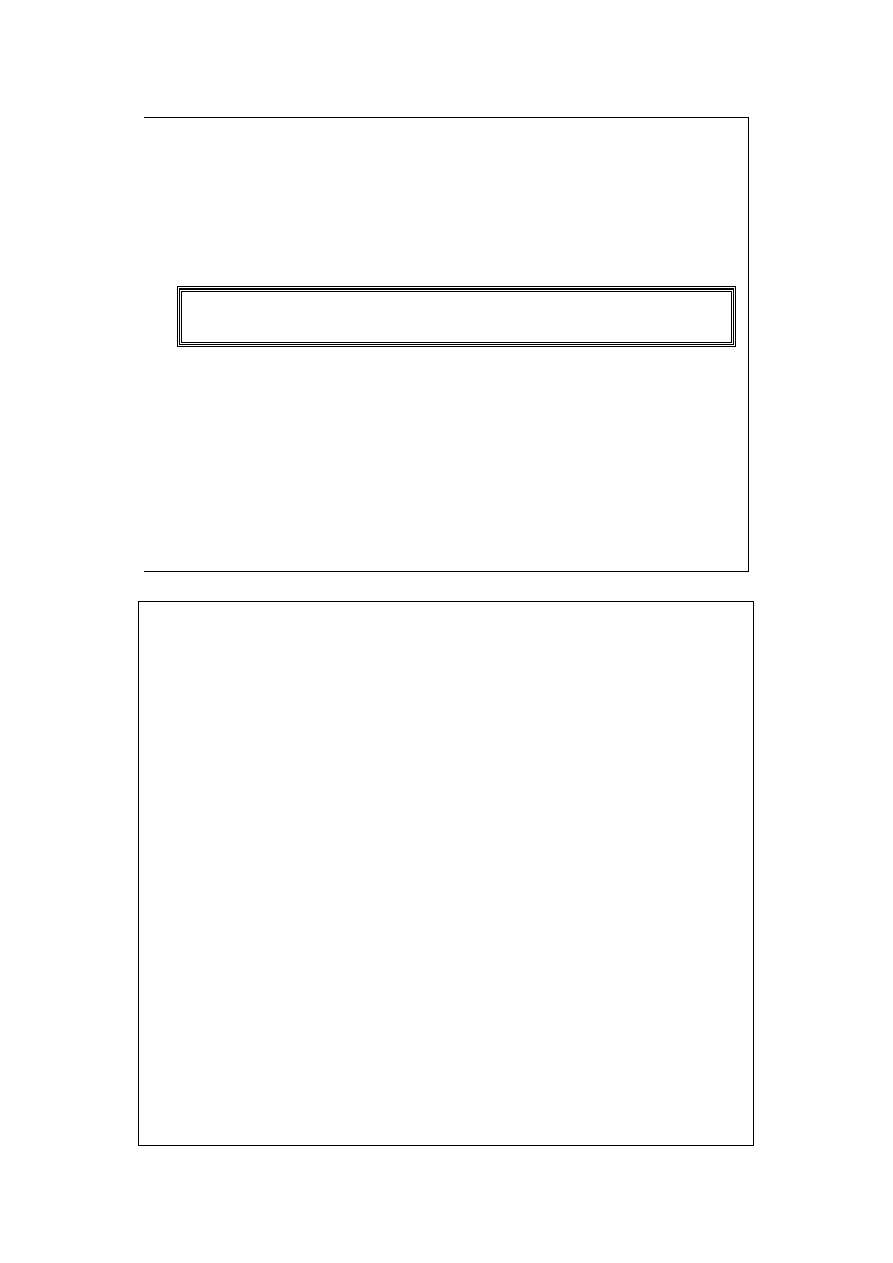
Uwaga:

Wielokrotność a logarytmu z X jest logarytmem z X

podniesionego do potęgi a (X

a

).

Suma logarytmów jest logarytmem z iloczynu

składników.

11

Chem. Fiz. TCH II/06

11

Równowaga chemiczna (6)

W stanie równowagi:

0

=

∆

r

G

0

ln

0

=

+

∆

K

RT

G

r

K

RT

G

r

ln

0

−

=

∆

(

)

R

S

RT

H

RT

S

T

H

RT

G

r

r

r

r

R

r

e

e

e

e

K

/

/

/

/

0

0

0

0

∆

∆

−

∆

−

∆

−

∆

−

=

=

=

Do ostatniego równania można także dojść

wychodząc z rozkładu Boltzmanna

12

Chem. Fiz. TCH II/06

12

Prawo działania mas

Dla reakcji:

ν

A

A +

ν

B

B + ... =

ν

M

M +

ν

N

N + ...

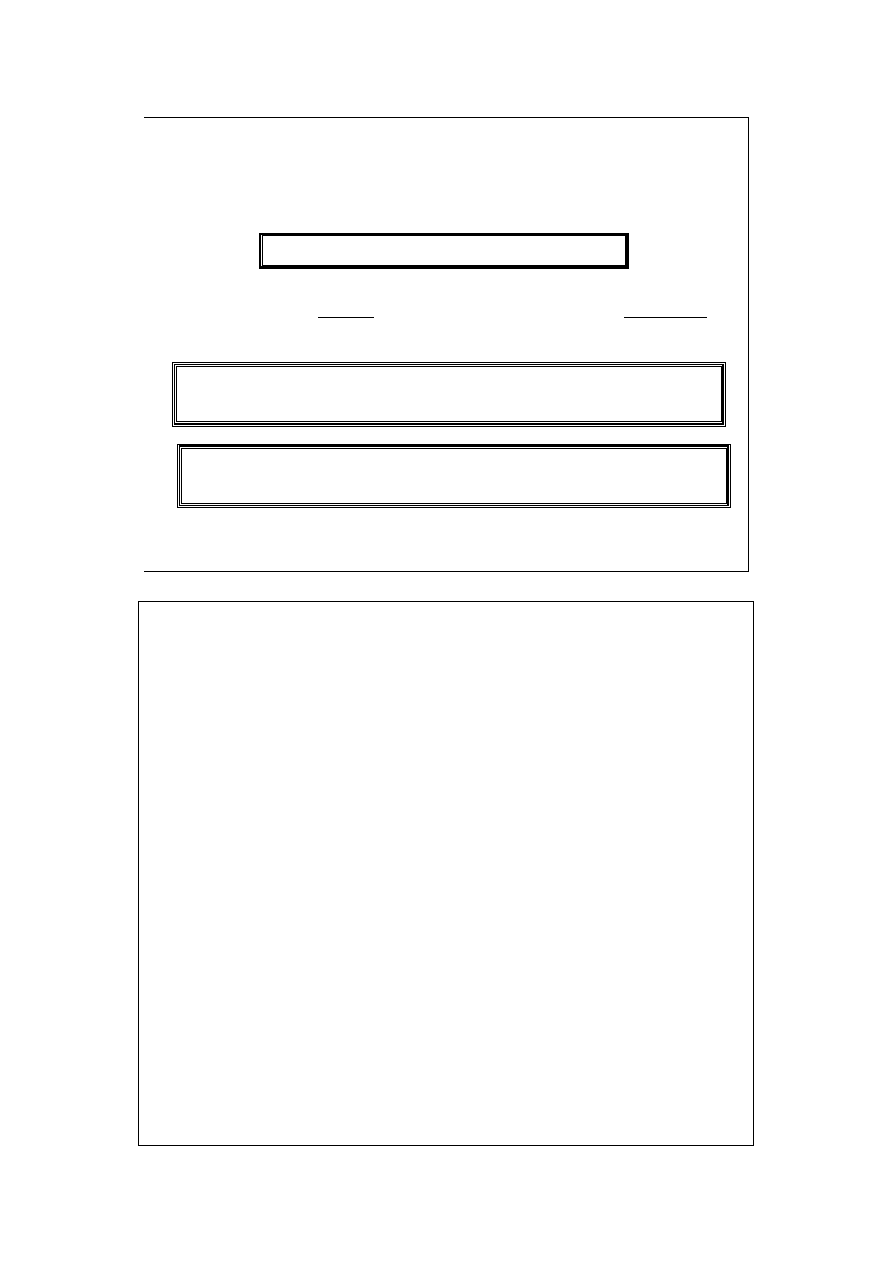
pozostającej w stanie równowagi, wielkość K, zwana

termodynamiczną stałą równowagi tej reakcji

jest wielkością charakterystyczną dla reakcji i stałą w danej

temperaturze.

B

A

N

M

Y

rówB

rówA

rówN

rówM

Y

rówY

rów

a

a

a

a

a

Q

K

ν

ν

ν

ν

ν

=

=

=

∏

(znane też jako prawo Guldberga – Waagego)

13

Chem. Fiz. TCH II/06

13

Równowaga chemiczna (7)

Co oznacza symbol a we wzorach:

B

A

N

M

Y

B

A

N

M

Y

Y

a

a

a

a

a

Q

ν

ν

ν

ν

ν

=

=

∏

B

A

N

M

Y

rówB

rówA

rówN

rówM

Y

rówY

rów

a

a

a

a

a

Q

K

ν

ν

ν

ν

ν

=

=

=

∏

Nadal bez formalnego jej definiowania, wielkość tę nazwiemy

aktywnością

Właściwie wszędzie powinno być a

Y

/a

0

Y

, aby iloraz reakcji i stała

równowagi były wielkościami bezwymiarowymi!

Raz jeszcze podkreślam różnicę między Q a Q

r

, czyli K.

14

Chem. Fiz. TCH II/06

14

Równowaga chemiczna (8)

Co powinniśmy wiedzieć o aktywnościach:

¾ aktywność jest „skorygowanym stężeniem” podobnie jak lotność

„skorygowanym ciśnieniem” (wyrażana w jednostkach stężenia);

¾ a

0

oznacza aktywność standardową (w stanie standardowym);

¾ aktywność standardowa (niezależnie od sposobu definiowania

stanu standardowego) wynosi 1;

¾ stanem standardowym czystych ciał stałych i cieczy jest ich ter-

modynamicznie trwała postać w danej temperaturze pod ciśnie-
niem standardowym.

15

Chem. Fiz. TCH II/06

15

Równowaga chemiczna (9)

Co powinniśmy wiedzieć o aktywnościach (c.d.):

¾ dla cieczy: a

Y

=

γ

Y

x

Y

, gdzie

γ

Y

jest współczynnikiem aktywności

reagenta Y;

¾ dla gazów za a/a

0

podstawiamy f/P

0

i także mamy do czynienia

z termodynamiczną stałą równowagi;

¾ dla gazu doskonałego za a/a

0

podstawiamy P/P

0

.

Współczynniki aktywności można różnie definiować; x

Y

oznacza ułamek

molowy.

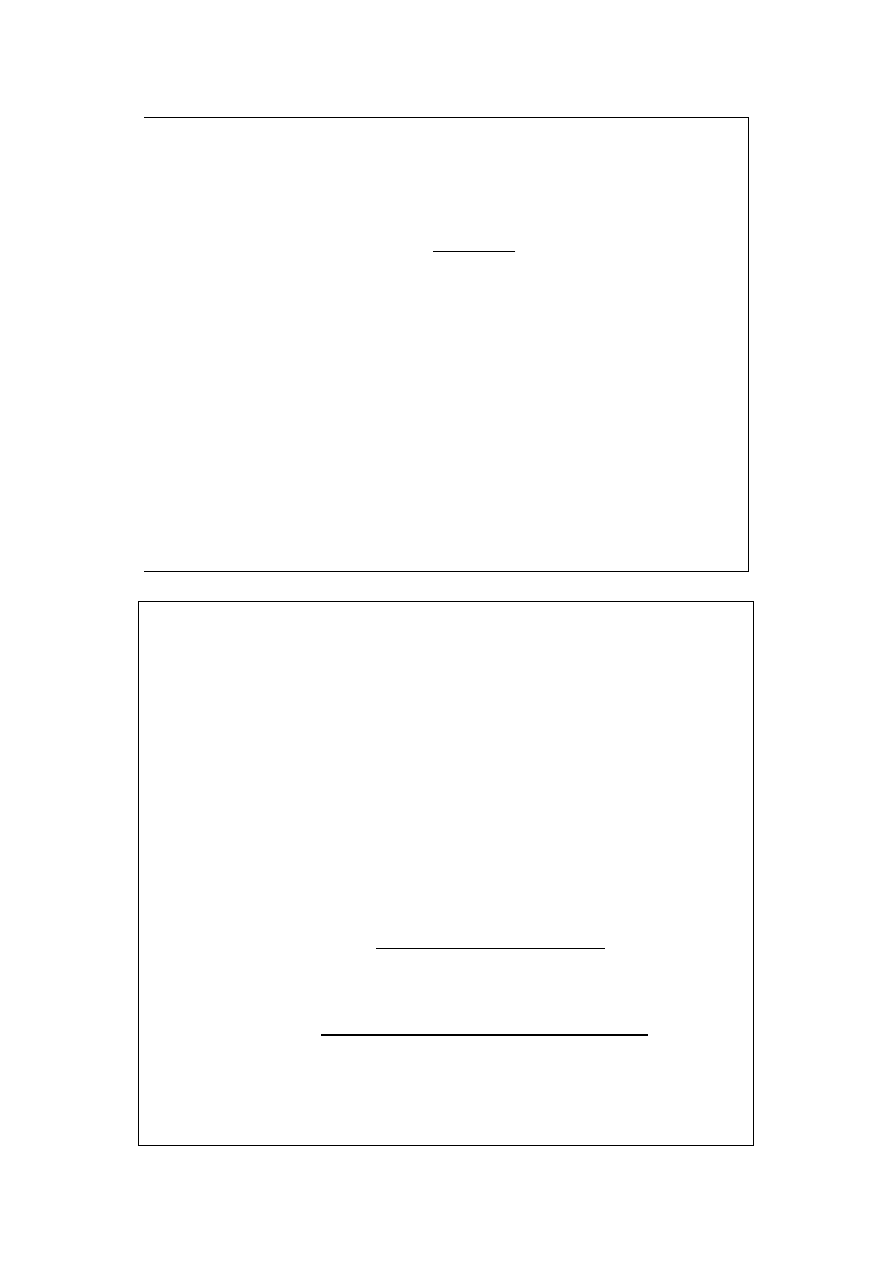
16

Chem. Fiz. TCH II/06

16

Wnioski z prawa

działania mas

.

const

a

a

a

a

a

K

B

A

N

M

Y

rówB

rówA

rówN

rówM

Y

rówY

=

=

=

∏

ν

ν

ν

ν

ν

™ Jeżeli zwiększymy aktywności (stężenia, lotności, ciśnienia ...)

substratów reakcji znajdującej się w równowadze, ta zacznie prze-

biegać w prawo, aby zmniejszyć licznik, zwiększyć mianownik

i zachować stałość K;

™ Jeżeli zwiększymy aktywności produktów reakcji znajdującej się

w równowadze, to przechylimy równowagę reakcji w lewo;

™ Jeżeli zmniejszymy aktywności substratów ...

™ Jeżeli zmniejszymy aktywności produktów ...

Wymienione wnioski wskazują co się
stanie, jeśli reakcję pozostającą w
równowadze „wybijemy” z tego stanu,
bowiem w danej temperaturze stałość K
musi być zachowana. Zajmiemy się
teraz wpływem parametrów przebiegu
reakcji, tzn. ogólnego ciśnienia i
temperatury na stan równowagi (skład
równowagowy). Przypominam, że stała
równowagi nie zależy od ciśnienia, choć
zależy od temperatury.

17

Chem. Fiz. TCH II/06

17

Reguła przekory

Le Chateliera (1)

Jeżeli układ w którym zachodzi reakcja chemiczna pozostającą

w stanie równowagi zostaje poddany działaniu czynnika

zaburzającego (P, T), to zachodzą w nim takie zmiany, jakie mogą

zminimalizować działanie tego czynnika.

Temperatura:

podwyższenie temperatury cofa (przesuwa w lewo)

równowagę reakcji egzotermicznych, zaś w prawo – reakcji

endotermicznych.

Ciśnienie:

wywiera wpływ jedynie na stan równowagi reakcji,

w których zmienia się liczba moli reagentów gazowych.

Do wniosków wypływających z reguły przekory można też dojść na drodze
ścisłej analizy prawa działania mas. Jednak jest ona cenną (i bezbłędną)
wskazówką jakościową dla przewidywania wpływu ciśnienia i temperatury, a
także doskonałym narzędziem jakościowej weryfikacji poprawności wyników
obliczonych na drodze ścisłej, które nie mogą prowadzić do wniosków
sprzecznych z tą regułą.
Katalizatory nie wywierają wpływu na stałą równowagi, a jedynie na szybkość
dochodzenia do stanu równowagi !!!

18

Chem. Fiz. TCH II/06

18

Reguła przekory

Le Chateliera (2)

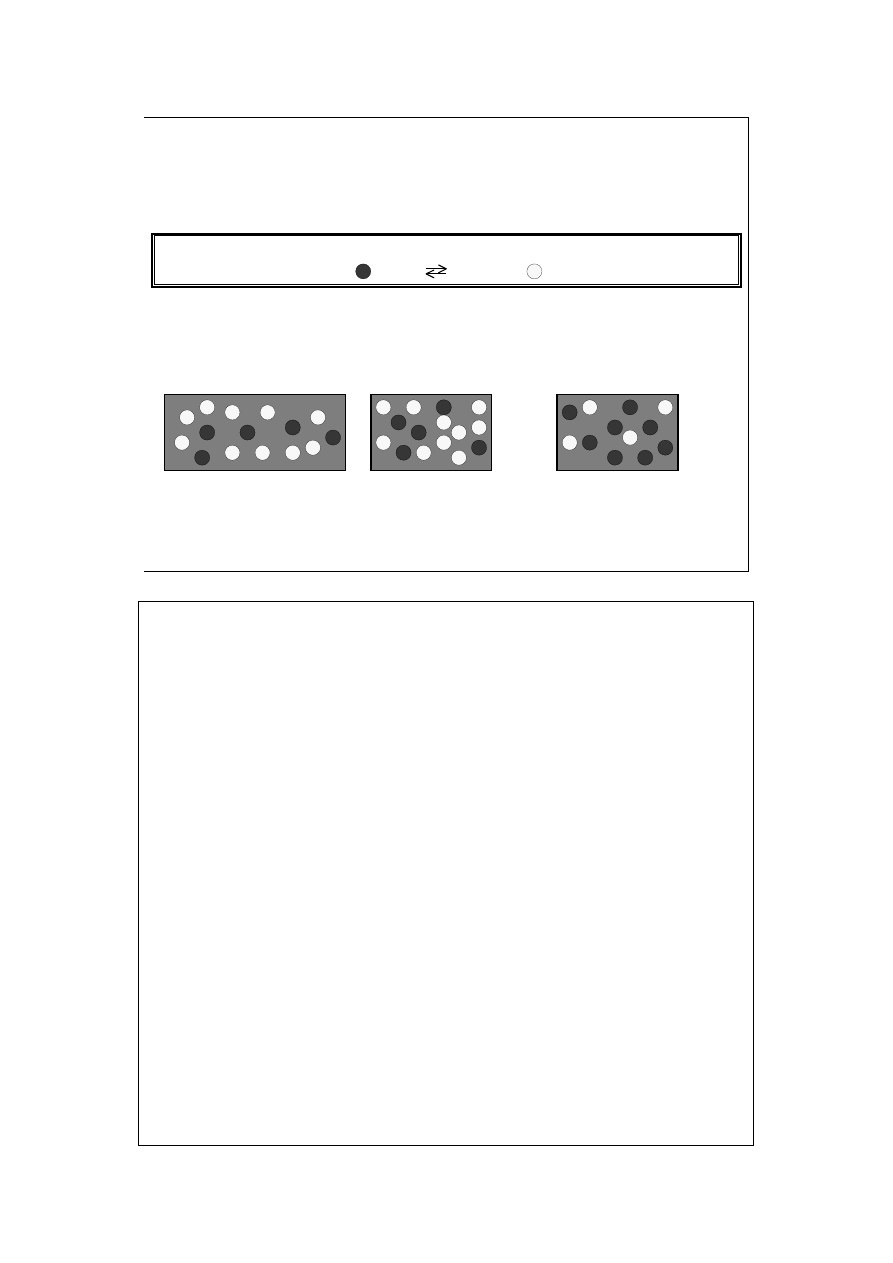
Reguła powiada: w reakcjach przebiegających ze zwiększeniem liczby

moli reagentów gazowych, wzrost ciśnienia prowadzi do przesunięcia

stanu równowagi w lewo, jego obniżenie zaś – w prawo.

Wpływ ciśnienia na reakcję dysocjacji:

A 2B

stan początkowy, P

p

zaburzenie, P

2

>P

p

odpowiedź układu,

P

2

>P

k

>P

p

Cząsteczek A powstało 2 razy mniej niż znikło cząsteczek B. W sumie liczba
cząsteczek zmalała, zatem ciśnienie także zmalało. Stan równowagi został
jednak przesunięty w lewo. Nowa równowaga faworyzuje substraty w stosunku
do poprzedniej.

19

Chem. Fiz. TCH II/06

19

Wpływ ciśnienia na

dysocjację w fazie gaz. (1)

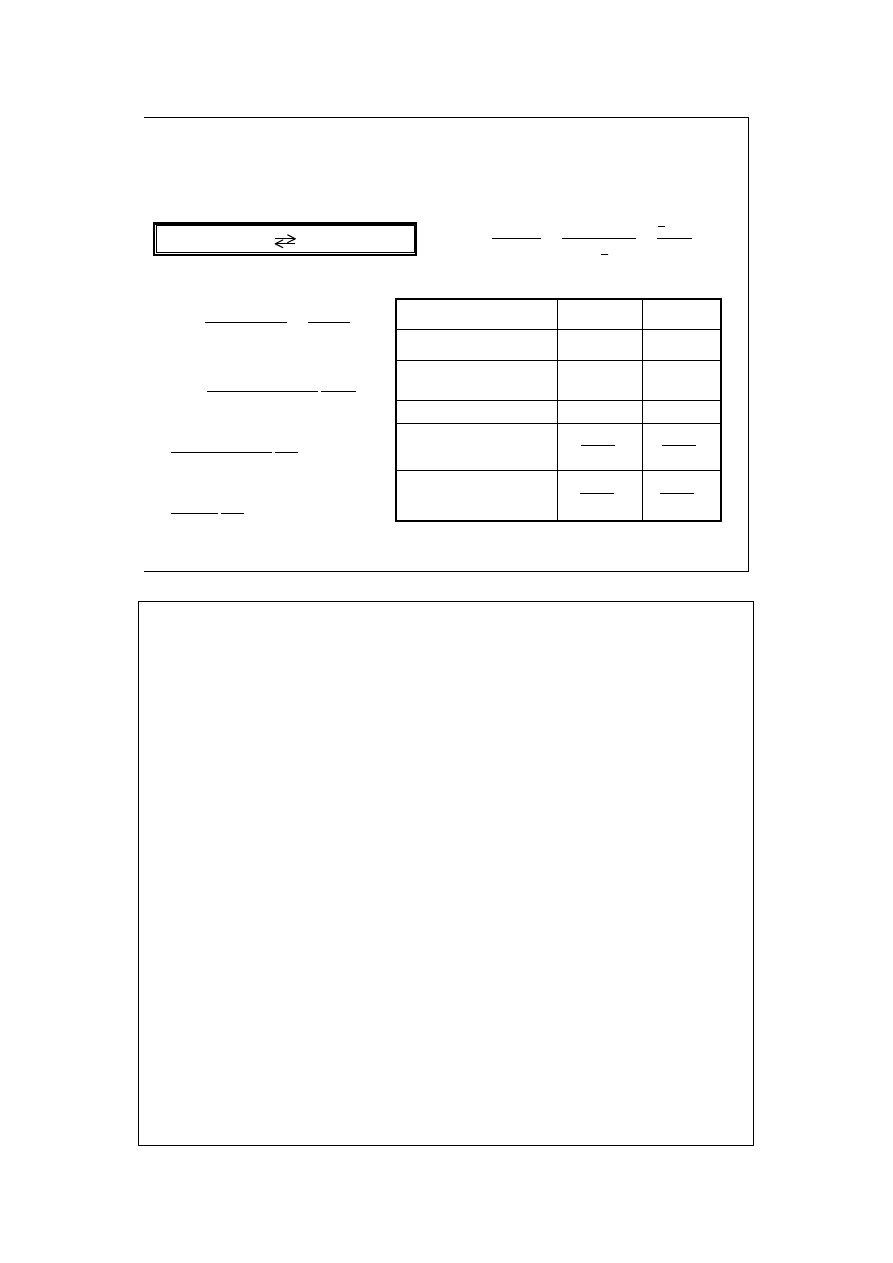
Załóżmy, że A i M są gazami doskonałymi. Wtedy:

A 2M

n

n

n

n

n

n

n

n

n

M

M

A

A

A

2

1

2

1

=

+

−

=

−

=

α

ciśnienie cząstkowe

ułamek molowy, x

w stanie równowagi

zmiana do stanu

równowagi

początkowo

2nα

n(1–α)

+2αn

–αn

0

n

M

A

0

2

0

2

0

/

)

/

(

P

P

P

P

P

P

P

K

A

M

A

M

=

=

α

α

+

−

1

1

α

α

+

1

2

P

α

α

+

−

1

1

P

α

α

+

1

2

(

)

(

) (

)

(

)(

)

0

2

2

0

2

0

2

2

2

1

4

1

1

4

1

1

1

4

P

P

P

P

PP

P

K

α

α

α

α

α

α

α

α

α

−

=

−

+

=

−

+

+

=

20

Chem. Fiz. TCH II/06

20

Wpływ ciśnienia na

dysocjację w fazie gaz. (2)

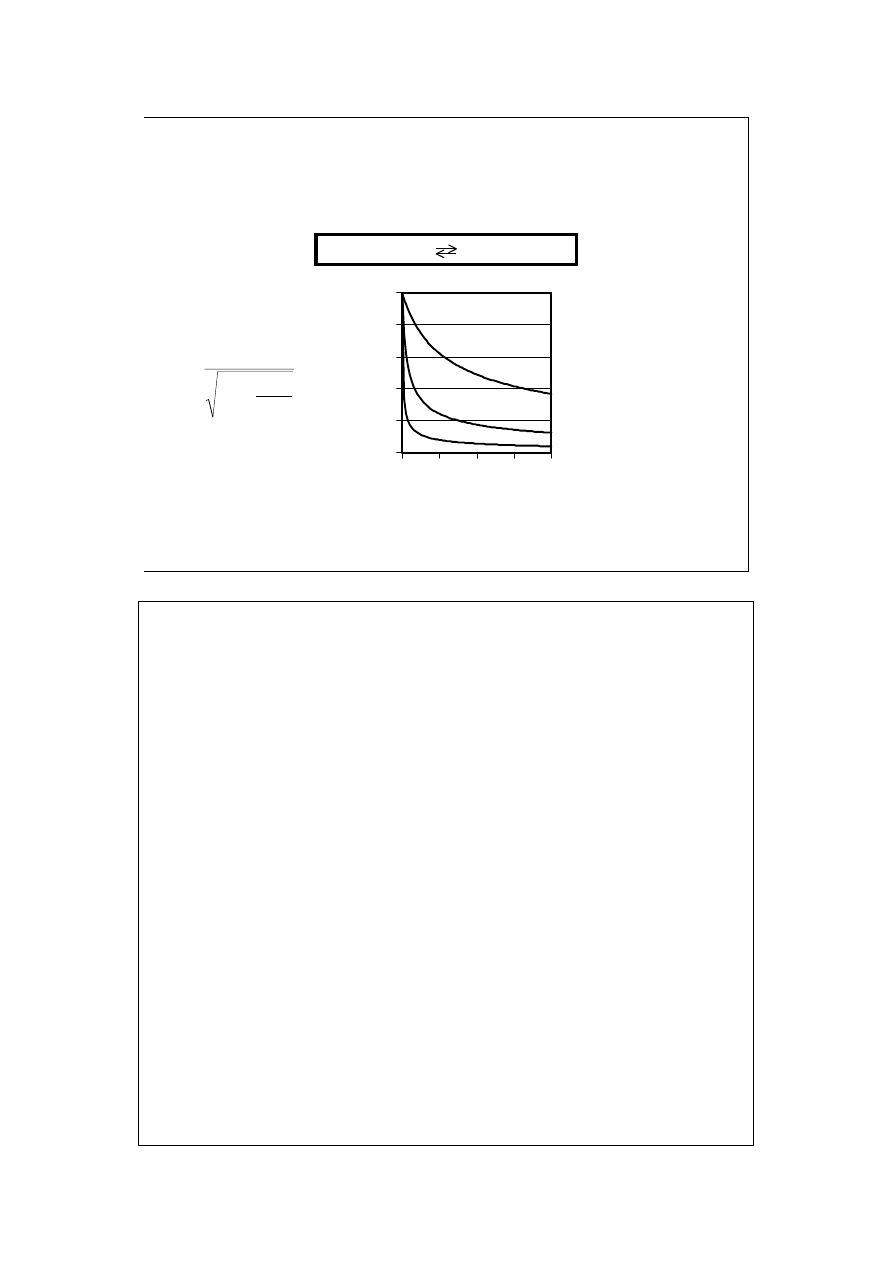
A 2M

0

4

1

1

KP

P

+

=

α

0

0,2

0,4

0,6

0,8

1

0

4

8

12

16

P/P

0

st

o

p

ie

ń

d

y

s

o

c

ja

c

ji

,

α

K=10

K=1

K=0,1

czyste M

czyste A

Im większe K, tym większy stopień dysocjacji. Im większe P, tym mniejszy
stopień dysocjacji.

21

Chem. Fiz. TCH II/06

21

Zależność entalpii

swobodnej od temperatury

Równanie Gibbsa – Helmholtza:

S

T

G

P

−

=













∂

∂

T

H

G

T

G

P

−

=













∂

∂

T

H

T

G

T

G

P

−

=

−













∂

∂













−













∂

∂

=

−













∂

∂

=

+













∂

∂

=

























∂

∂

T

G

T

G

T

T

G

T

G

T

T

dT

d

G

T

G

T

T

G

T

P

P

P

P

1

1

1

1

2

2

1

T

H

T

G

T

H

G

T

T

G

T

P

−

=













−

−

=

























∂

∂

2

T

H

T

G

T

P

−

=

























∂

∂

Równanie G – H (ułatwia zapamiętanie).

22

Chem. Fiz. TCH II/06

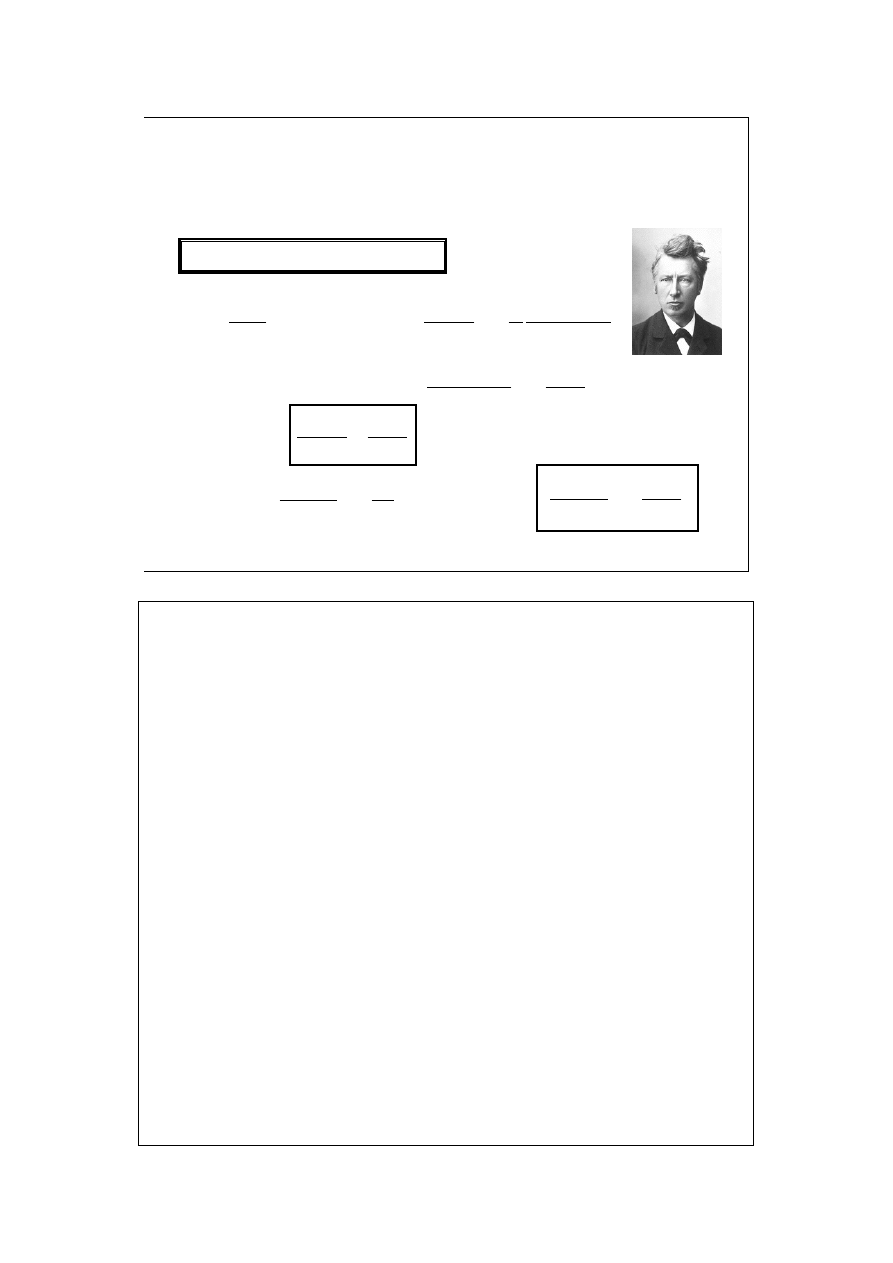
22

Wpływ temperatury na

stałą równowagi (1)

Równanie van’t Hoffa:

Jacobus

Henricus

van’t Hoff

RT

G

K

r

0

ln

∆

−

=

(

)

dT

T

G

d

R

dT

K

d

r

/

1

ln

0

∆

−

=

różniczkując

względem T

otrzymujemy:

a używając równania G – H:

(

)

2

0

0

/

T

H

dT

T

G

d

r

r

∆

−

=

∆

otrzymujemy:

2

0

ln

RT

H

dT

K

d

r

∆

=

a ponieważ:

otrzymujemy

równoważnie:

2

1

)

/

1

(

T

dT

T

d

−

=

R

H

T

d

K

d

r

0

)

/

1

(

ln

∆

−

=

Van’t Hoff otrzymał jako pierwszy nagrodę Nobla z chemii w 1901.
Różniczkując pierwsze równanie względem T używamy zwykłych pochodnych,
tak

∆

G

0

r

jak i K zależą tylko od temperatury, a nie zależą od ciśnienia.

23

Chem. Fiz. TCH II/06

23

Wpływ temperatury na

stałą równowagi (2)

Równanie van’t Hoffa

(scałkowane):

2

0

ln

RT

H

dT

K

d

r

∆

=

dT

RT

H

K

d

r
2

0

ln

∆

=

∫

∫

∆

=

2

1

2

1

2

0

ln

T

T

r

T

T

dT

RT

H

K

d













−

∆

−

=

∆

=

=

−

∫

2

1

2

2

0

2

0

1

2

1

2

1

1

1

ln

ln

ln

2

1

T

T

R

H

dT

T

R

H

K

K

K

K

r

T

T

r

Identyczne wyrażenie otrzymamy wychodząc z drugiej

postaci równania van’t Hoffa

24

Chem. Fiz. TCH II/06

24

Zależności pomiędzy

stałymi równowagi (1)

Stałymi równowagi w pełnym znaczeniu są jedynie termodynamiczne

stałe równowagi, zdefiniowane jako:

oznacza

gdzie

;

0

a

a

a

a

K

Y

rówY

Y

∏

=

ν

oznacza

gdzie

;

0

P

f

f

f

K

Y

rówY

Y

∏

=

ν

Stosowane także i często nazywane stałymi równowagi wyrażenia:

oznacza

gdzie

;

0

c

c

c

c

K

Y

rówY

c

Y

∏

=

ν

oznacza

gdzie

;

0

P

P

P

P

K

Y

rówY

P

Y

∏

=

ν

Są jedynie przybliżeniami (poza K

P

dla gazu doskonałego samemu

jednak będącego tylko przybliżonym modelem) i raczej powinny być

nazywane równowagowymi ilorazami stężeń, ciśnień, itp.)

25

Chem. Fiz. TCH II/06

25

Zależności pomiędzy

stałymi równowagi (2)

Uwzględniając a

Y

=

γ

Y

x

Y

(stężenia wyraźmy jako ułamki molowe):

(

)

(

) (

)

∏

∏

∏

=

=

=

Y

x

rówY

Y

rówY

Y

rówY

rówY

K

K

x

x

K

Y

Y

Y

Y

γ

ν

ν

ν

ν

γ

γ

gdzie K

x

i K

γ

są odpowiednimi ilorazami równowagowymi.

Dla substancji gazowych zapisać można:

(

)

(

) ( )

∏

∏

∏

=

=

=

Y

P

rówY

Y

rówY

Y

rówY

rówY

K

K

P

P

K

Y

Y

Y

Y

φ

ν

ν

ν

ν

φ

φ

a także:

0

lim

→

=

P

P

K

K

co oznacza:

1

lim

0

=

→

P

K

φ

Symbolem

φ

oznaczamy współczynnik lotności, patrz slajd Entalpia swobodna a

lotność gazów (2) w wykładzie 5.
Zakładanie że K

φ

, a zwłaszcza K

γ

=1 jest uproszczeniem i nie odzwierciedla

dokładnie termodynamiki danej reakcji.

26

Chem. Fiz. TCH II/06

26

Zależności pomiędzy

stałymi równowagi (3)

Dla reakcji w fazie gazowej istnieją dalsze możliwości wyrażania K

P

:

ν

∆













⋅

=

0

P

RT

K

K

c

P

bowiem:

cRT

V

nRT

P

=

=

gdzie c jest w

mol/m

3

3

0

0

mol/m

0224

,

0

1

1 ≅

=

m

V

c

B

A

N

M

Y

Y

ν

ν

ν

ν

ν

ν

−

−

+

=

=

∆

∑

∆

ν

dotyczy wyłącznie reagentów gazowych

Podobnie, jeśli uwzględnimy prawo Daltona:

ν

∆













⋅

=

0

P

P

K

K

x

P

ν

∆





















⋅

=

∑

Y

Y

n

P

n

P

P

K

K

0

gdzie: P oznacza całkowite

ciśnienie równowagowe

∏

=

Y

Y

n

Y

n

K

ν

n

Y

to liczby moli gazów

w stanie równowagi

27

Chem. Fiz. TCH II/06

27

Szczególne przypadki

stałych równowagi (1)

Iloczyn jonowy wody:

K

298

temp.

w

10

14

3

−

=

=

−

+

OH

O

H

w

a

a

K

Stałe kwasowości K

a

i zasadowości K

b

:

(aq)

A

(aq)

O

H

O(c)

H

HA(aq)

3

2

−

+

+

=

+

(aq)

OH

HA(aq)

O(c)

H

(aq)

A

2

−

−

+

=

+

(dla sprzężonej pary kwas-zasada)

HA

O

H

A

a

a

a

a

K

+

−

=

3

−

−

=

A

OH

HA

b

a

a

a

K

w

b

a

K

K

K

=

⋅

Pojęcie pK: pK = –log K

K

298

temp.

w

14

=

=

+

w

b

a

pK

pK

pK

(aq)

OH

(aq)

O

H

O(c)

2H

3

2

−

+

+

=

Iloczyn jonowy wody zwany jest także stałą autodysocjacji lub autoprotolizy
wody.
Oczywiście dotyczy to układów kwasowo zasadowych w roztworach wodnych
(definicja kwasów i zasad wg Brønsteda).

28

Chem. Fiz. TCH II/06

28

Szczególne przypadki

stałych równowagi (2)

Iloczyn rozpuszczalności:

(aq)

yA

(aq)

xM

(s)

A

M

x

y

y

x

−

+

+

=

y

A

x

M

sp

a

a

K

⋅

=

Związek z rozpuszczalnością s wyrażoną w mol/dm

3

:

y

x

y

x

sp

s

y

x

K

+

⋅

⋅

=

29

Chem. Fiz. TCH II/06

29

Szczególne przypadki

stałych równowagi (3)

Stałe tworzenia oraz trwałości (nietrwałości) kompleksów:

O

H

L

O)

M(H

L

M

2

1

n

2

+

=

+

−

O

H

L

O)

M(H

L

L

O)

M(H

2

2

2

n

2

1

n

2

+

=

+

−

−

O

H

ML

L

O)L

M(H

2

n

1

n

2

+

=

+

−

Stałe tworzenia (dla kolejnych reakcji):

[

]

[

] [ ]

L

O)

M(H

L

O)

M(H

n

2

1

n

2

1

⋅

=

−

K

[

]

[

] [ ]

L

O)

M(H

L

O)

M(H

1

n

2

2

2

n

2

2

⋅

=

−

−

K

[

]

[

] [ ]

L

O)L

M(H

ML

1

n

2

n

⋅

=

−

n

K

Zazwyczaj: K

1

< K

2

< ... < K

n

30

Chem. Fiz. TCH II/06

30

Szczególne przypadki

stałych równowagi (4)

Stałe tworzenia oraz trwałości (nietrwałości) kompleksów:

O

H

L

O)

M(H

L

M

2

1

n

2

+

=

+

−

O

H

L

O)

M(H

L

L

O)

M(H

2

2

2

n

2

1

n

2

+

=

+

−

−

O

H

ML

L

O)L

M(H

2

n

1

n

2

+

=

+

−

Stałe trwałości (łączne dla wszystkich reakcji do danego stopnia):

1

1

K

=

β

[

]

[

] [ ]

2

1

2

n

2

2

2

n

2

2

L

O)

M(H

L

O)

M(H

K

K

=

⋅

=

−

β

[

]

[

] [ ]

n

n

K

K

K

...

L

O)

M(H

ML

2

1

n

n

2

n

=

⋅

=

β

Można się także spotkać z pojęciem stałych nietrwałości, które są

odwrotnościami stałych

β

. Ogólnie panuje dość duże zamieszanie

terminologiczne

31

Chem. Fiz. TCH II/06

31

Prężność rozkładowa (1)

Prężnością rozkładową (lub ciśnieniem rozkładowym) nazywamy

prężność cząstkową gazowego produktu rozkładu danej substancji

znajdującego się w równowadze z tą substancją.

Jeżeli w danej temperaturze ciśnienie parcjalne produktu
rozkładu jest wyższe od ciśnienia rozkładowego, reakcja

rozkładu nie zachodzi (lub się cofa), jeśli niższe – zachodzi.

Przykład:

Jakie ciśnienie powstanie i jaki ułamek substancji stałej

się rozłoży, jeśli do sztywnego zbiornika o pojemności 2 dm

3

włoży-

my 20 g czystej kredy (CaCO

3

), ewakuujemy go i ogrzejemy do tem-

peratury 800

o

C?

32

Chem. Fiz. TCH II/06

32

Prężność rozkładowa (2)

Rozwiązanie:

1. Z danych termodynamicznych dla produktów i substratu reakcji

znajduję

∆

G

0

298

=130051 J, co daje K

298

=1,6452·10

-23

. Jak widać,

w temperaturze otoczenia CaCO

3

jest trwały termodynamicznie.

2. Obliczam (przy zmiennym

∆

C

P

) wartość

∆

H

0

1073

(169000 J), co

w porównaniu z

∆

H

0

298

(177886 J) nie jest zbyt dużą różnicą.

Zakładam stałe

∆

H

0

=173500 J.

3. Z równania van’t Hoffa obliczam K

1073

= K

298

·e

50,54706

=0,1474

4. Dla reakcji CaCO

3

(s) = CaO(s) + CO

2

(g), K

P

=P

CO2

/P

0

. Daje to

P

CO2

=14933Pa, oraz 3,35·10

-3

mola CO

2

.

5. Rozłożyła się taka sama liczba moli CaCO

3

, co stanowi 1,67%

jego początkowej ilości (0,2 mola).

6. Uwaga! Dokładne obliczenie

∆

G

0

1073

daje K

1073

=0,3282,

ciśnienie P

CO2

=33245 Pa i 3,73% rozkładu CaCO

3

.

33

Chem. Fiz. TCH II/06

33

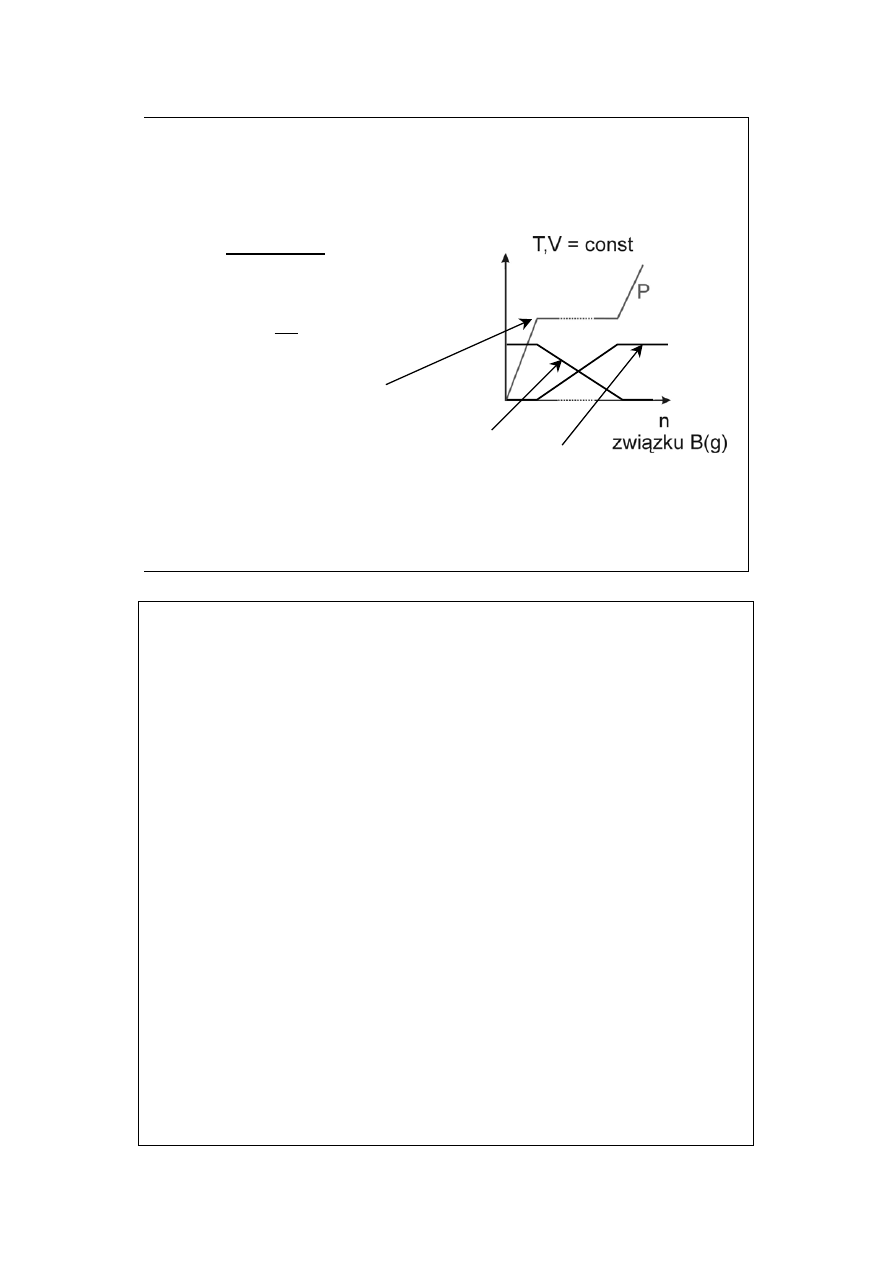
Prężność rozkładowa (3)

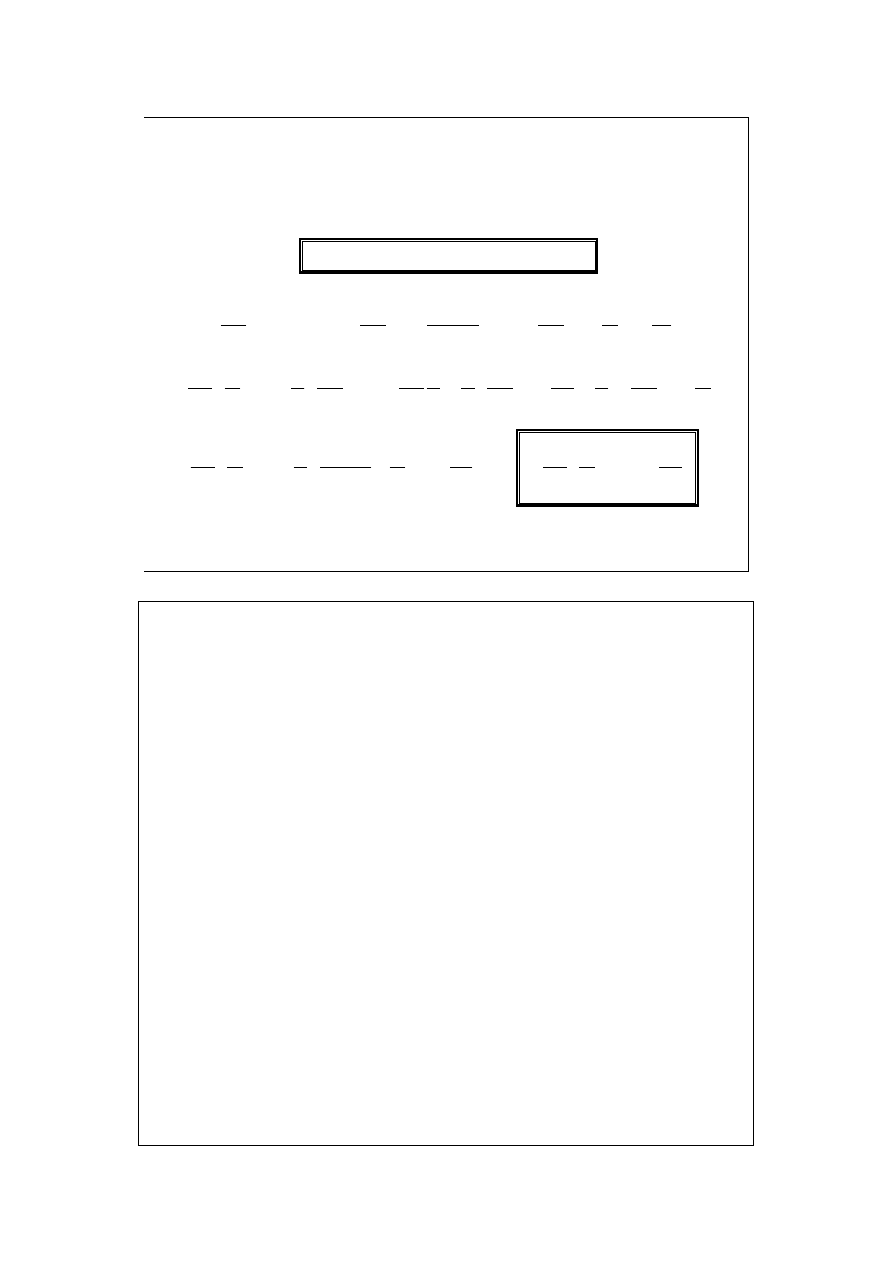
Dla reakcji:

A(s) + B(g) = AB(s), dla której

1

0

−













=

P

P

K

B

P

gdzie: P

B

jest prężnością

rozkładową związku AB

n

A

n

AB

34

Chem. Fiz. TCH II/06

34

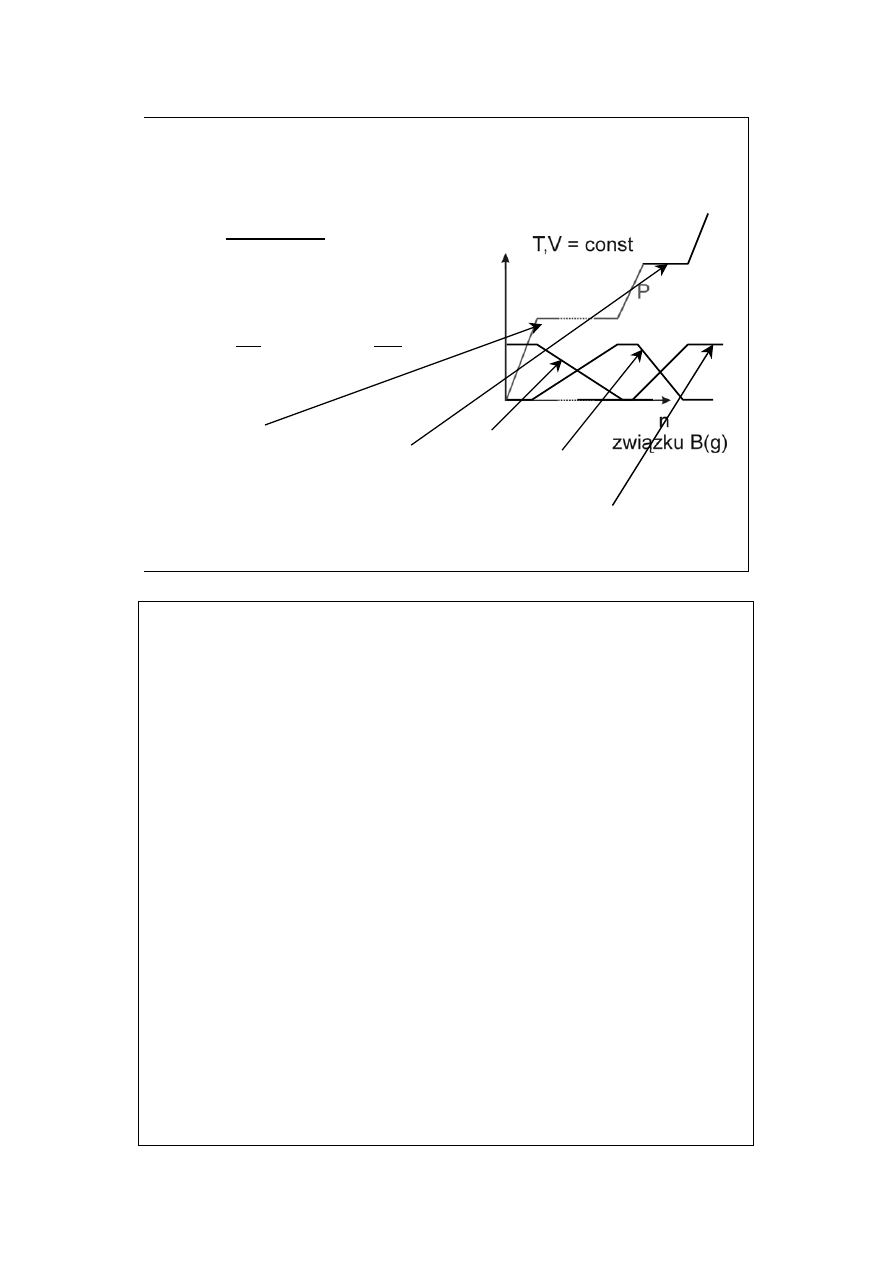
Prężność rozkładowa (4)

Dla reakcji:

A(s) + B(g) = AB(s)

AB(s) + B(g) = AB

2

(s)

1

0

1

1

−













=

P

P

K

B

P

gdzie: P

B1

jest prężnością

rozkładową związku AB, zaś P

B2

–

związku AB

2

n

A

n

AB

1

0

2

2

−













=

P

P

K

B

P

n

AB

2