1

Chem. Fiz. TCH II/05

1

Podstawowe równania –

podsumowanie (1)

Ts

u

f

−

=

w

q

u

+

=

dw

dq

du

+

=

sdT

Tds

du

df

−

−

=

dq

ds

=

T

:

go

odwracalne

procesu

dla

sdT

dq

du

df

−

−

=

:

zatem

dw

dq

du

=

−

:

go)

odwracalne

procesu

(dla

kolei

z

a

sdT

dw

df

−

=

:

wtedy

a

( )

0

:

na

izochorycz

jest

przemiana

jednak

gdy

=

T,V

df

PdV

dw

−

=

( )

dw

df

T

=

:

izotermy

dla

a

To wszystko jest prawdziwe, gdy w układzie nie występuje praca

nie objętościowa!!!

( )

dw

df

dq

Tds

T

<

>

i

:

lnego

nieodwraca

procesu

dla

a

( )

0

:

oraz

<

T,V

df

2

Chem. Fiz. TCH II/05

2

Podstawowe równania –

podsumowanie (2)

Ts

h

g

−

=

PV

u

h

+

=

VdP

PdV

du

dh

+

+

=

sdT

Tds

dh

dg

−

−

=

dq

ds

=

T

:

go

odwracalne

procesu

dla

sdT

VdP

PdV

dw

dg

−

+

+

=

:

zatem

dw

dq

du

=

−

:

i

( )

0

:

ej

izobaryczn

przemiany

dla

,

=

+

=

PdV

dw

dg

P

T

PdV

dw

−

=

:

ponadto

a

( )

VdP

PdV

dw

dg

T

+

+

=

:

izotermy

dla

Prawdziwe, gdy w układzie nie występuje praca nie objętościowa!!!

( )

VdP

PdV

dw

dg

dq

Tds

T

+

+

<

>

i

:

lnego

nieodwraca

procesu

dla

a

( )

0

:

oraz

<

T,P

dg

sdT

Tds

VdP

PdV

du

dg

−

−

+

+

=

3

Chem. Fiz. TCH II/05

3

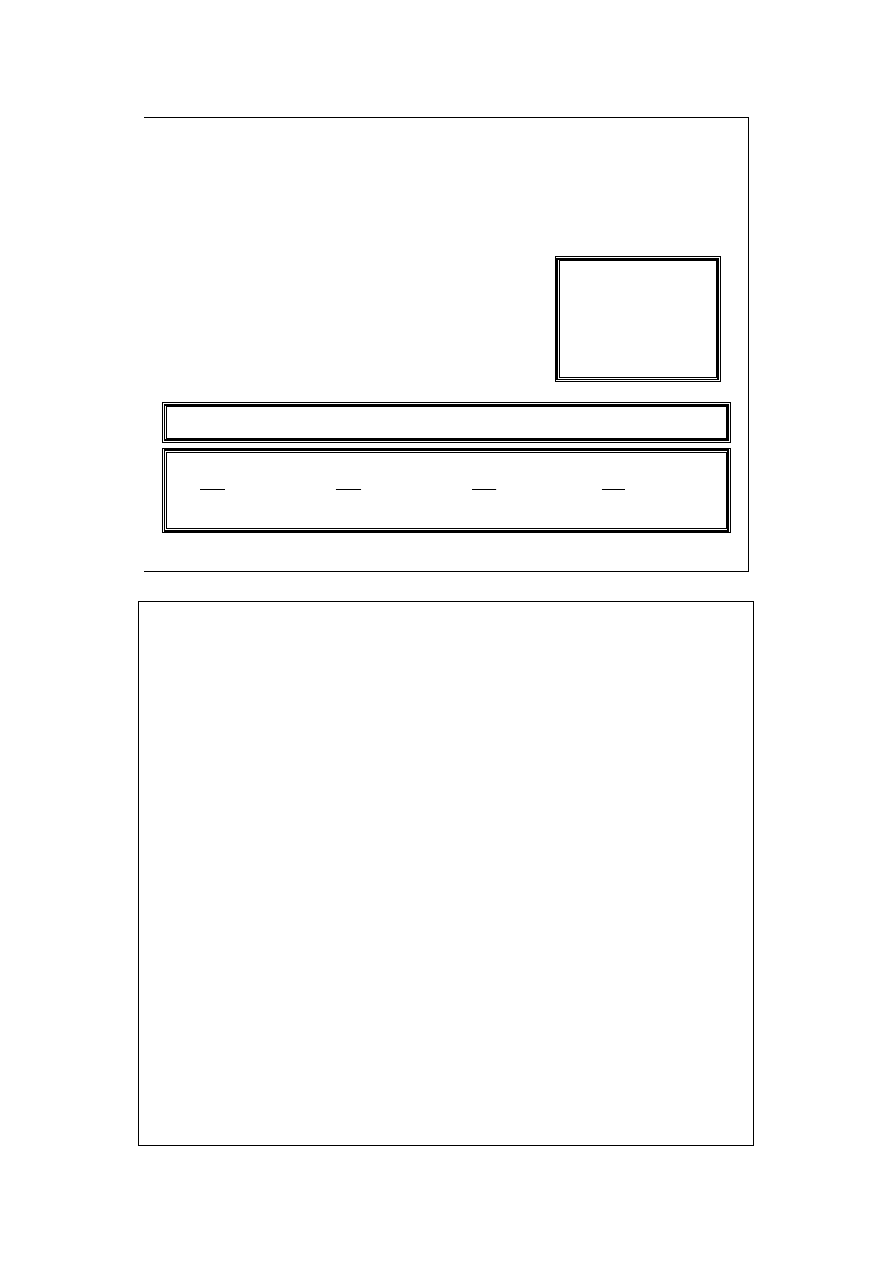
Podstawowe równania –

podsumowanie (3)

(odwr.)

dw

Tds

du

+

=

PdV

Tds

du

−

=

obj.

tylko

praca

gdy

a

Pole powyżej zawiera podstawowe równania termodynamiki.

Ts

h

g

−

=

PV

u

h

+

=

dq

dw

du

+

=

(odwr.)

q

Tds

=

Ts

u

f

−

=

VdP

PdV

du

dh

+

+

=

:

zatem

VdP

Tds

dh

+

=

:

i

sdT

Tds

du

df

−

−

=

:

podobnie

PdV

sdT

df

−

−

=

:

i

sdT

Tds

dh

dg

−

−

=

:

raz

jeszcze

VdP

sdT

dg

+

−

=

:

i

s

T

f

V

−

=













∂

∂

P

V

f

T

−

=













∂

∂

s

T

g

P

−

=













∂

∂

V

P

g

T

=













∂

∂

A w polu różowym są ich konsekwencje ! (równania w żółtym polu są bowiem

różniczkami zupełnymi).

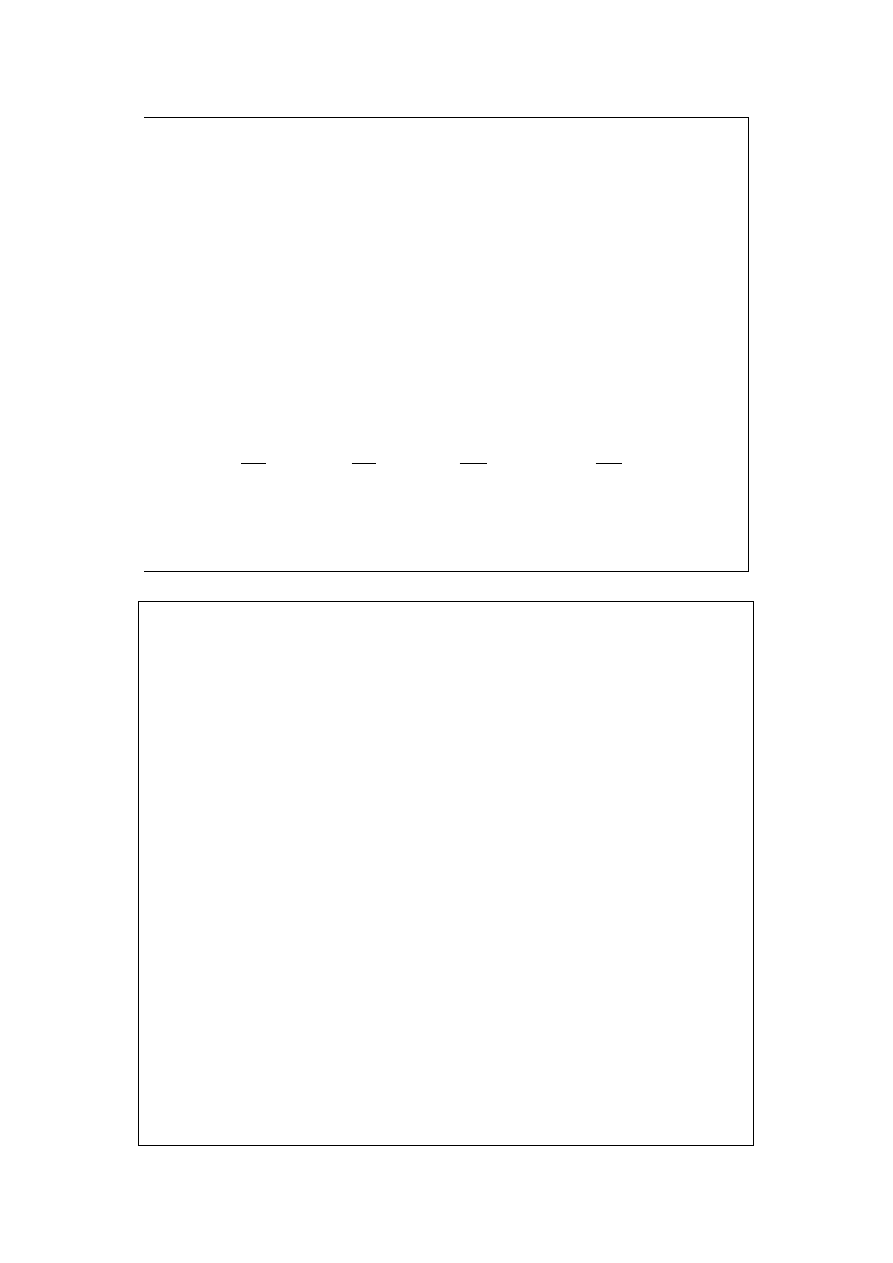
4

Chem. Fiz. TCH II/05

4

Termodynamika układów

otwartych

W układach otwartych, tzn. wymieniających z otoczeniem także

materię, zmienia się ich skład.

Jeśli zawierają one więcej niż jeden, maksymalnie zaś k składników, to

dowolna funkcja stanu musi zależeć od parametrów stanu układu i jego

składu.

)

,...

,...

,

,

,

(

2

1

k

i

n

n

n

n

T

P

f

y

=

W konsekwencji:

i

n

P

T

i

n

P

T

n

T

n

P

dn

dn

dy

dn

dn

dy

dP

dP

dy

dT

dT

dy

dy

i

j

j

i

i

≠

≠













+













+













+













=

,

,

1

,

,

1

,

,

1

Ostatni człon wyrażenia na różniczkę zupełną jest kluczowy dla zrozumienia

istoty zagadnienia. Oznacza on infinitezymalną zmianę stężenia (zawartości)
składnika i, przy niezmiennych stężeniach (zawartościach) pozostałych
składników układu.

5

Chem. Fiz. TCH II/05

5

Cząstkowe molowe

wielkości (1)

Wielkości określone pochodną:

i

j

n

P

T

i

dn

dy

≠













,

,

nazywamy cząstkowymi molowymi wielkościami:

i

j

n

P

T

i

i

dn

dy

Y

≠













=

,

,

za pomocą których możemy opisać zmiany stanu układu otwartego:

k

k

i

i

n

T

n

P

dn

Y

dn

Y

dn

Y

dP

dP

dy

dT

dT

dy

dy

i

i

+

+

+

+

+













+













=

...

...

1

1

,

,

W szczególności, w warunkach

izotermiczno-izobarycznych:

∑

=

=

k

i

i

i

dn

Y

dy

1

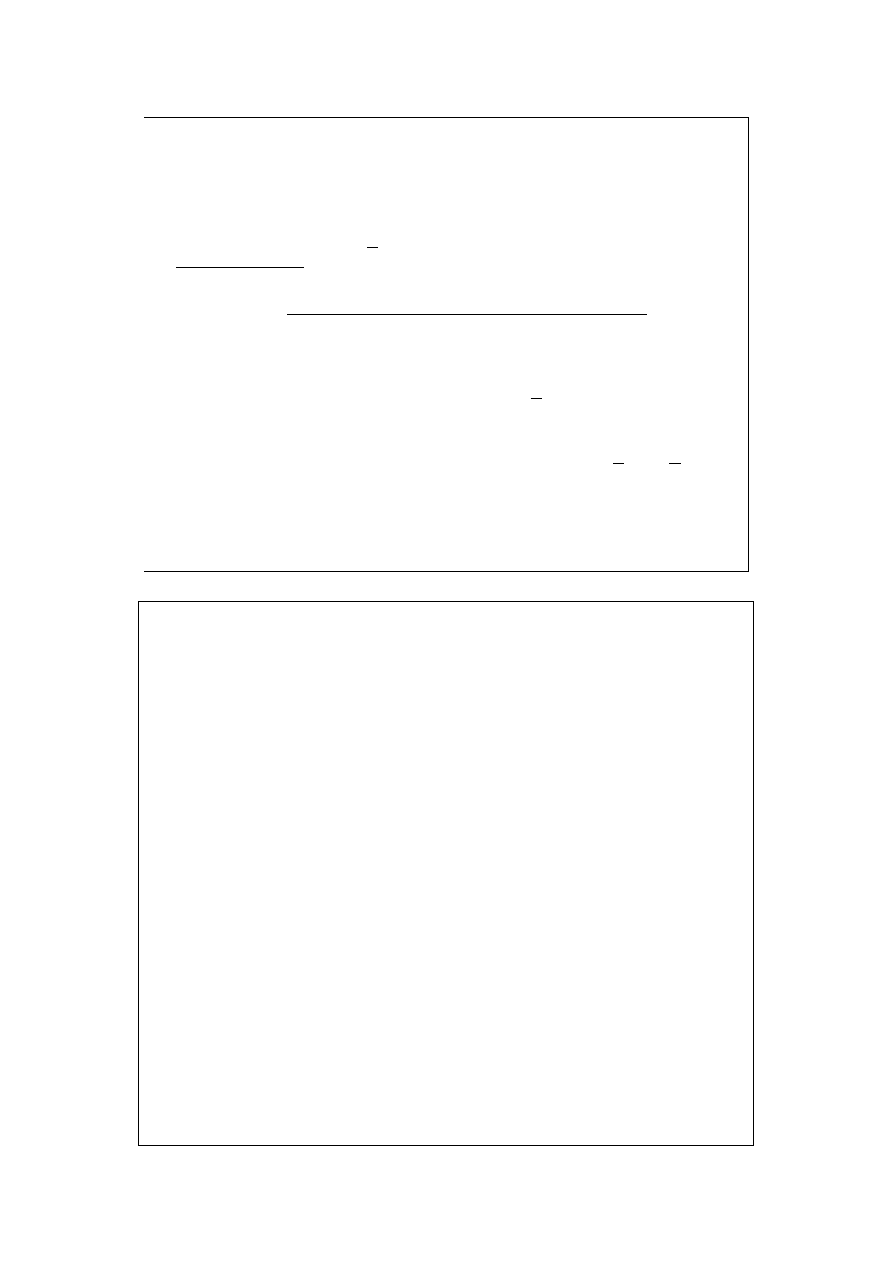
6

Chem. Fiz. TCH II/05

6

Cząstkowe molowe

wielkości (2)

Można ją więc scałkować (po dowolnej drodze) od stanu

n

i

=0 do stanu n

i

(końcowe). Droga ta może być taka, aby:

const

Y

i

=

_

W tych warunkach:

∑

=

k

i

i

i

dn

Y

1

jest różniczką zupełną funkcji y

ergo, funkcją stanu układu, zależną od jego składu.

W wyniku czego otrzymujemy:

∑

=

=

k

i

i

i

Y

n

y

1

∑

∑

=

=

+

=

k

i

i

i

k

i

i

i

dn

Y

Y

d

n

dy

1

1

zaś najogólniejsze wyrażenie na jej

różniczkę zupełną dane jest równaniem:

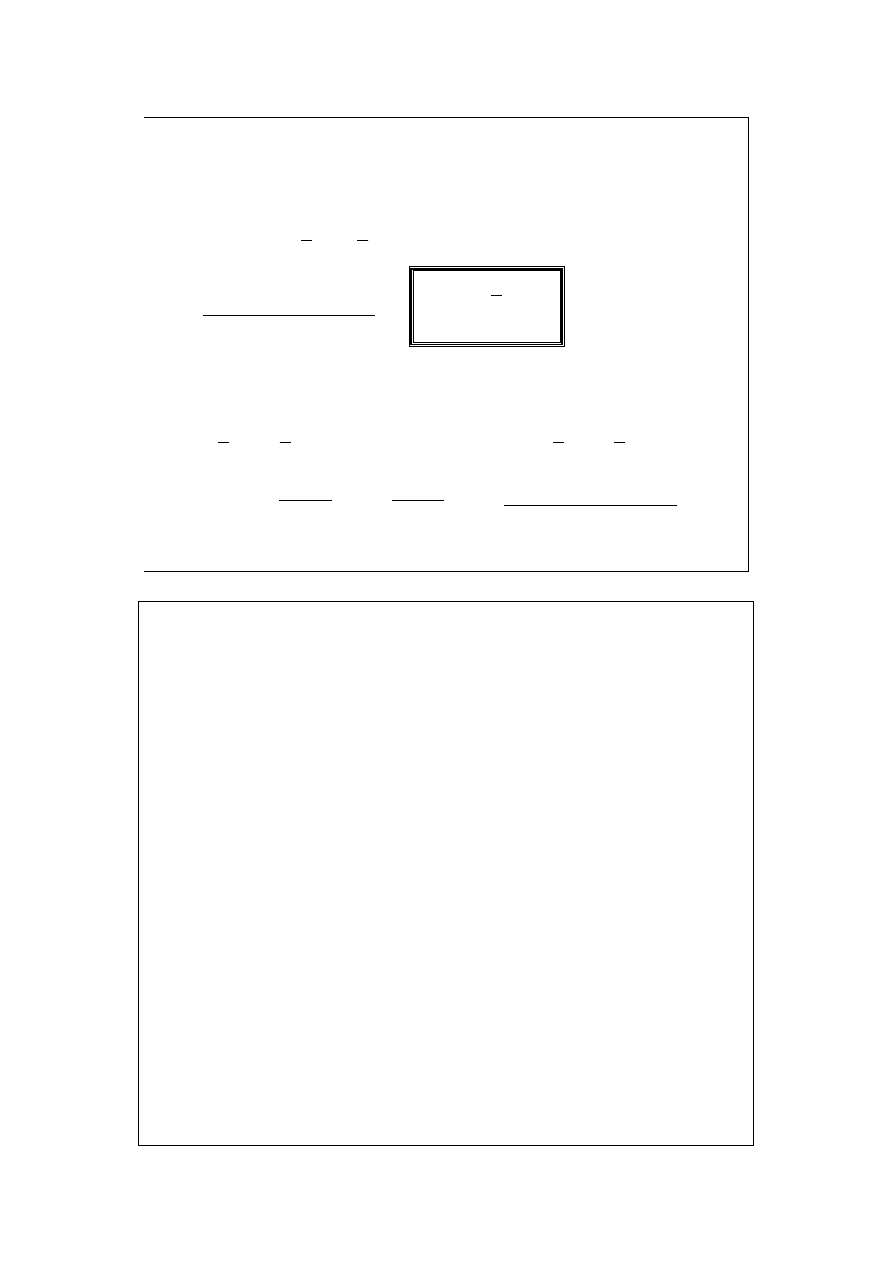
7

Chem. Fiz. TCH II/05

7

Równanie Gibbsa-Duhema

Ostatnie wyrażenie nosi nazwę równania Gibbsa-Duhema.

Jeśli:

∑

∑

=

=

+

=

k

i

i

i

k

i

i

i

dn

Y

Y

d

n

dy

1

1

a równocześnie:

∑

=

=

k

i

i

i

dn

Y

dy

1

_

ergo, musi być prawdziwe:

0

1

=

∑

=

k

i

i

i

Y

d

n

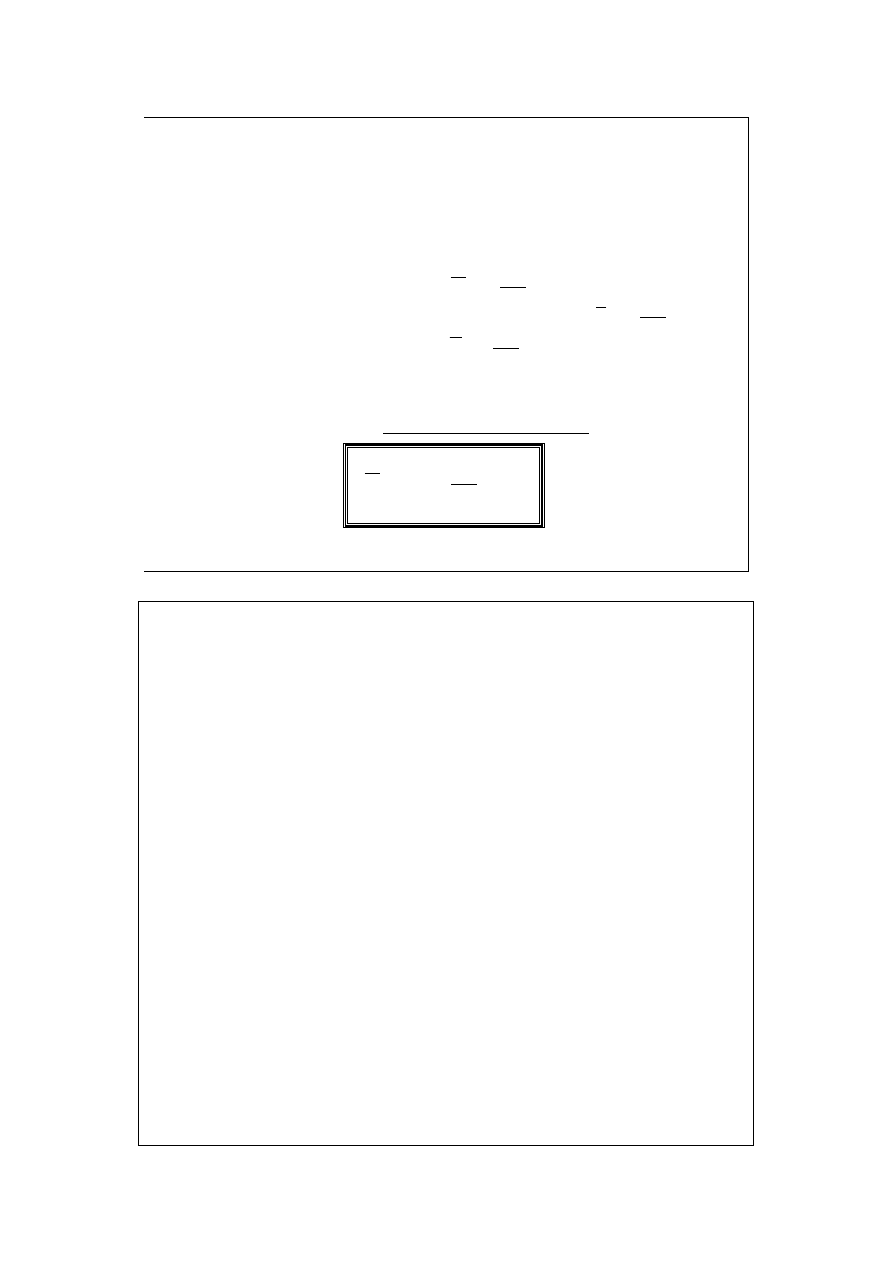
Dla układu dwuskładnikowego, można je wyrazić:

0

2

2

1

1

=

+

Y

d

n

Y

d

n

0

2

2

1

1

=

+

Y

d

x

Y

d

x

lub:

gdzie:

2

1

2

2

2

1

1

1

;

n

n

n

x

n

n

n

x

+

=

+

=

są ułamkami molowymi
składników 1 i 2.

8

Chem. Fiz. TCH II/05

8

Cząstkowe molowe

wielkości (3)

Najczęściej stosowane cząstkowe molowe wielkości to:

cząstkowa molowa entalpia:

i

j

n

P

T

i

i

n

h

H

≠













∂

∂

=

,

,

cząstkowa molowa entropia:

i

j

n

P

T

i

i

n

s

S

≠













∂

∂

=

,

,

cząstkowa molowa objętość:

i

j

n

P

T

i

i

n

v

V

≠













∂

∂

=

,

,

i najważniejsza z nich, cząstkowa molowa entalpia swobodna,

zwana też potencjałem chemicznym:

i

j

n

P

T

i

i

i

n

g

G

≠













∂

∂

=

=

,

,

µ

9

Chem. Fiz. TCH II/05

9

Cząstkowe molowe

wielkości (4)

Zależności pomiędzy cząstkowymi molowymi wielkościami są

analogiczne do zachodzących pomiędzy h, s, v i g.

Np., różniczkując względem n

i

wyrażenie:

Ts

h

g

−

=

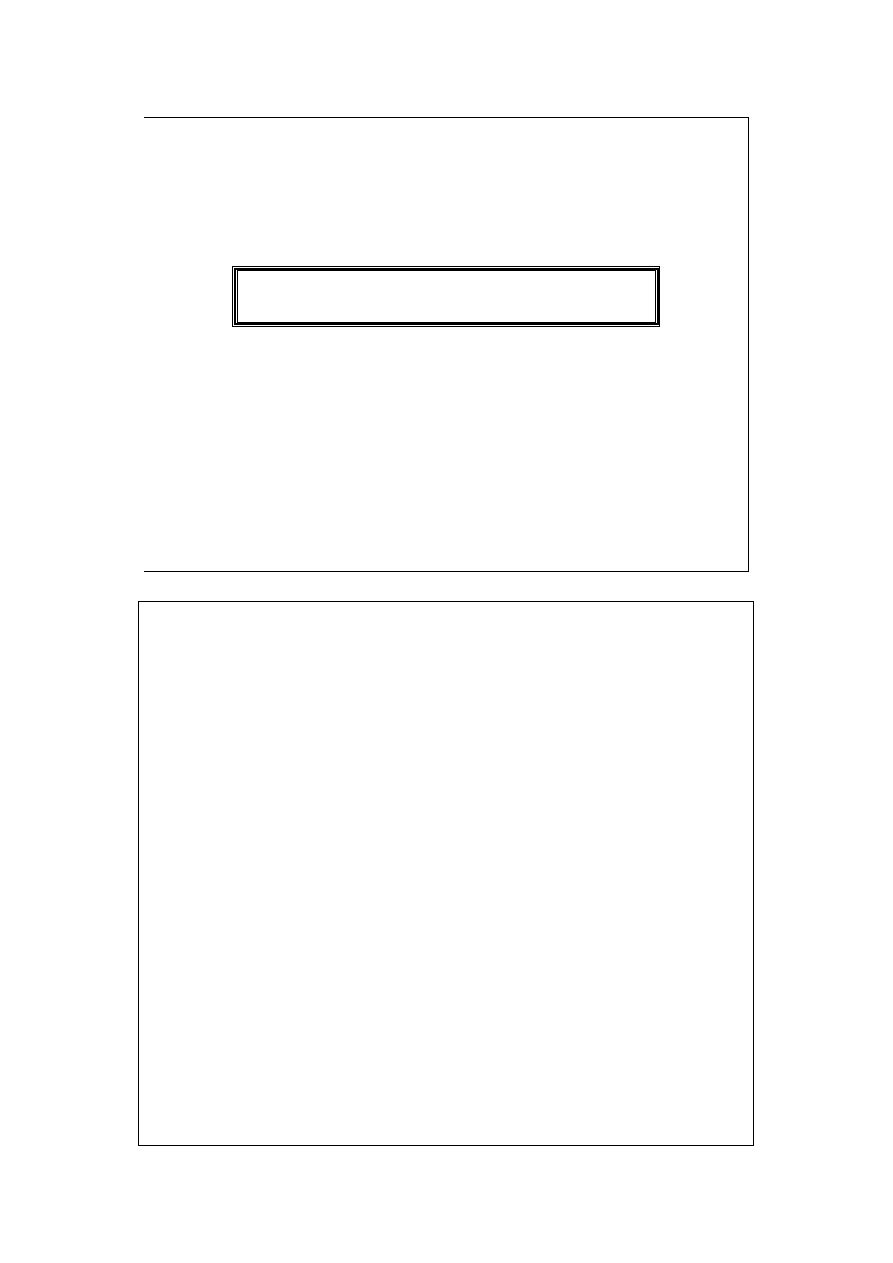
otrzymujemy:

=

−

=

=

∂

∂

−

∂

∂

=

∂

∂

i

i

i

i

i

i

S

T

H

n

s

T

n

h

n

g

µ

a wychodząc z zależności:

s

T

g

P

−

=













∂

∂

otrzymamy:

S

T

n

s

n

T

g

i

i

i

−

=

∂

∂

=

∂

∂

−

=

∂

∂

∂

µ

2

10

Chem. Fiz. TCH II/05

10

Cząstkowe molowe

wielkości (5)

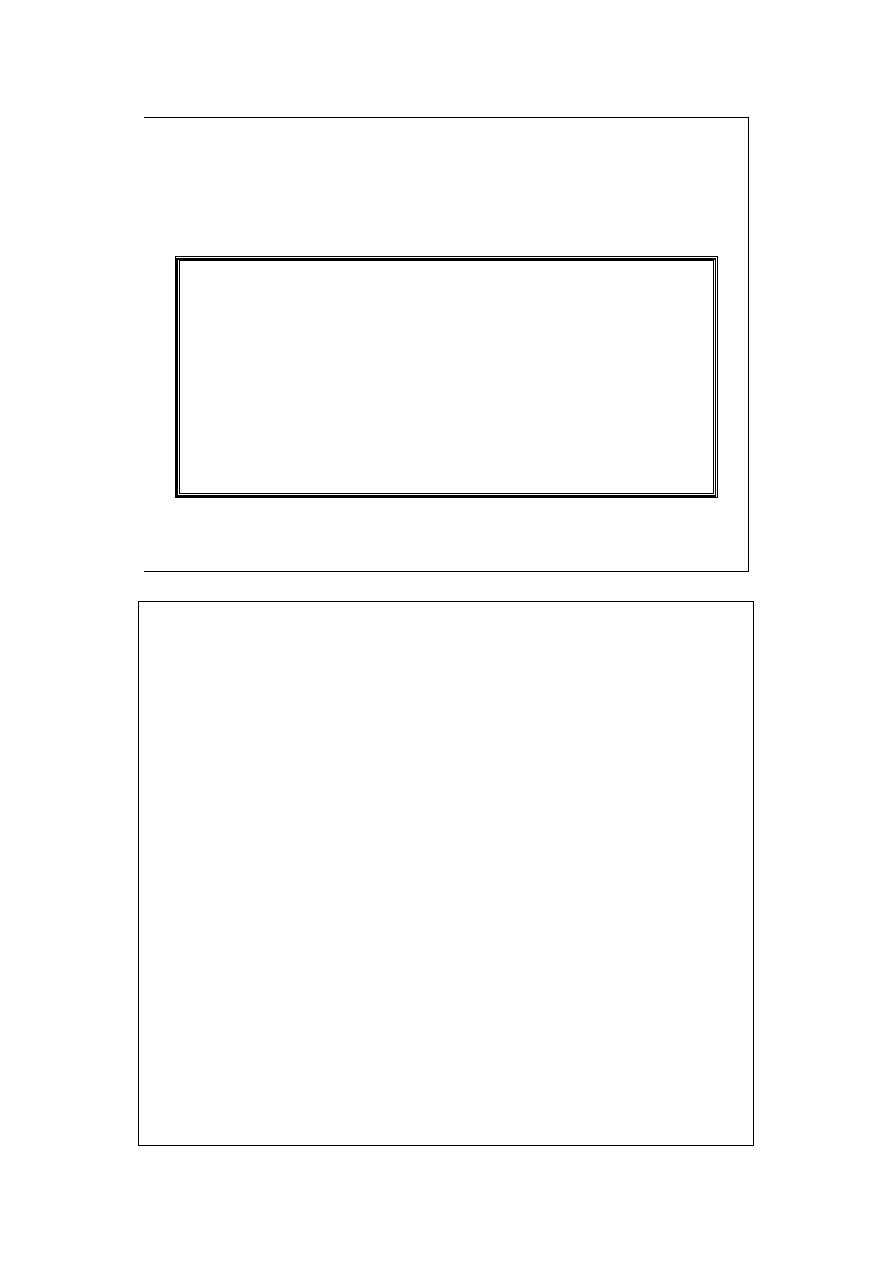
Najważniejsza zależność termodynamiki chemicznej:

k

k

i

i

dn

dn

dn

SdT

VdP

dG

µ

µ

µ

+

+

+

+

+

−

=

...

...

1

1

Pod stałym ciśnieniem i w stałej temperaturze:

k

k

i

i

dn

dn

dn

dG

µ

µ

µ

+

+

+

+

=

...

...

1

1

A wtedy, praca nieobjętościowa może być spowodowana zmianą

składu chemicznego układu. Np. w ogniwie galwanicznym zmiana

jego składu chemicznego (od substratów do produktów) prowadzi

do uzyskania pracy elektrycznej.

11

Chem. Fiz. TCH II/05

11

Gazy

Zagadnienia omawiane w tej części, przynajmniej w

pewnym zakresie, traktuję jako powtórkę.

Niektóre przeźrocza w tej serii są zatem jedynie

materiałem pomocniczym!

Większość omawianych tutaj zagadnień można

(i należy) powtórzyć sobie z dowolnego podręcznika

chemii fizycznej lub fizyki.

12

Chem. Fiz. TCH II/05

12

Gaz doskonały(1).

Prawa gazowe

Boyle’a

izoterma

const

T

const

PV

=

=

dla

;

Charlesa

izobara

const

P

T

V

=

∝

dla

;

Gay-Lussaca

izochora

const

V

T

P

=

∝

dla

;

Równanie Clapeyrona

nRT

PV

=

T

PV

R

m

P 0

lim

→

=

Jeśli ktoś chce „wyprowadzać” równanie Clapeyrona, to może to uczynić

wykorzystując fakt, że dwa dowolne punkty na płaszczyźnie P-V można zawsze
połączyć jedną izotermą i jedną izochorą (lub izobarą).

W odniesieniu do gazów rzeczywistych – równanie Clapeyrona (podobnie jak
cząstkowe prawa gazowe) ma charakter graniczny! Dlatego te ostatnie
nazywamy często „prawami gazów rozrzedzonych”.

13

Chem. Fiz. TCH II/05

13

Gaz doskonały(2).

Prawa gazowe, c.d.

Avogadro

n

const

V

⋅

=

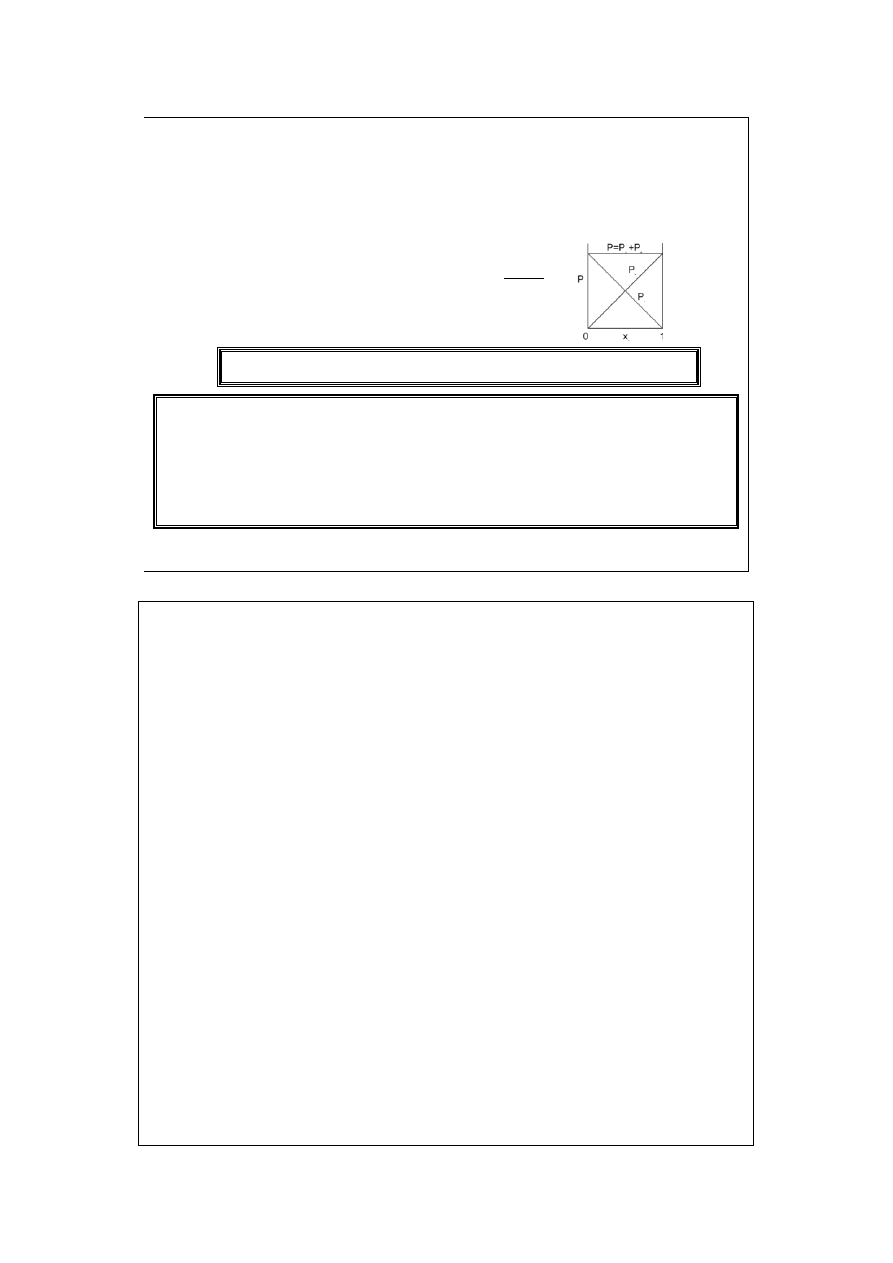
Daltona

;

;

1

i

i

k

i

i

x

P

P

P

P

⋅

=

=

∑

=

∑

=

=

k

i

i

i

i

n

n

x

1

Założenia kinetycznego modelu gazu doskonałego:

•

Cząsteczki gazu, o masie m znajdują się w ciągłym, chaotycznym

ruchu.

•

Jedyne oddziaływanie pomiędzy cząsteczkami, jak również

między nimi a ścianką zbiornika to zderzenia idealnie sprężyste.

•

Rozmiary cząsteczek są pomijalnie małe w porównaniu ze średnią

drogą pomiędzy zderzeniami (średnią drogą swobodną).

Od prawa Avogadro są odstępstwa. Tylko gaz doskonały ma objętość molową

dokładnie 22,4 dm

3

/mol w 273,15K, pod normalnym ciśnieniem.

14

Chem. Fiz. TCH II/05

14

Gaz doskonały(3).

Ciśnienie wg modelu kinetycznego

1

2

mv

mv

t

F

−

=

∆

Druga zasada dynamiki Newtona:

V

nN

t

Av

l

A

x

∆

=

2

1

Liczba cząsteczek uderzających w ściankę o pow.

A

w czasie

∆

t

(zmiana szybkości z mv

x

na – mv

x

):

Ich masa (masa jednej cząsteczki to M/N

A

) :

Ich całkowita zmiana pędu :

V

nM

t

Av

lm

x

∆

=

2

1

V

nM

t

Av

t

F

x

∆

=

∆

2

Wywierane ciśnienie (F/A) :

V

nM

v

P

x

2

=

Ponieważ :

2

2

2

2

z

y

x

v

v

v

c

+

+

=

To ostatecznie :

nM

c

PV

2

3

1

=

n oznacza liczbę moli w objętości V.

Składowe szybkości są równe we wszystkich kierunkach (x, y i z).
Otrzymaliśmy więc prawo Boyle’a (dla stałej T, średnia szybkość kwadratowa
jest stała, jak zobaczymy z rozkładu Maxwella).
Słuszność ostatniej zależności potwierdzono doświadczalnie (Stern) mierząc c.
Wielkość c nazywamy średnią szybkością kwadratową.
W ten sposób otrzymaliśmy - na drodze rozważań z fizyki klasycznej – prawo
Boyle’a.

15

Chem. Fiz. TCH II/05

15

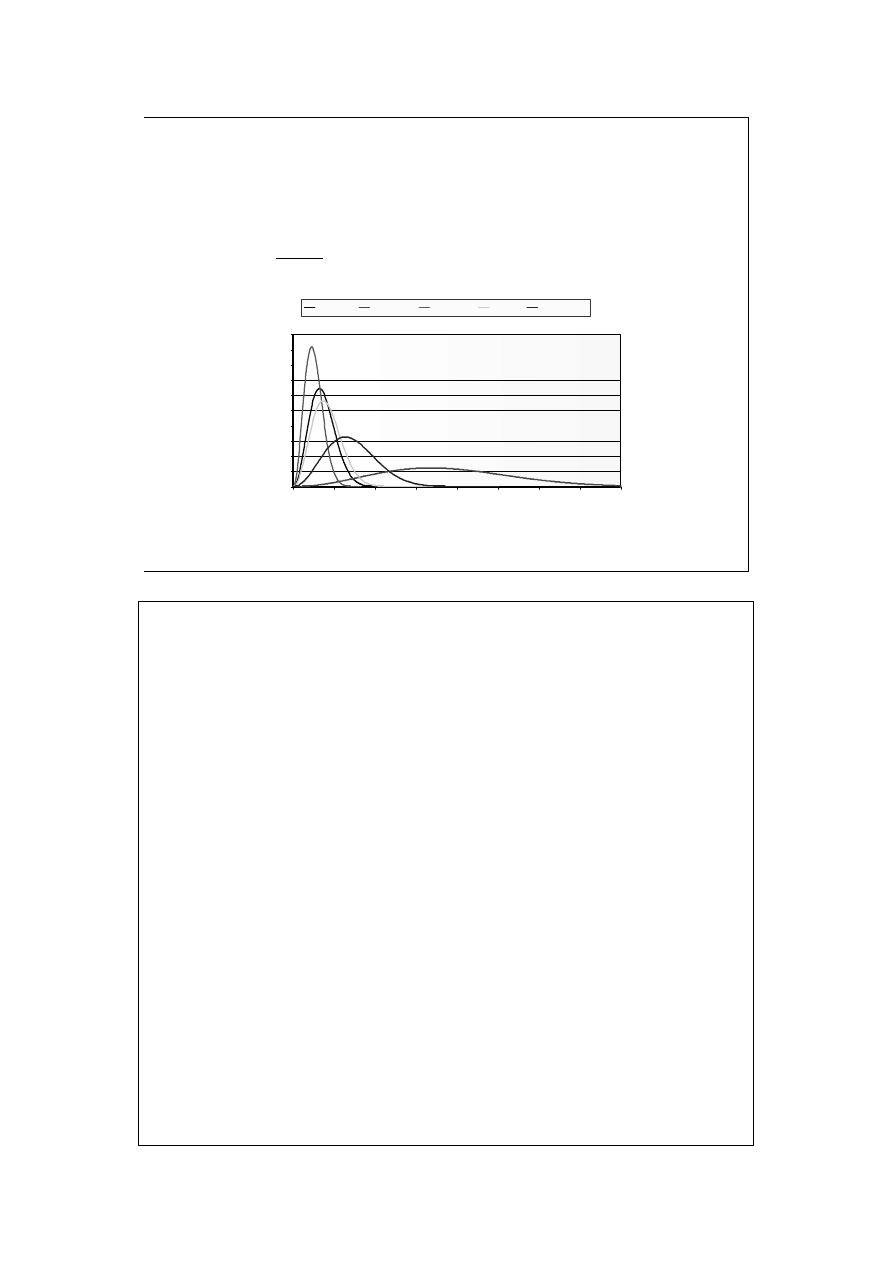
Rozkład Maxwella (1)

0

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

0,18

0,2

0

10

20

30

40

50

60

70

80

s zybkoś ć, m/s

wz

g

lę

dna

l

ic

z

ba

c

z

ą

st

e

c

z

e

k

He; 10 K

He; 273 K

Rn; 273 K

Kr; 273

Azot;273 K

)

2

/(

2

2

/

3

2

2

4

)

(

RT

Mv

e

v

RT

M

v

f

−













=

π

π

bez wyprowadzania

Z wykresu widzimy jakie szybkości osiągają cząsteczki w temperaturze 0

o

C

Wtedy widzimy zależność od masy molowej.
Na przykładzie helu pokazano też zależność od temperatury.

Oś y jest właściwie osią gęstości prawdopodobieństwa. Całka z rozkładu
Maxwella od 0 do

∞ wynosi 1.

Maksimum rozkładu wskazuje nam szybkość najbardziej prawdopodobną.
Wysokość powyżej której pole równa się polu poniżej - odpowiada szybkości
średniej (jednakowe prawdopodobieństwo większych i mniejszych szybkości,
połowa cząsteczek ma szybkość wyższą, połowa niższą).

16

Chem. Fiz. TCH II/05

16

Rozkład Maxwella (2)

2

/

1

3













=

M

RT

c

Wykorzystując rozkład Maxwella można także wyznaczyć

takie własności cząsteczek gazu jak:

szybkość średnia kwadratowa :

szybkość średnia :

szybkość najbardziej prawdopodobna:

średnia szybkość względna:

częstość zderzeń:

średnia droga swobodna:

2

/

1

8













=

M

RT

c

π

2

/

1

2

*













=

M

RT

c

2

/

1

8

2













=

⋅

=

πµ

kT

c

c

wzgl

kT

P

c

V

N

c

z

wzgl

wzgl

⋅

=

⋅

=

σ

σ

P

kT

z

c

σ

λ

2

=

=

Wzór na średnią szybkość kwadratową wynika już z samego modelu
kinetycznego. Jeśli ostateczną postać wyrażenia na PV porównamy z równaniem
gazu doskonałego, to jej prawa strona musi równać się nRT (i stąd wzór).
Średnia szybkość względną to szybkość cząsteczek gazu względem siebie
(zbliżania się lub oddalania).

Wielkość

µ to masa zredukowana dwóch mijających się cząsteczek:

µ=m

1

m

2

/(m

1

+m

2

).

Wielkość

σ to przekrój czynny na zderzenie: σ = πd

2

.

17

Chem. Fiz. TCH II/05

17

Gazy rzeczywiste. Równanie

stanu Van der Waalsa

nRT

PV

=

Udoskonalenie (urealnienie) równania Clapeyrona:

na 1 mol gazu:

Poprawka na objętość mola cząsteczek gazu, b

m

V

RT

P

=

b

V

RT

P

m

−

=

Poprawka na oddziaływania międzycząsteczkowe, a

2

m

m

V

a

b

V

RT

P

−

−

=

• same cząsteczki gazu zajmują pewną objętość, b

• atraktywne (przyciągające) oddziaływania międzycząsteczkowe zmniejszają pęd

(zatem siłę) cząsteczek zmierzających ku ściance, a także częstość ich zderzeń ze

ścianką, dodatkowo zmniejszają więc ciśnienie (do kwadratu stężenia cząsteczek).

Wyprowadzenie równania van der Waalsa:
Poprawka b, ma zatem wymiar m

3

/mol (najmniejsza jest dla Ne < He < H

2

).

Oddziaływania międzycząsteczkowe zależą od stężenia cząsteczek gazu, które
jest odwrotnością objętości molowej. Z tego względu, druga poprawka musi
mieć wymiar Pa·m

-6

·mol

2

. Poprawka a najmniejsza jest dla He < Ne < H

2

.

Johannes Diederik van der Waals otrzymał nagrodę Nobla z fizyki w 1910 roku.

18

Chem. Fiz. TCH II/05

18

Izotermy Van der Waalsa

(1)

punkt krytyczny

b

V

c

3

=

2

27b

a

P

c

=

bR

a

T

c

27

8

=

Związki między

współczynnikami r-nia Van

der Waalsa a parametrami

krytycznymi:

Związki te łatwo wyprowadzić przekształcając równanie Van der Waalsa do
postaci wielomianu trzeciego stopnia względem V

c

i przyrównując go z

rozwinięciem wielomianu (V-V

c

)

3

=0.

Ten ostatni wynika z warunku, że dla punktu krytycznego wszystkie trzy
pierwiastki równania powinny być identyczne (jeden potrójny pierwiastek).
Znaczenie temperatury krytycznej. Powyżej tej temperatury nie da się skroplić
gazu, choćby stosując największe ciśnienia.
Równanie Van der Waalsa nadszacowuje objętość krytyczną.

19

Chem. Fiz. TCH II/05

19

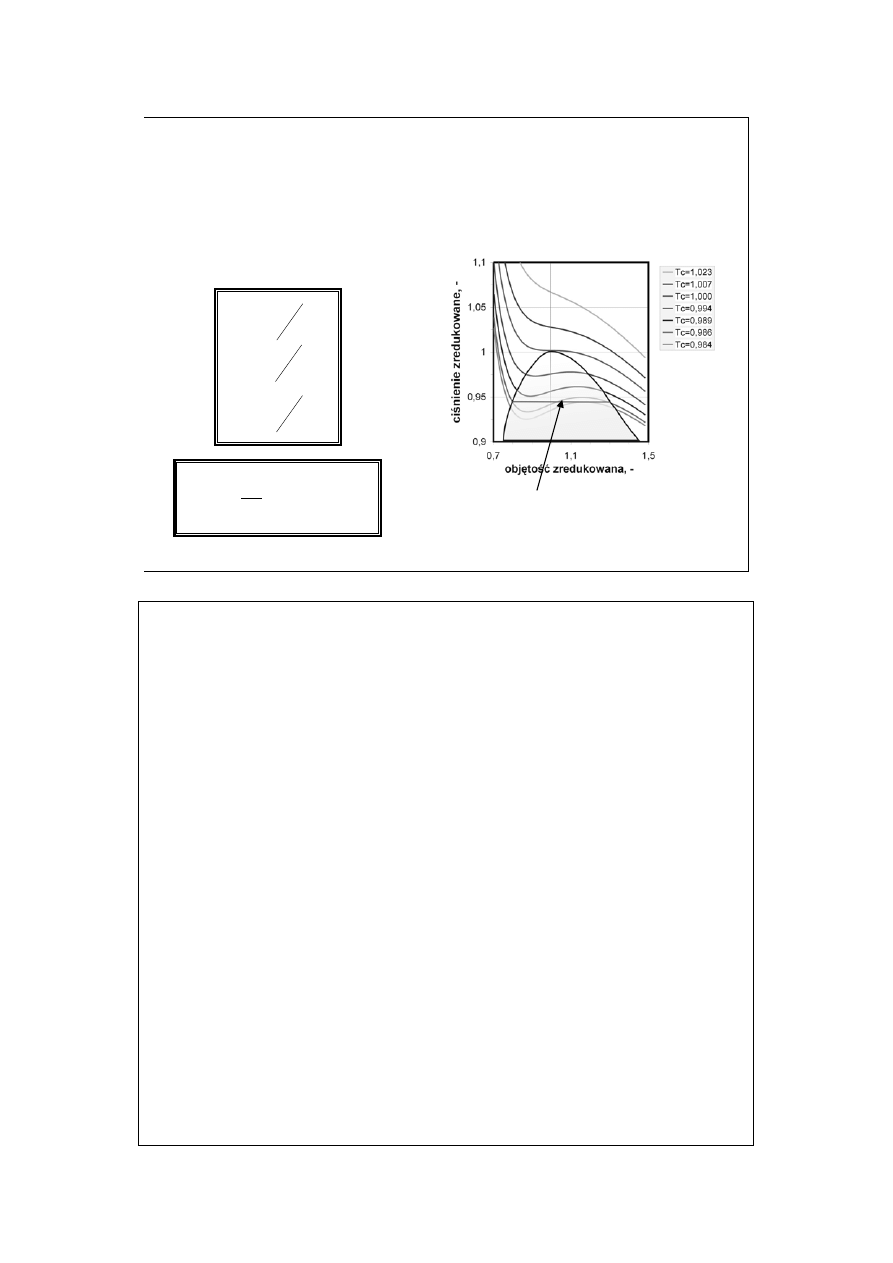
Izotermy Van der Waalsa

(2)

c

P

P

=

π

c

V

V

=

φ

c

T

T

=

θ

rzeczywisty przebieg

izotermy podczas skraplania

zredukowane parametry stanu

i równanie Van der Waalsa

(

)

θ

φ

φ

π

8

1

3

3

2

=

−











 +

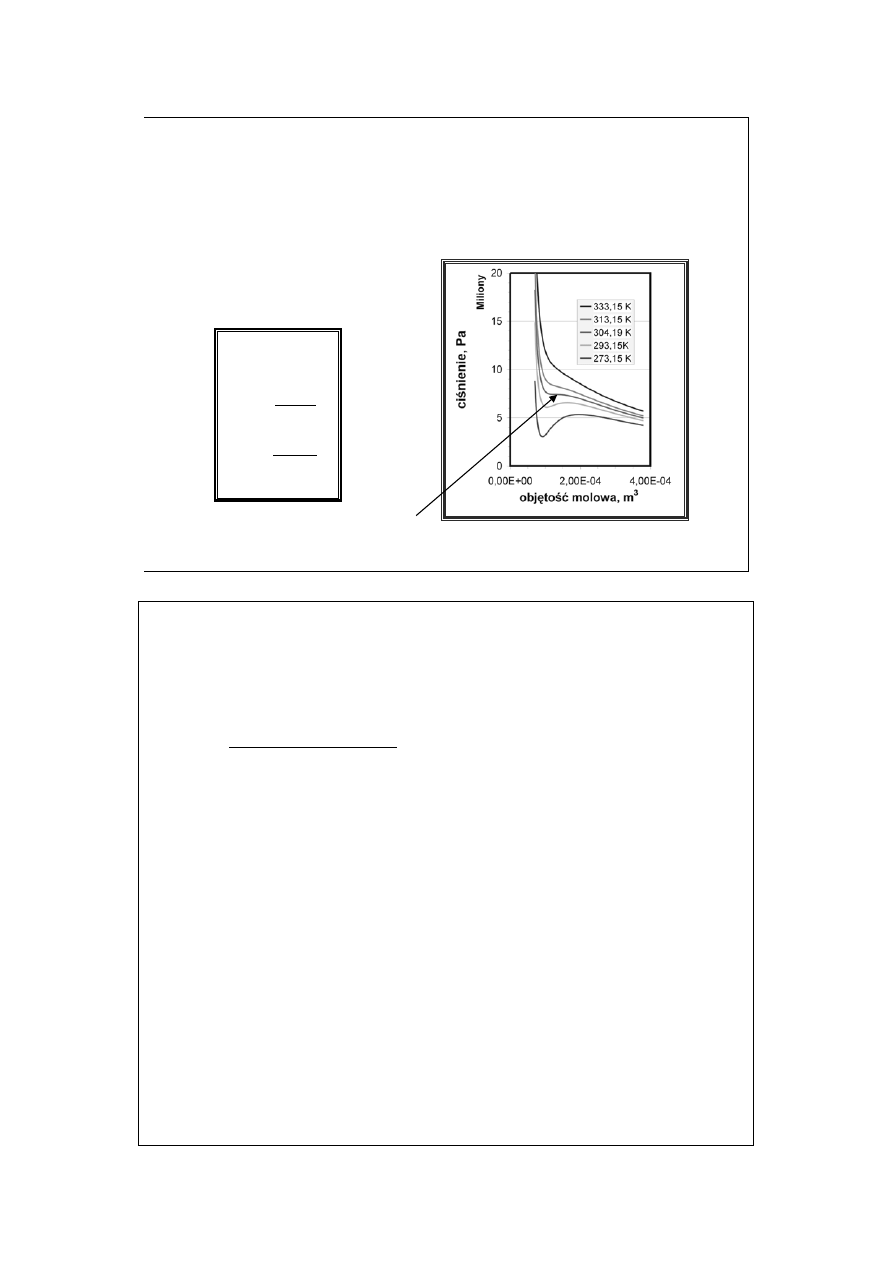
Obszar cieniowany wskazuje rejon współistnienia fazy ciekłej i gazowej.
„Pętle Van der Waalsa” są artefaktami, prawdziwy przebieg izotermy pokazuje
poziomy odcinek prostoliniowy. Prowadzi się go tak, aby powierzchnie pod
dodatnią i nad ujemną częścią pętli były jednakowe.
Znaczenie gazu w stanie nadkrytycznym w analityce (ekstrakcja, chromatografia
w stanie nadkrytycznym łącząca zalety cieczowej i gazowej).

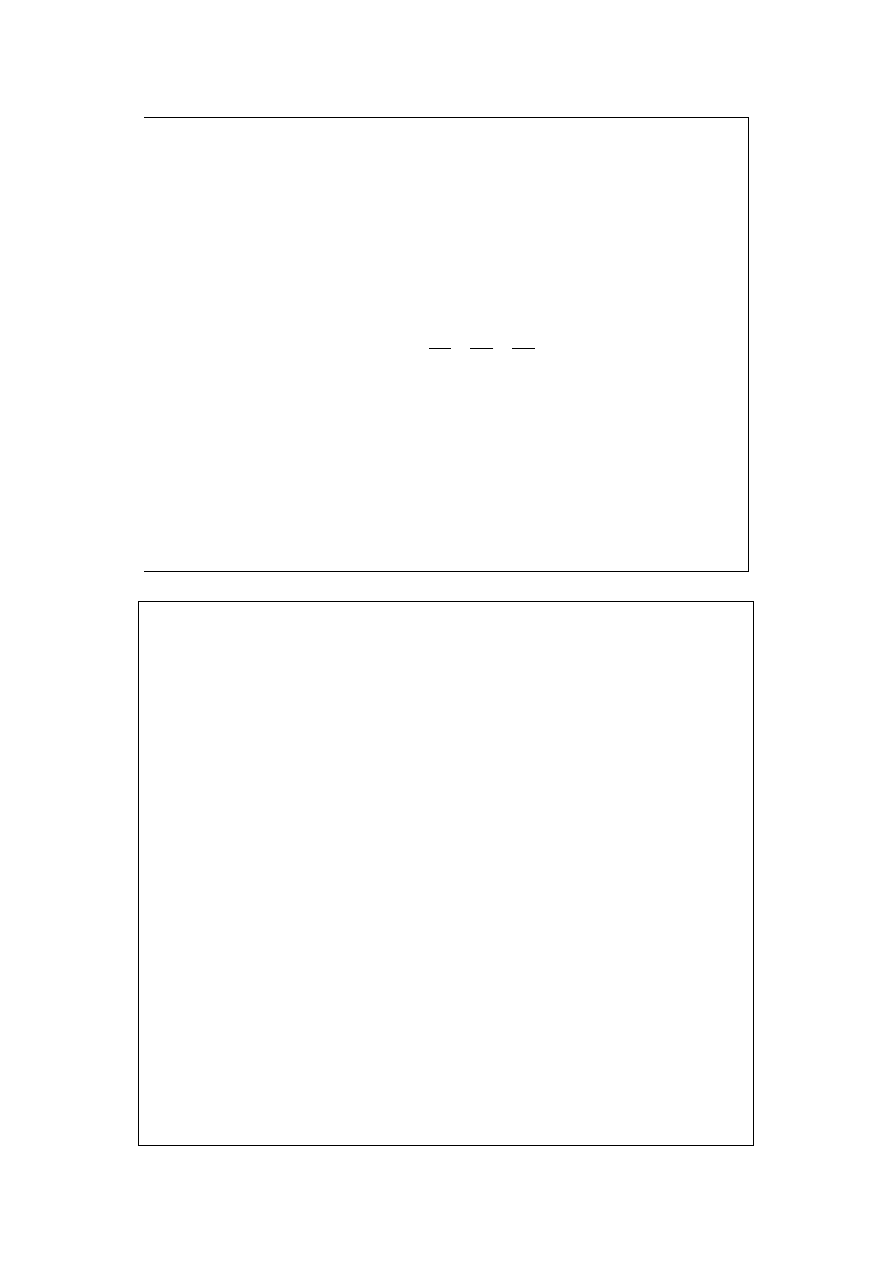
20

Chem. Fiz. TCH II/05

20

Wirialne równania stanu

...)

'

'

'

1

(

3

2

+

+

+

+

=

P

D

P

C

P

B

RT

PV

m













+

+

+

+

=

...

1

3

2

m

m

m

m

V

D

V

C

V

B

RT

PV

Zaproponował je Kamerlingh Onnes (dwie formy):

Współczynniki B, C, D (B’, C’, D’) noszą nazwę

współczynników wirialnych (zależą od temperatury).

Często stosuje się jedynie drugi współczynnik wirialny:

P

B

RT

PV

m

"

+

=

Z powodu niedoskonałości równania Van der Waalsa zaproponowano szereg
innych równań stanu (Berthelota, Dietericiego, Beattiego-Bridgemana).
Niedogodność równania wirialnego (zależność współczynników od T).
Zastosowane tutaj podejście (rozwijanie w szereg potęgowy) jest często
spotykane w chemii fizycznej. Pierwszy człon daje równanie gazu doskonałego.

21

Chem. Fiz. TCH II/05

21

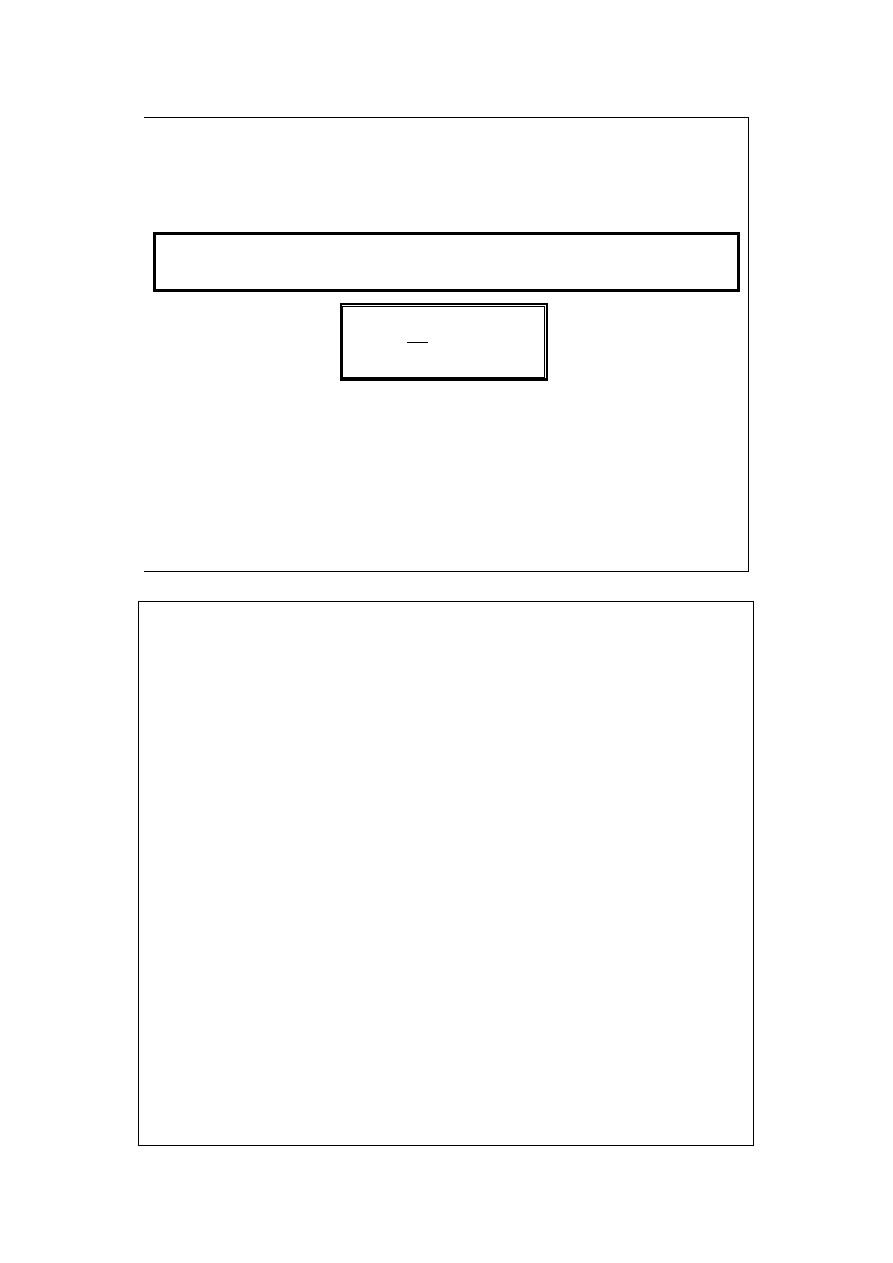
Gazy rzeczywiste w tych samych warunkach zredukowanej objętości

i temperatury wywierają takie samo ciśnienie zredukowane.

Zasada stanów

odpowiadających sobie

Wynika ze zredukowanego r-nia Van der Waalsa (znikają w nim

bowiem charakterystyczne dla poszczególnych gazów współczynniki

a

i b). Inne równania stanu też ją zawierają.

Zasada ta zawodzi, gdy cząsteczki gazu są nie sferyczne lub polarne.

(

)

θ

φ

φ

π

8

1

3

3

2

=

−











 +

22

Chem. Fiz. TCH II/05

22

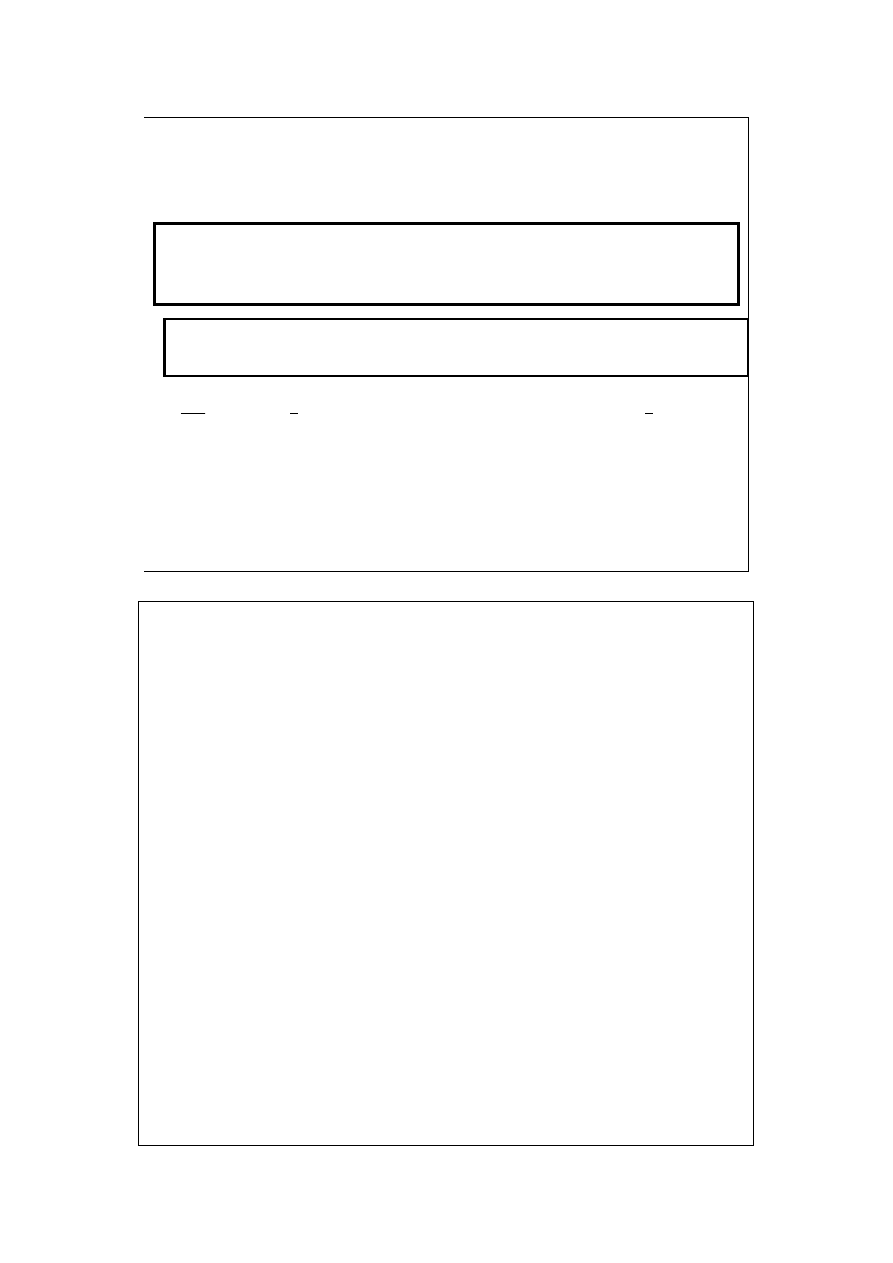
Skraplanie gazów. Efekt

Joule’a-Thomsona (1).

Klasyczne metody sprężania poniżej w temperaturze T<T

c

często nie

wystarczały do skroplenia gazów o coraz niższych T

c

.

q = 0

adiabatyczne

rozprężanie

-w = P

2

V

2

– P

1

V

1

James Joule

rura izolowana

termicznie

przegroda

porowata

P

1

,T

1

P

2

,T

2

U

2

– U

1

= P

2

V

2

– P

1

V

1

U

2

+ P

2

V

2

= U

1

+ P

1

V

1

H

2

= H

1

proces izoentalpowy

William Thomson to późniejszy lord Kelvin.
Efekt J-T jest podstawą skraplania gazów metodą Lindego.
Przegroda porowata, to tzw. dławik.
Uwaga! Praca jest wykonywana na układzie, gaz bowiem jest
PRZETŁACZANY przez dławik.

23

Chem. Fiz. TCH II/05

23

Skraplanie gazów. Efekt

Joule’a-Thomsona (2).

Współczynnik Joule’a – Thomsona:

H

JT

P

T













∂

∂

=

µ

Można dowieść, że :









−











 ∂

=

V

dT

V

T

C

P

P

JT

1

µ

Dla gazu doskonałego (V=RT/P):

0

;

0

=

=

−











 ∂

JT

P

V

dT

V

T

µ

Dla każdego gazu rzeczywistego istnieje tzw. temperatura inwersji, T

inw

.

Gdy T < T

inw

,

µ

JT

>0

, gdy T > T

inw

,

µ

JT

<0

, gdy T = T

inw

,

µ

JT

=0

.

T

inw

zależy od ciśnienia (mogą być dwie T

inw

– dolna i górna).

Dowód proszę przeprowadzić sobie samemu, wychodząc z różniczki zupełnej
entalpii (względem ciśnienia i temperatury) oraz używając różniczki
dH=TdS+VdP, a także uwzględniając, że pochodna cząstkowa entropii po
ciśnieniu (w stałej T) jest równa pochodnej cząstkowej objętości po temperaturze
przy stałym ciśnieniu.
Przy okazji pytanie. Dlaczego proste rozprężanie adiabatyczne gazu doskonałego
prowadzi jednak do obniżenia jego temperatury?

24

Chem. Fiz. TCH II/05

24

Na każdy stopień swobody ruchu translacyjnego (na każdy człon
kwadratowy energii kinetycznej) cząsteczki przypada identyczna

energia równa ½kT

Zasada ekwipartycji energii

Prawidłowość ta jest spełniona tylko dla helu (i innych gazów

jednoatomowych).

Najwyraźniej, cząsteczki gazu posiadają jeszcze inną energię.

Gdyby, jak wynika z modelu kinetycznego, energia translacyjna była

jedyną energią cząsteczek gazu, to:

R

C

dT

du

V

V

2

3

=

=













a ze znanych względów

R

C

P

2

5

=

Ekwipartycja ( z łac. equipartitio) znaczy „równy podział”.
Trzy stopnie swobody ruchu translacyjnego, to ruch wzdłuż każdej z trzech osi
przestrzennych, x, y, z.

25

Chem. Fiz. TCH II/05

25

Cząsteczki mogą także wykonywać ruch rotacyjny (obrót wokół osi

symetrii). Dla cząsteczek dwuatomowych lub o budowie liniowej (2

osie, moment bezwładności wokół trzeciej – głównej osi cząsteczki

liniowej – jest pomijalny), istnieją dwa stopnie swobody rotacji, zatem

Pojemności cieplne gazów

(1)

gdzie J jest momentem bezwładności.

Dla cząsteczek przestrzennych, o trzech momentach bezwładności

RT

J

E

rot

=

=

2

2

1

ω

RT

E

rot

2

3

=

Niektóre lekkie gazy słabo wzbudzają się rotacyjnie w niskich temperaturach,
stąd wspomniane w wykładzie 4 odstępstwa od reguły Troutona.

26

Chem. Fiz. TCH II/05

26

Zatem, dla cząsteczek liniowych:

Pojemności cieplne gazów

(2)

Stwierdzono jednak, że w wysokich temperaturach, krzywa

ogrzewania gazów wieloatomowych wykazuje jeszcze większe

pojemności cieplne. Dochodzi wtedy do wzbudzenia oscylacyjnego.

a dla nieliniowych (przestrzennych):

R

C

V

2

5

=

R

C

P

2

7

=

R

C

V

3

=

R

C

P

4

=

Chodzi o krzywą T=f(H), pokazaną na wykładzie 4.

27

Chem. Fiz. TCH II/05

27

a na każde drganie przypadają dwa stopnie swobody (energia

potencjalna i kinetyczna). Zatem w wysokich temperaturach, dla

gazów dwuatomowych

Liczba drgań normalnych wynosi, dla cząsteczek :

nieliniowych liniowych

Pojemności cieplne gazów

(3)

Ogólnie, energia wewnętrzna gazów dana jest równaniem:

5

3

−

N

6

3

−

N

R

C

V

2

7

=

R

C

P

2

9

=

const

RT

RT

RT

E

E

E

E

U

nukl

el

osc

rot

tr

+

+

+

=

+

+

+

=

2

3

.

.,

Wzrost C

V

ponad wartość 5/2RT zachodzi nie skokowo, ale płynnie.

Energia elektronów i jąder atomowych nie zależy od temperatury, zatem nie
znajduje odbicia w pojemnościach cieplnych.

28

Chem. Fiz. TCH II/05

28

Ściśliwość gazów (1)

RT

PV

Z

m

=

0

=

dP

dZ

Współczynnik ściśliwości gazów dany jest wzorem:

Dla gazu doskonałego wynosi on zawsze 1 zaś pochodna:

'

lim

...

'

2

'

0

B

dP

dZ

C

B

dP

dZ

P

=

+

+

=

→

Dla gazów rzeczywistych:

Jednak B nie musi być równe zeru, ponadto zależy od temperatury.

Istnieje temperatura, zwana temperaturą Boyle’a, w której B = 0

dla P

→ 0, czyli gazy rzeczywiste zachowują się w niej naprawdę

jak gaz doskonały (w niskich ciśnieniach).

Z faktu, że Z jest dla gazów doskonałych równe 1 wynika, że jego wartość może
być miarą odchyleń od prawa Boyle’a.
To, że dla niższych ciśnień równanie wirialne przechodzi w równanie Clapeyrona
(pomijamy drugi i wyższe współczynniki wirialne) nie znaczy, że gazy
rzeczywiste stają się doskonałymi, a jedynie, że równanie Clapeyrona dobrze
opisuje ich zachowanie.

29

Chem. Fiz. TCH II/05

29

Powodem są oddziaływania międzycząsteczkowe odpychające

(bliskiego zasięgu) i przyciągające (dalszego zasięgu).

Ściśliwość gazów (2)

gaz doskonały

30

Chem. Fiz. TCH II/05

30

Lepkość gazów (1)

(1)

;

A

dx

dv

F

η

=

(2)

;

8

4

τ

η

π

l

∆P

r

v

=

Współczynnik tarcia wewnętrznego,

η

, czyli lepkość, możemy

rozpatrywać w kategoriach teorii kinetycznej gazów, jako wymianę pędu

przez cząsteczki sąsiadujących warstw poruszającego się gazu.

(tylko 1/3 wymienia pęd wzdłuż osi x); N=N

A

·

λ

A/V

m

λ

v

v+

λ

·dv/dx

Jedna cząsteczka przenosi pęd:

dx

dv

m

p

λ

=

1

Jeżeli w V=

λ

A

znajduje się N cząsteczek:

dx

dv

Nm

p

t

λ

3

1

=

dx

dv

A

p

t

2

3

1

ρλ

=

Równanie (1) jest równaniem definiującym lepkość, gdzie F jest siłą tarcia
między warstwami o powierzchni styku A, przy gradiencie szybkości w kierunku
normalnym do płaszczyzny warstw równym dv/dx.
Równanie (2) jest równaniem Poiseuille’a, gdzie r jest promieniem rurki
kapilarnej, l – jej długością,

∆

P – różnicą ciśnień między wylotem a wlotem,

τ

-

czasem wypływu, zaś v – objętością gazu jaka przepłynęła przez rurkę.
Na szkicu

λ

jest średnią drogą swobodną cząsteczek gazu.

Oś x jest tu osią pionową.
Ostatnie równanie zawiera gęstość,

ρ

, która jest równa m·N

A

/V

m

.

31

Chem. Fiz. TCH II/05

31

Lepkość gazów (2)

Porównując ostatnie równanie z r-niem Poiseuille’a:

Jeżeli wszystko dzieje się w czasie

τ

=1/z

:

τ

ρλ

1

2

3

1

dx

dv

A

F

=

a ponieważ

λ

/

τ

=ĉ

:

A

dx

dv

c

F

λ

ρ

3

1

=

c

ρλ

η

3

1

=

który to wynik możemy dowolnie komplikować podstawiając doń

wielkości uzyskane z rozkładu Maxwella.

Wnioski:

(sprawdzające się doświadczalnie)

• lepkość nie zależy od ciśnienia,

• lepkość zależy od pierwiastka kwadrato-

wego temperatury

Wzór Sutherlanda:

T

c

T

+

=

1

0

η

η

Odnośnie niektórych symboli – patrz slajd „Rozkład Maxwella (2)”.
We wzorze Sutherlanda (półempirycznym) stałe

η

0

i c są wielkościami

charakterystycznymi dla danej substancji.

32

Chem. Fiz. TCH II/05

32

Przewodnictwo cieplne

gazów

τ

χ

Ad

dx

dT

dq

=

V

V

c

c

c

η

λ

ρ

χ

=

=

3

1

Przepływ ciepła zależy od gradientu temperatury dT/dx. Ilość ciepła

przechodząca przez prostopadłą do gradientu temperatury

powierzchnię A, w czasie d

τ

wynosi:

Przewodnictwo cieplne gazu,

χ

, polega na przenoszeniu energii

kinetycznej przez cząsteczki pomiędzy sąsiadującymi warstwami.

Rozumując analogicznie jak w przypadku lepkości, otrzymujemy:

Przewodnictwo cieplne gazów jest niezmiernie ważne w

niektórych metodach detekcji gazów i par (np. w GC).

Wielkość c

V

jest ciepłem właściwym (pojemnością cieplną na gram) przy stałej

objętości.

33

Chem. Fiz. TCH II/05

33

Dyfuzja

τ

Ad

dx

dc

D

dm

=

c

D

λ

3

1

=

Dyfuzja zależy od gradientu stężeń dc/dx. Masa substancji

przechodząca przez prostopadłą do gradientu stężenia powierzchnię

A

, w czasie d

τ

wynosi (II prawo Ficka):

Współczynnik dyfuzji, D, jest charakterystyczny dla substancji i tem-

peratury. Rozumując analogicznie jak w poprzednich przypadkach, gdy

autodyfuzja polega na ruchu termicznym cząsteczek gazu, otrzymujemy:

34

Chem. Fiz. TCH II/05

34

Efuzja

π

ρ

π

ρ

µ

2

2

4

1

P

RT

M

P

c

=

=

=

πρ

2

P

v

=

Efuzja polega na wypływie gazu z naczynia pod ciśnieniem przez otwór

(lub otwory) o wielkości mniejszej od średniej drogi swobodnej.

Strumień masy gazu przechodzący przez takie otwory

(masa na 1 cm

2

na 1 sekundę) wynosi:

Efuzja ma ogromne znaczenie praktyczne. Opisuje przepływ przez

przegrody porowate (np. separacja izotopów).

Objętościowo zaś (cm

3

/(cm

2

s)):

Ostatni wzór to tzw. prawo Grahama, odkryte już doświadczalnie w 1829 roku.

35

Chem. Fiz. TCH II/05

35

Entalpia swobodna a

lotność gazów (1)

V

dP

G

T

=











 ∂

Z części termodynamicznej wykładu pamiętamy, że:

Dla izotermy zatem:

VdP

dG

=

oraz:

∫

=

−

2

1

1

2

P

P

VdP

G

G

1

2

1

2

ln

2

1

P

P

RT

P

dP

RT

G

G

P

P

=

=

−

∫

Dla gazu doskonałego:

Jeżeli P

1

= P

0

, a odpowiadającą mu G oznaczymy G

0

, to dla innego

ciśnienia P:

0

0

ln

P

P

RT

G

G

+

=

Równanie to spełnione jest dla gazów rzeczywistych jedynie

ze wszystkimi znanymi ograniczeniami.

Pierwsza pochodna cząstkowa jest wynikiem przekształcenia równania na
slajdzie „Podstawowe równania. Podsumowanie(3)”.

P

0

= 1 atm = 1,01325·10

5

Pa.

G

0

nazywamy standardową entalpią

swobodną.

36

Chem. Fiz. TCH II/05

36

Entalpia swobodna a

lotność gazów (2)

Definicja lotności (ciśnienia efektywnego):

0

0

ln

P

f

RT

G

G

+

=

P

f

φ

=

gdzie

φ

jest współczynnikiem lotności.

Stan standardowy gazu rzeczywistego jest hipotetycznym stanem, w

którym gaz znajdujący się pod ciśnieniem P

0

zachowuje się jak gaz

doskonały.

Ogólnie zatem:

φ

ln

ln

0

0

RT

P

P

RT

G

G

+

+

=

Można dowieść, że:

(

)

∫

−

=

P

P

dP

Z

0

1

ln

φ

a także:

...

'

'

ln

2

2

1

+

+

=

P

C

P

B

φ

Są uzasadnione powody, aby tak właśnie
zdefiniować stan standardowy.
Gdyby przyjąć, że w stanie
standardowym f = P

0

, to stany

standardowe różnych gazów byłyby
różne i skomplikowane.
Gdyby zaś założyć, że stan standardowy
odpowiada P = 0, to powstaje kłopot,
gdyż G

→

-

∞

, gdy P

→

0.

Związek Z z równaniem wirialnym –
patrz slajd „Ściśliwość gazów (1)”.
Można także obliczać lotność
korzystając z równania Van der Waalsa.

37

Chem. Fiz. TCH II/05

37

Potencjał chemiczny

mieszanin gazowych (1)

i

n

T

i

V

dP

i

=











 ∂

,

µ

Dla mieszanin obowiązuje analogicznie:

Jeżeli mieszanina spełnia prawo Daltona:

i

i

dP

V

d

=

µ

i

i

i

P

RT

n

V

=

Dla mieszaniny gazów doskonałych:

a zatem:

i

n

T

P

i

i

i

P

RT

n

V

V

i

j

=













∂

∂

=

≠

,

,

oraz

i

i

i

P

dP

RT

d

=

µ

Ostatecznie:

0

0

ln

P

P

RT

i

i

i

+

=

µ

µ

Gdzie

µ

i

0

jest standardowym potencjałem chemicznym składnika i

(odpowiadającemu jego ciśnieniu równemu standardowemu).

38

Chem. Fiz. TCH II/05

38

Potencjał chemiczny

mieszanin gazowych (2)

Uprzednie równania spełniane są przez gazy rzeczywiste ze

wszystkimi znanymi ograniczeniami.

Musimy więc stosować lotności.

'

"

'

"

ln

i

i

i

i

f

f

RT

µ

µ

−

=

Oznaczając przez

µ

i

0

potencjał chemiczny składnika i

w stanie standardowym

0

0

ln

P

f

RT

i

i

i

+

=

µ

µ

Używamy dla stanów oznaczeń ’ i ”
ponieważ oznaczenia cyfrowe
zarezerwowane są dla składników.