•1

Chem. Fiz. TCH II/05

1

Podstawowe równania –

podsumowanie (1)

Ts

u

f

−

=

w

q

u

+

=

dw

dq

du

+

=

sdT

Tds

du

df

−

−

=

dq

ds

=

T

:

go

odwracalne

procesu

dla

sdT

dq

du

df

−

−

=

:

zatem

dw

dq

du

=

−

:

go)

odwracalne

procesu

(dla

kolei

z

a

sdT

dw

df

−

=

:

wtedy

a

( )

0

:

na

izochorycz

jest

przemiana

jednak

gdy

=

T,V

df

PdV

dw

−

=

( )

dw

df

T

=

:

izotermy

dla

a

To wszystko jest prawdziwe, gdy w układzie nie występuje praca

nie objętościowa!!!

( )

dw

df

dq

Tds

T

<

>

i

:

lnego

nieodwraca

procesu

dla

a

( )

0

:

oraz

<

T,V

df

Chem. Fiz. TCH II/05

2

Podstawowe równania –

podsumowanie (2)

Ts

h

g

−

=

PV

u

h

+

=

VdP

PdV

du

dh

+

+

=

sdT

Tds

dh

dg

−

−

=

dq

ds

=

T

:

go

odwracalne

procesu

dla

sdT

VdP

PdV

dw

dg

−

+

+

=

:

zatem

dw

dq

du

=

−

:

i

( )

0

:

ej

izobaryczn

przemiany

dla

,

=

+

=

PdV

dw

dg

P

T

PdV

dw

−

=

:

ponadto

a

( )

VdP

PdV

dw

dg

T

+

+

=

:

izotermy

dla

Prawdziwe, gdy w układzie nie występuje praca nie objętościowa!!!

( )

VdP

PdV

dw

dg

dq

Tds

T

+

+

<

>

i

:

lnego

nieodwraca

procesu

dla

a

( )

0

:

oraz

<

T,P

dg

sdT

Tds

VdP

PdV

du

dg

−

−

+

+

=

Chem. Fiz. TCH II/05

3

Podstawowe równania –

podsumowanie (3)

(odwr.)

dw

Tds

du

+

=

PdV

Tds

du

−

=

obj.

tylko

praca

gdy

a

Pole powyżej zawiera podstawowe równania termodynamiki.

Ts

h

g

−

=

PV

u

h

+

=

dq

dw

du

+

=

(odwr.)

q

Tds

=

Ts

u

f

−

=

VdP

PdV

du

dh

+

+

=

:

zatem

VdP

Tds

dh

+

=

:

i

sdT

Tds

du

df

−

−

=

:

podobnie

PdV

sdT

df

−

−

=

:

i

sdT

Tds

dh

dg

−

−

=

:

raz

jeszcze

VdP

sdT

dg

+

−

=

:

i

s

T

f

V

−

=













∂

∂

P

V

f

T

−

=













∂

∂

s

T

g

P

−

=













∂

∂

V

P

g

T

=













∂

∂

•2

Chem. Fiz. TCH II/05

4

Termodynamika układów

otwartych

W układach otwartych, tzn. wymieniających z otoczeniem także

materię, zmienia się ich skład.

Jeśli zawierają one więcej niż jeden, maksymalnie zaś k składników, to
dowolna funkcja stanu musi zależeć od parametrów stanu układu i jego

składu.

)

,...

,...

,

,

,

(

2

1

k

i

n

n

n

n

T

P

f

y

=

W konsekwencji:

i

n

P

T

i

n

P

T

n

T

n

P

dn

dn

dy

dn

dn

dy

dP

dP

dy

dT

dT

dy

dy

i

j

j

i

i

≠

≠













+













+













+













=

,

,

1

,

,

1

,

,

1

Chem. Fiz. TCH II/05

5

Cząstkowe molowe

wielkości (1)

Wielkości określone pochodną:

i

j

n

P

T

i

dn

dy

≠













,

,

nazywamy cząstkowymi molowymi wielkościami:

i

j

n

P

T

i

i

dn

dy

Y

≠













=

,

,

za pomocą których możemy opisać zmiany stanu układu otwartego:

k

k

i

i

n

T

n

P

dn

Y

dn

Y

dn

Y

dP

dP

dy

dT

dT

dy

dy

i

i

+

+

+

+

+













+













=

...

...

1

1

,

,

W szczególności, w warunkach

izotermiczno-izobarycznych:

∑

=

=

k

i

i

i

dn

Y

dy

1

Chem. Fiz. TCH II/05

6

Cząstkowe molowe

wielkości (2)

Można ją więc scałkować (po dowolnej drodze) od stanu

n

i

=0 do stanu n

i

(końcowe). Droga ta może być taka, aby:

const

Y

i

=

_

W tych warunkach:

∑

=

k

i

i

i

dn

Y

1

jest różniczką zupełną funkcji y

ergo

, funkcją stanu układu, zależną od jego składu.

W wyniku czego otrzymujemy:

∑

=

=

k

i

i

i

Y

n

y

1

∑

∑

=

=

+

=

k

i

i

i

k

i

i

i

dn

Y

Y

d

n

dy

1

1

zaś najogólniejsze wyrażenie na jej

różniczkę zupełną dane jest równaniem:

•3

Chem. Fiz. TCH II/05

7

Równanie Gibbsa-Duhema

Ostatnie wyrażenie nosi nazwę równania Gibbsa-Duhema.

Jeśli:

∑

∑

=

=

+

=

k

i

i

i

k

i

i

i

dn

Y

Y

d

n

dy

1

1

a równocześnie:

∑

=

=

k

i

i

i

dn

Y

dy

1

_

ergo

, musi być prawdziwe:

0

1

=

∑

=

k

i

i

i

Y

d

n

Dla układu dwuskładnikowego, można je wyrazić:

0

2

2

1

1

=

+

Y

d

n

Y

d

n

0

2

2

1

1

=

+

Y

d

x

Y

d

x

lub:

gdzie:

2

1

2

2

2

1

1

1

;

n

n

n

x

n

n

n

x

+

=

+

=

są ułamkami molowymi
składników 1 i 2.

Chem. Fiz. TCH II/05

8

Cząstkowe molowe

wielkości (3)

Najczęściej stosowane cząstkowe molowe wielkości to:

cząstkowa molowa entalpia:

i

j

n

P

T

i

i

n

h

H

≠













∂

∂

=

,

,

cząstkowa molowa entropia:

i

j

n

P

T

i

i

n

s

S

≠













∂

∂

=

,

,

cząstkowa molowa objętość:

i

j

n

P

T

i

i

n

v

V

≠













∂

∂

=

,

,

i najważniejsza z nich, cząstkowa molowa entalpia swobodna,

zwana też potencjałem chemicznym:

i

j

n

P

T

i

i

i

n

g

G

≠













∂

∂

=

=

,

,

µ

Chem. Fiz. TCH II/05

9

Cząstkowe molowe

wielkości (4)

Zależności pomiędzy cząstkowymi molowymi wielkościami są

analogiczne do zachodzących pomiędzy h, s, v i g.

Np., różniczkując względem n

i

wyrażenie:

Ts

h

g

−

=

otrzymujemy:

=

−

=

=

∂

∂

−

∂

∂

=

∂

∂

i

i

i

i

i

i

S

T

H

n

s

T

n

h

n

g

µ

a wychodząc z zależności:

s

T

g

P

−

=













∂

∂

otrzymamy:

S

T

n

s

n

T

g

i

i

i

−

=

∂

∂

=

∂

∂

−

=

∂

∂

∂

µ

2

•4

Chem. Fiz. TCH II/05

10

Cząstkowe molowe

wielkości (5)

Najważniejsza zależność termodynamiki chemicznej:

k

k

i

i

dn

dn

dn

SdT

VdP

dG

µ

µ

µ

+

+

+

+

+

−

=

...

...

1

1

Pod stałym ciśnieniem i w stałej temperaturze:

k

k

i

i

dn

dn

dn

dG

µ

µ

µ

+

+

+

+

=

...

...

1

1

A wtedy, praca nieobjętościowa może być spowodowana zmianą

składu chemicznego układu. Np. w ogniwie galwanicznym zmiana

jego składu chemicznego (od substratów do produktów) prowadzi

do uzyskania pracy elektrycznej.

Chem. Fiz. TCH II/05

11

Gazy

Zagadnienia omawiane w tej części, przynajmniej w

pewnym zakresie, traktuję jako powtórkę.

Niektóre przeźrocza w tej serii są zatem jedynie

materiałem pomocniczym!

Większość omawianych tutaj zagadnień można

(i należy) powtórzyć sobie z dowolnego podręcznika

chemii fizycznej lub fizyki.

Chem. Fiz. TCH II/05

12

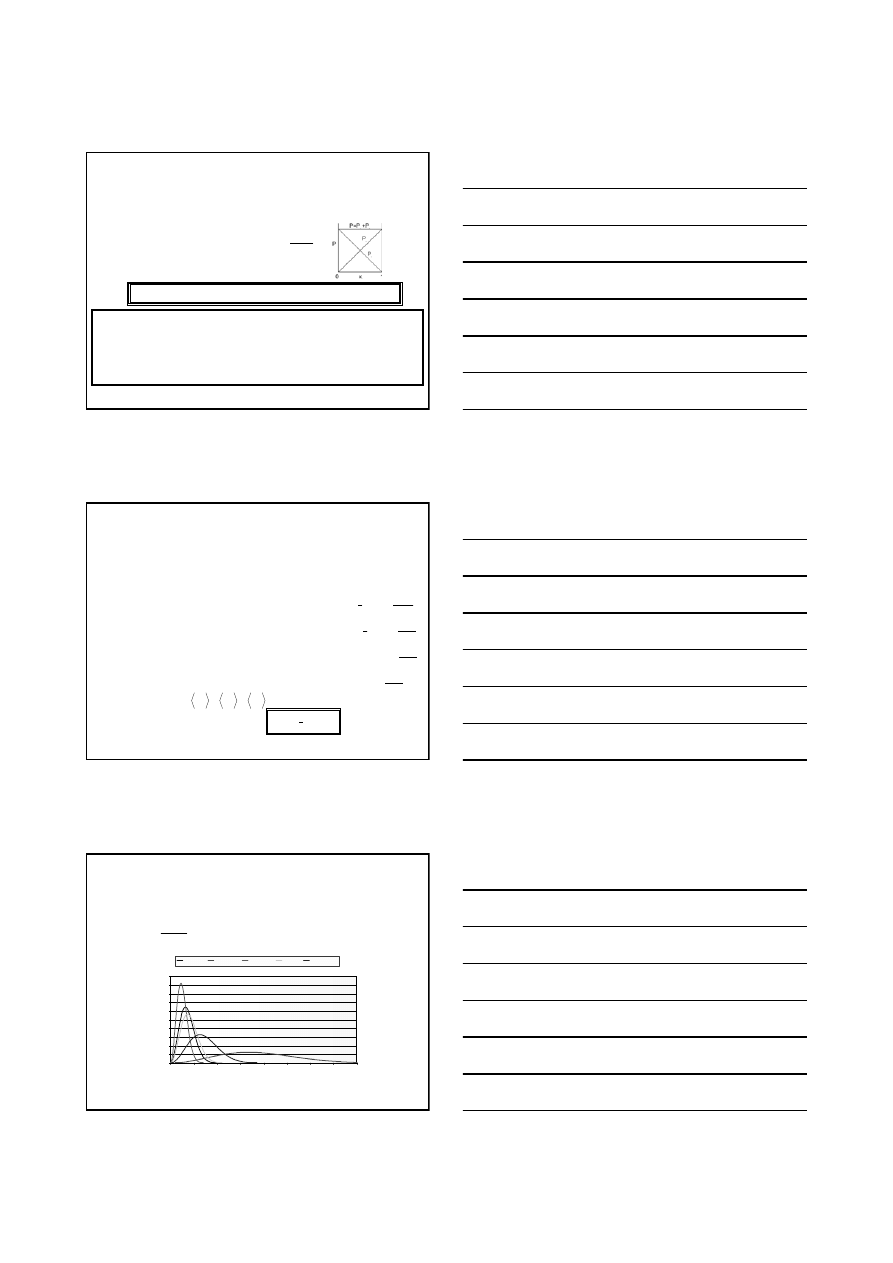
Gaz doskonały(1).

Prawa gazowe

Boyle’a

izoterma

const

T

const

PV

=

=

dla

;

Charlesa

izobara

const

P

T

V

=

∝

dla

;

Gay-Lussaca

izochora

const

V

T

P

=

∝

dla

;

Równanie Clapeyrona

nRT

PV

=

T

PV

R

m

P 0

lim

→

=

•5

Chem. Fiz. TCH II/05

13

Gaz doskonały(2).

Prawa gazowe, c.d.

Avogadro

n

const

V

⋅

=

Daltona

;

;

1

i

i

k

i

i

x

P

P

P

P

⋅

=

=

∑

=

∑

=

=

k

i

i

i

i

n

n

x

1

Założenia kinetycznego modelu gazu doskonałego:

•

Cząsteczki gazu, o masie m znajdują się w ciągłym, chaotycznym

ruchu.

•

Jedyne oddziaływanie pomiędzy cząsteczkami, jak również

między nimi a ścianką zbiornika to zderzenia idealnie sprężyste.

•

Rozmiary cząsteczek są pomijalnie małe w porównaniu ze średnią

drogą pomiędzy zderzeniami (średnią drogą swobodną).

Chem. Fiz. TCH II/05

14

Gaz doskonały(3).

Ciśnienie wg modelu kinetycznego

1

2

mv

mv

t

F

−

=

∆

Druga zasada dynamiki Newtona:

V

nN

t

Av

l

A

x

∆

=

2

1

Liczba cząsteczek uderzających w ściankę o pow.

A

w czasie

∆

t

(zmiana szybkości z mv

x

na – mv

x

):

Ich masa (masa jednej cząsteczki to M/N

A

) :

Ich całkowita zmiana pędu :

V

nM

t

Av

lm

x

∆

=

2

1

V

nM

t

Av

t

F

x

∆

=

∆

2

Wywierane ciśnienie (F/A) :

V

nM

v

P

x

2

=

Ponieważ :

2

2

2

2

z

y

x

v

v

v

c

+

+

=

To ostatecznie :

nM

c

PV

2

3

1

=

Chem. Fiz. TCH II/05

15

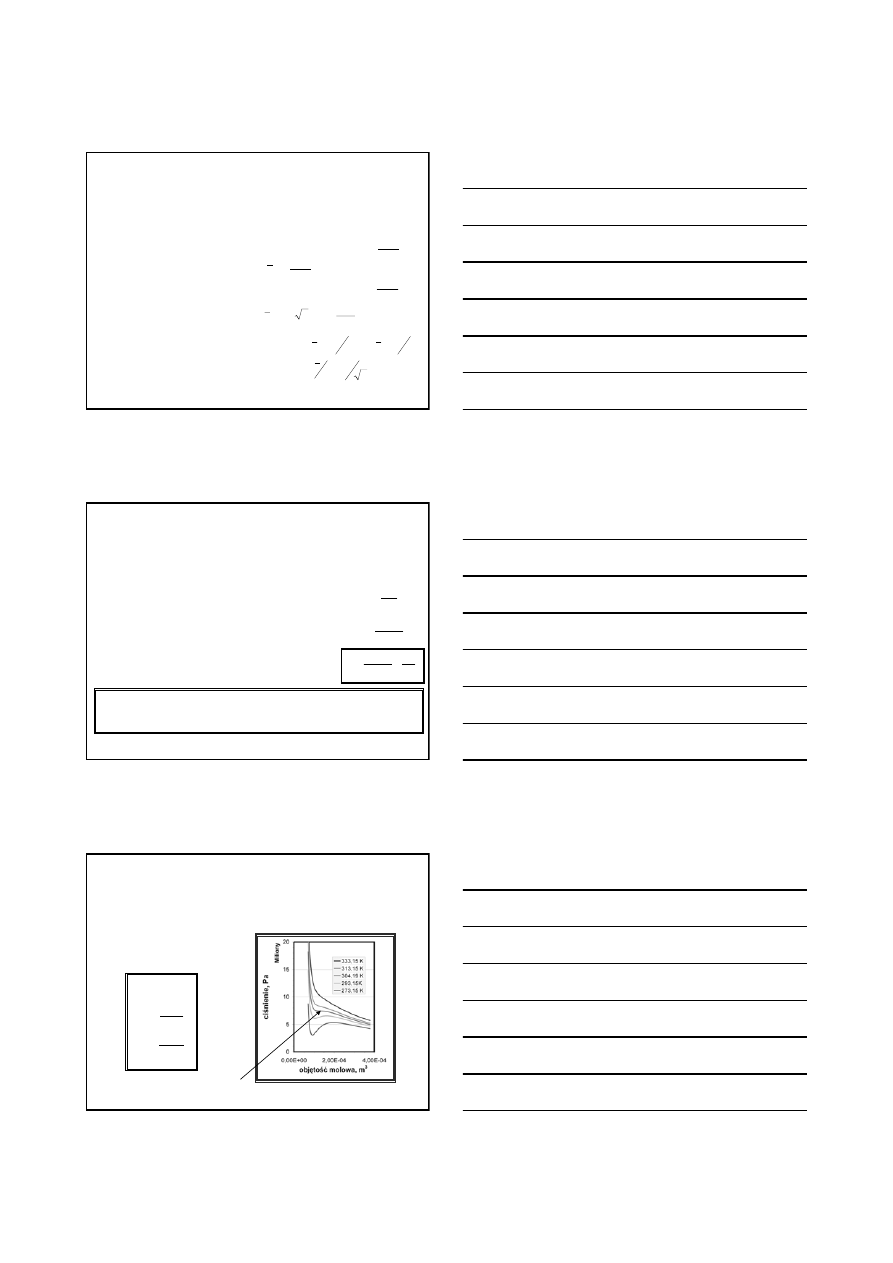
Rozkład Maxwella (1)

0

0,02

0,04

0,06

0,08

0,1

0,12

0,14

0,16

0,18

0,2

0

10

20

30

40

50

60

70

80

s zybkoś ć , m/s

wz

g

lę

dna

l

ic

z

b

a

c

z

ą

st

e

c

z

e

k

He ; 10 K

He ; 273 K

Rn; 273 K

Kr; 273

Azot;273 K

)

2

/(

2

2

/

3

2

2

4

)

(

RT

Mv

e

v

RT

M

v

f

−













=

π

π

bez wyprowadzania

•6

Chem. Fiz. TCH II/05

16

Rozkład Maxwella (2)

2

/

1

3













=

M

RT

c

Wykorzystując rozkład Maxwella można także wyznaczyć

takie własności cząsteczek gazu jak:

szybkość średnia kwadratowa :

szybkość średnia :

szybkość najbardziej prawdopodobna:

średnia szybkość względna:

częstość zderzeń:

średnia droga swobodna:

2

/

1

8













=

M

RT

c

π

2

/

1

2

*













=

M

RT

c

2

/

1

8

2













=

⋅

=

πµ

kT

c

c

wzgl

kT

P

c

V

N

c

z

wzgl

wzgl

⋅

=

⋅

=

σ

σ

P

kT

z

c

σ

λ

2

=

=

Chem. Fiz. TCH II/05

17

Gazy rzeczywiste. Równanie

stanu Van der Waalsa

nRT

PV

=

Udoskonalenie (urealnienie) równania Clapeyrona:

na 1 mol gazu:

Poprawka na objętość mola cząsteczek gazu, b

m

V

RT

P

=

b

V

RT

P

m

−

=

Poprawka na oddziaływania międzycząsteczkowe, a

2

m

m

V

a

b

V

RT

P

−

−

=

• same cząsteczki gazu zajmują pewną objętość, b

• atraktywne (przyciągające) oddziaływania międzycząsteczkowe zmniejszają pęd

(zatem siłę) cząsteczek zmierzających ku ściance, a także częstość ich zderzeń ze

ścianką, dodatkowo zmniejszają więc ciśnienie (do kwadratu stężenia cząsteczek).

Chem. Fiz. TCH II/05

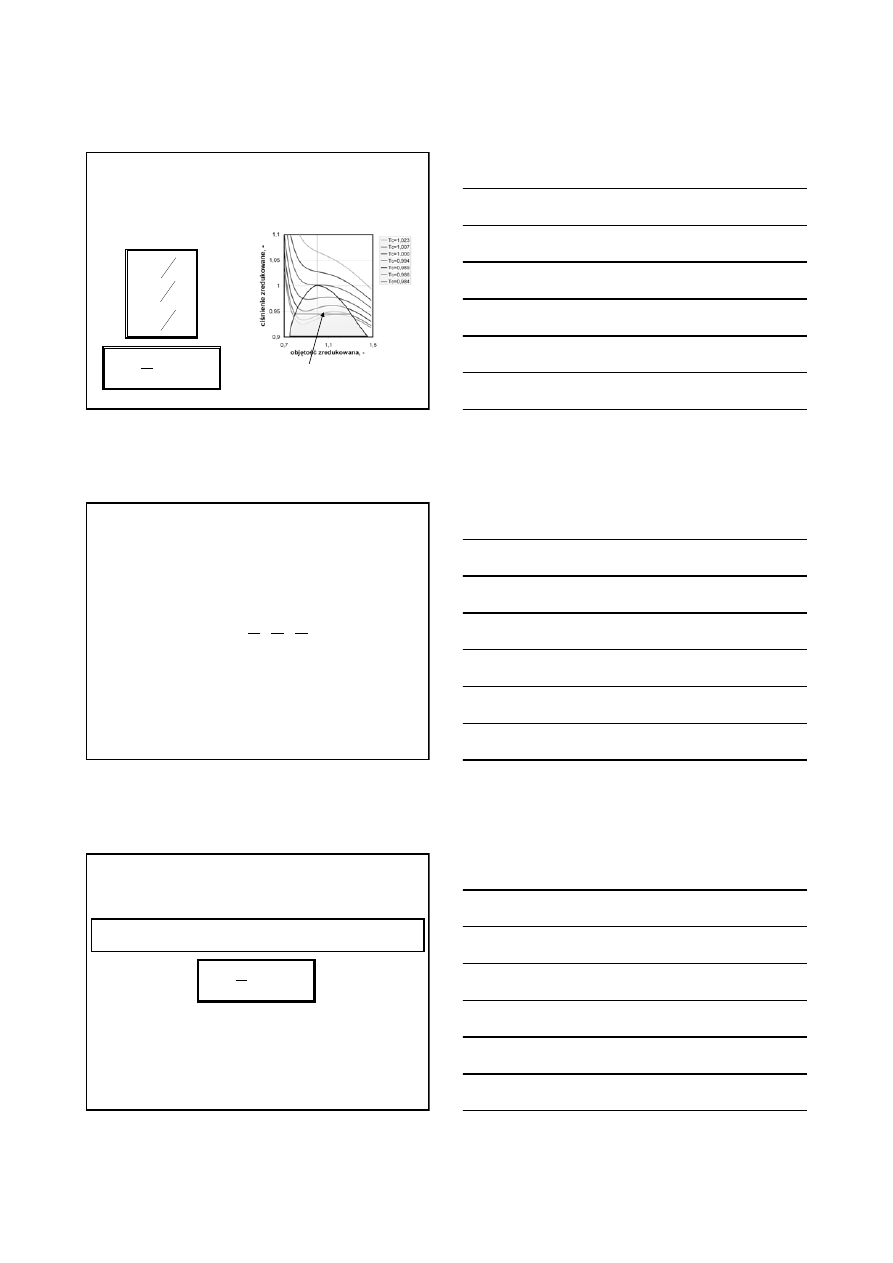
18

Izotermy Van der Waalsa

(1)

punkt krytyczny

b

V

c

3

=

2

27b

a

P

c

=

bR

a

T

c

27

8

=

Związki między

współczynnikami r-nia Van

der Waalsa a parametrami

krytycznymi:

•7

Chem. Fiz. TCH II/05

19

Izotermy Van der Waalsa

(2)

c

P

P

=

π

c

V

V

=

φ

c

T

T

=

θ

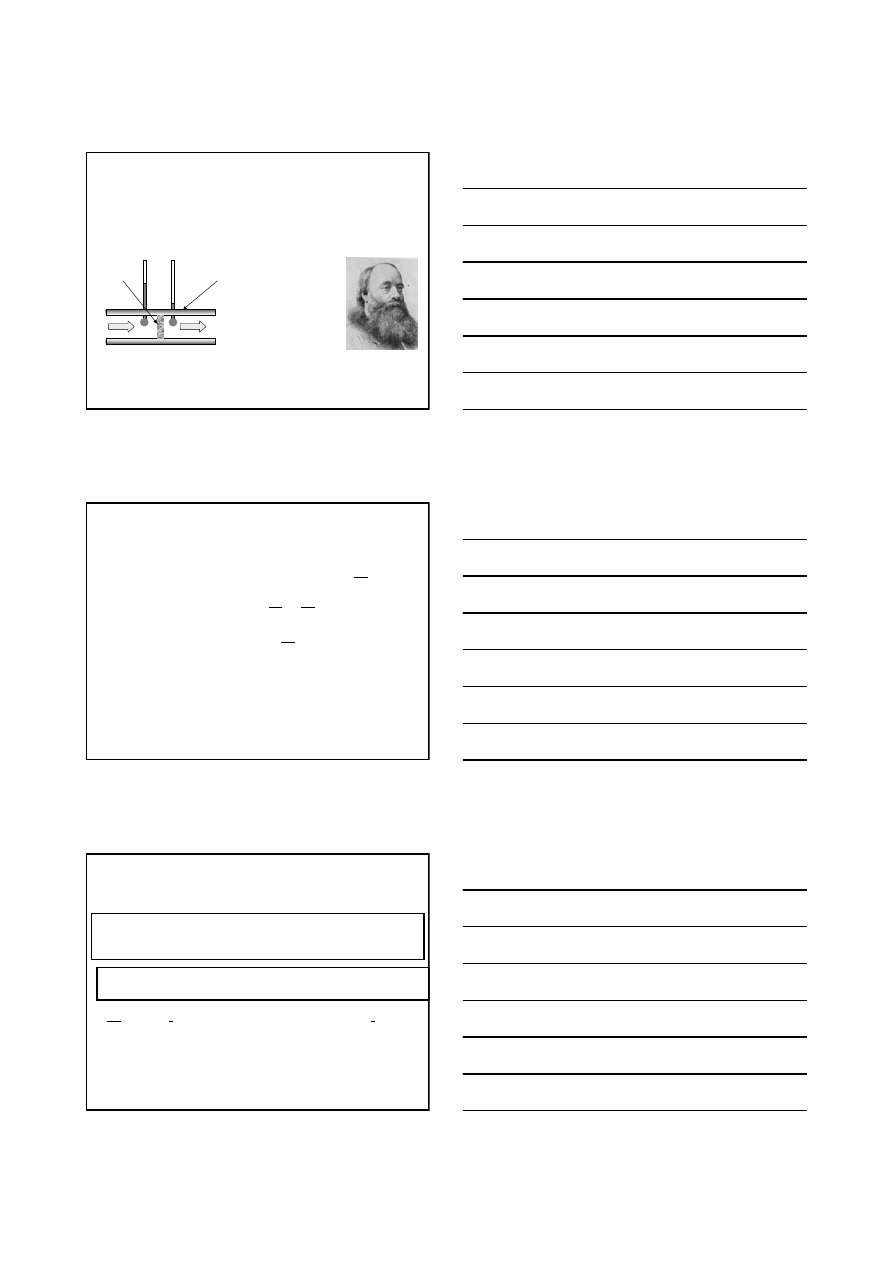
rzeczywisty przebieg

izotermy podczas skraplania

zredukowane parametry stanu

i równanie Van der Waalsa

(

)

θ

φ

φ

π

8

1

3

3

2

=

−











 +

Chem. Fiz. TCH II/05

20

Wirialne równania stanu

...)

'

'

'

1

(

3

2

+

+

+

+

=

P

D

P

C

P

B

RT

PV

m













+

+

+

+

=

...

1

3

2

m

m

m

m

V

D

V

C

V

B

RT

PV

Zaproponował je Kamerlingh Onnes (dwie formy):

Współczynniki B, C, D (B’, C’, D’) noszą nazwę

współczynników wirialnych (zależą od temperatury).

Często stosuje się jedynie drugi współczynnik wirialny:

P

B

RT

PV

m

"

+

=

Chem. Fiz. TCH II/05

21

Gazy rzeczywiste w tych samych warunkach zredukowanej objętości

i temperatury wywierają takie samo ciśnienie zredukowane.

Zasada stanów

odpowiadających sobie

Wynika ze zredukowanego r-nia Van der Waalsa (znikają w nim

bowiem charakterystyczne dla poszczególnych gazów współczynniki

a

i b). Inne równania stanu też ją zawierają.

Zasada ta zawodzi, gdy cząsteczki gazu są nie sferyczne lub polarne.

(

)

θ

φ

φ

π

8

1

3

3

2

=

−











 +

•8

Chem. Fiz. TCH II/05

22

Skraplanie gazów. Efekt

Joule’a-Thomsona (1).

Klasyczne metody sprężania poniżej w temperaturze T<T

c

często nie

wystarczały do skroplenia gazów o coraz niższych T

c

.

q = 0

adiabatyczne

rozprężanie

-w = P

2

V

2

– P

1

V

1

James Joule

rura izolowana

termicznie

przegroda

porowata

P

1

,T

1

P

2

,T

2

U

2

– U

1

= P

2

V

2

– P

1

V

1

U

2

+ P

2

V

2

= U

1

+ P

1

V

1

H

2

= H

1

proces izoentalpowy

Chem. Fiz. TCH II/05

23

Skraplanie gazów. Efekt

Joule’a-Thomsona (2).

Współczynnik Joule’a – Thomsona:

H

JT

P

T













∂

∂

=

µ

Można dowieść, że :









−











 ∂

=

V

dT

V

T

C

P

P

JT

1

µ

Dla gazu doskonałego (V=RT/P):

0

;

0

=

=

−











 ∂

JT

P

V

dT

V

T

µ

Dla każdego gazu rzeczywistego istnieje tzw. temperatura inwersji, T

inw

.

Gdy T < T

inw

,

µ

JT

>0

, gdy T > T

inw

,

µ

JT

<0

, gdy T = T

inw

,

µ

JT

=0

.

T

inw

zależy od ciśnienia (mogą być dwie T

inw

– dolna i górna).

Chem. Fiz. TCH II/05

24

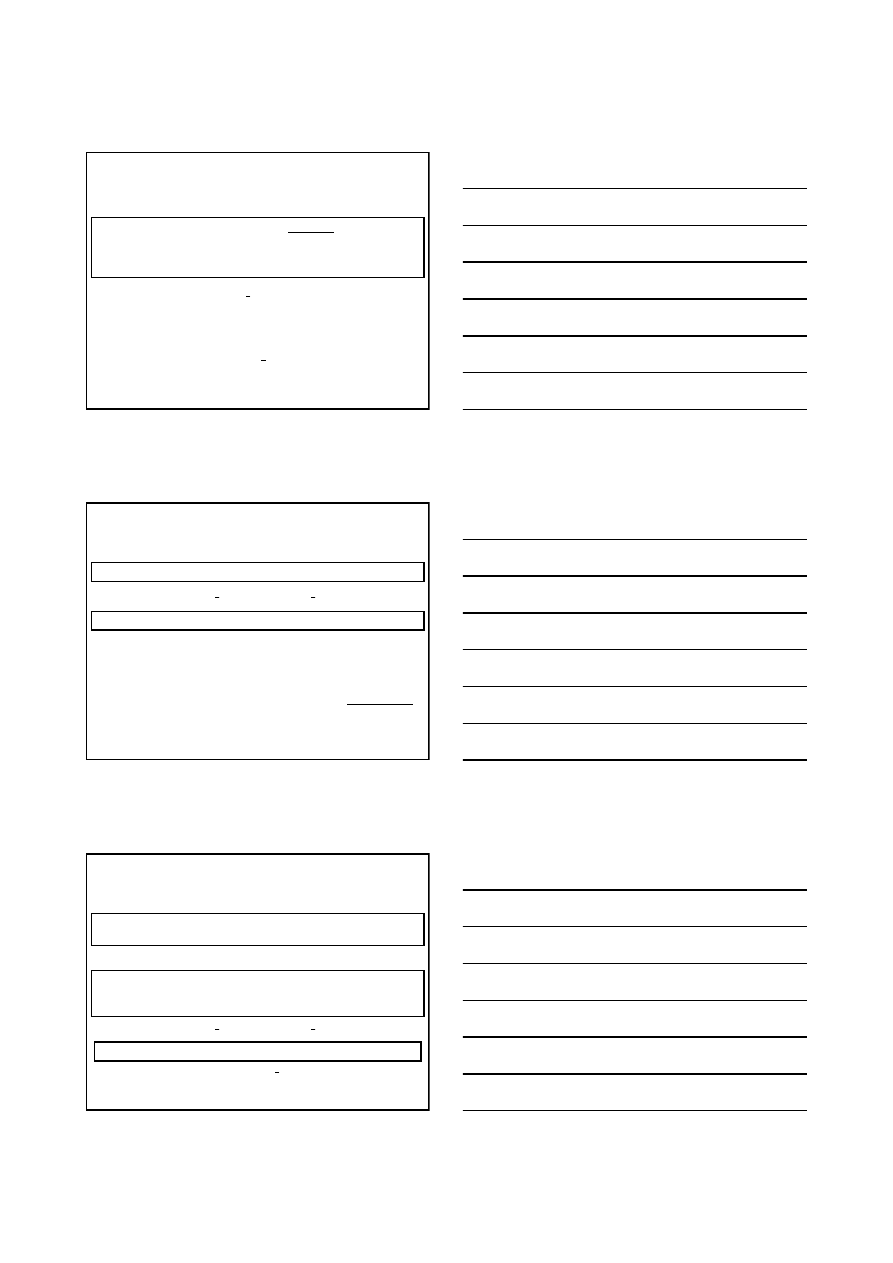
Na każdy stopień swobody ruchu translacyjnego (na każdy człon
kwadratowy energii kinetycznej) cząsteczki przypada identyczna

energia równa ½kT

Zasada ekwipartycji energii

Prawidłowość ta jest spełniona tylko dla helu (i innych gazów

jednoatomowych).

Najwyraźniej, cząsteczki gazu posiadają jeszcze inną energię.

Gdyby, jak wynika z modelu kinetycznego, energia translacyjna była

jedyną energią cząsteczek gazu, to:

R

C

dT

du

V

V

2

3

=

=













a ze znanych względów

R

C

P

2

5

=

•9

Chem. Fiz. TCH II/05

25

Cząsteczki mogą także wykonywać ruch rotacyjny (obrót wokół osi

symetrii). Dla cząsteczek dwuatomowych lub o budowie liniowej (2

osie, moment bezwładności wokół trzeciej – głównej osi cząsteczki

liniowej – jest pomijalny), istnieją dwa stopnie swobody rotacji, zatem

Pojemności cieplne gazów

(1)

gdzie J jest momentem bezwładności.

Dla cząsteczek przestrzennych, o trzech momentach bezwładności

RT

J

E

rot

=

=

2

2

1

ω

RT

E

rot

2

3

=

Chem. Fiz. TCH II/05

26

Zatem, dla cząsteczek liniowych:

Pojemności cieplne gazów

(2)

Stwierdzono jednak, że w wysokich temperaturach, krzywa

ogrzewania gazów wieloatomowych wykazuje jeszcze większe

pojemności cieplne. Dochodzi wtedy do wzbudzenia oscylacyjnego.

a dla nieliniowych (przestrzennych):

R

C

V

2

5

=

R

C

P

2

7

=

R

C

V

3

=

R

C

P

4

=

Chem. Fiz. TCH II/05

27

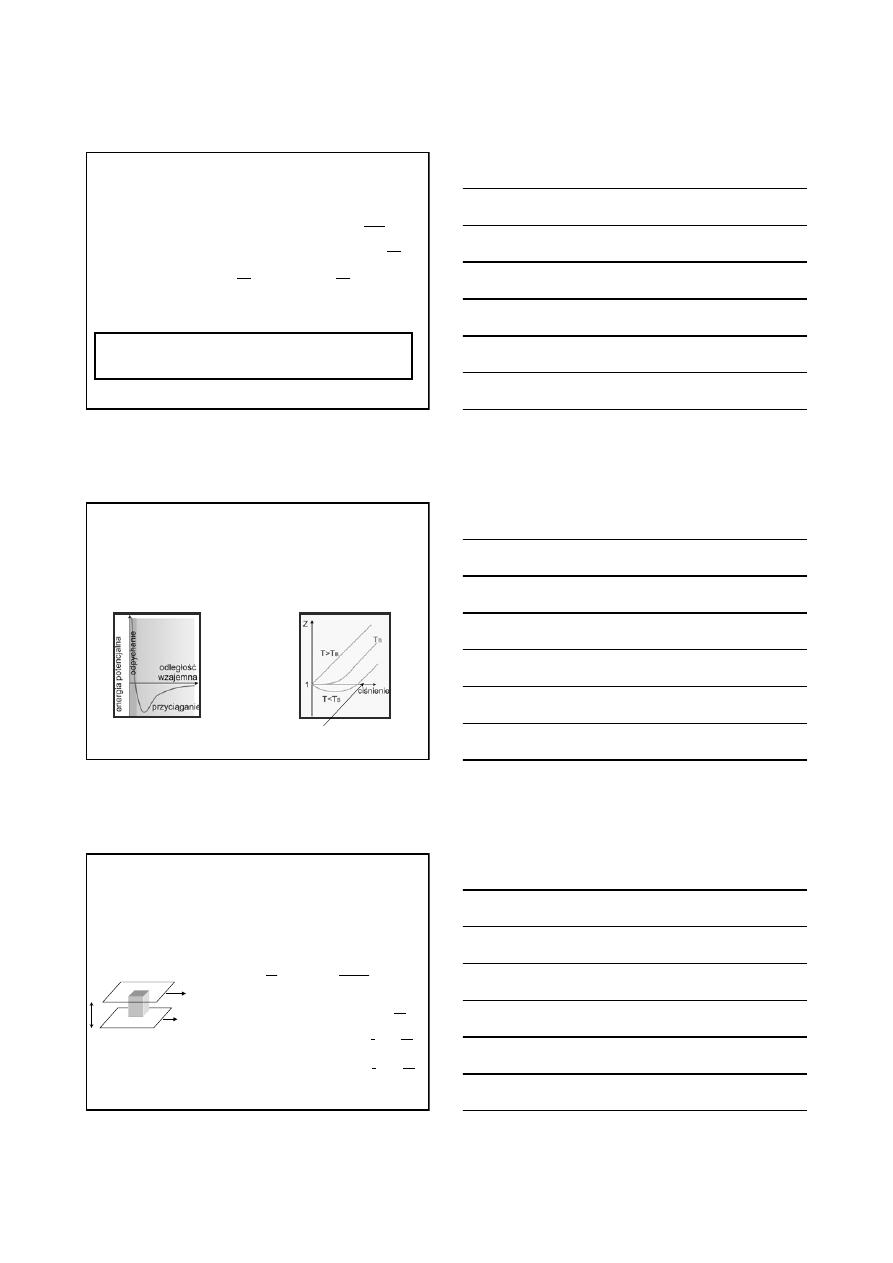
a na każde drganie przypadają dwa stopnie swobody (energia

potencjalna i kinetyczna). Zatem w wysokich temperaturach, dla

gazów dwuatomowych

Liczba drgań normalnych wynosi, dla cząsteczek :

nieliniowych liniowych

Pojemności cieplne gazów

(3)

Ogólnie, energia wewnętrzna gazów dana jest równaniem:

5

3

−

N

6

3

−

N

R

C

V

2

7

=

R

C

P

2

9

=

const

RT

RT

RT

E

E

E

E

U

nukl

el

osc

rot

tr

+

+

+

=

+

+

+

=

2

3

.

.,

•10

Chem. Fiz. TCH II/05

28

Ściśliwość gazów (1)

RT

PV

Z

m

=

0

=

dP

dZ

Współczynnik ściśliwości gazów dany jest wzorem:

Dla gazu doskonałego wynosi on zawsze 1 zaś pochodna:

'

lim

...

'

2

'

0

B

dP

dZ

C

B

dP

dZ

P

=

+

+

=

→

Dla gazów rzeczywistych:

Jednak B nie musi być równe zeru, ponadto zależy od temperatury.

Istnieje temperatura, zwana temperaturą Boyle’a, w której B = 0

dla P

→ 0, czyli gazy rzeczywiste zachowują się w niej naprawdę

jak gaz doskonały (w niskich ciśnieniach).

Chem. Fiz. TCH II/05

29

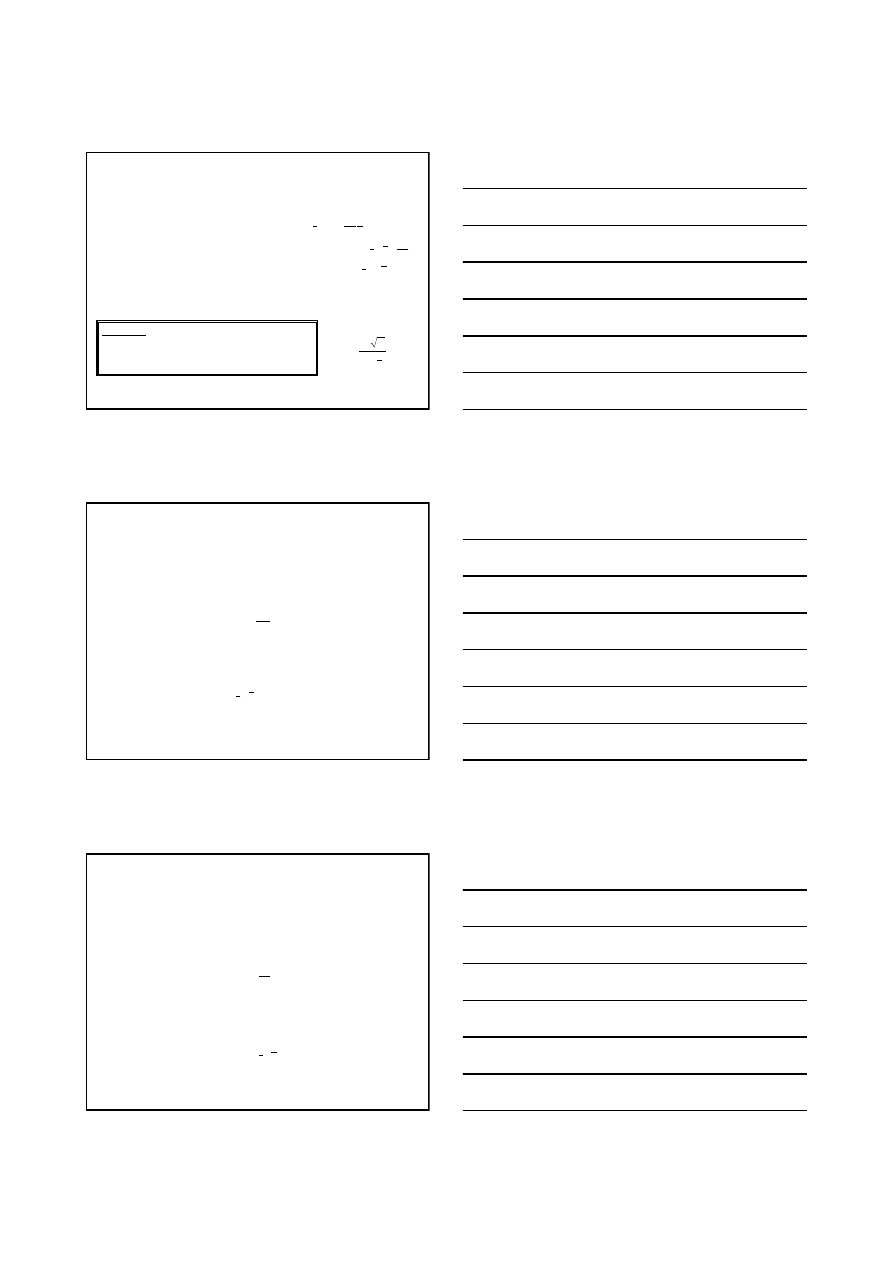
Powodem są oddziaływania międzycząsteczkowe odpychające

(bliskiego zasięgu) i przyciągające (dalszego zasięgu).

Ściśliwość gazów (2)

gaz doskonały

Chem. Fiz. TCH II/05

30

Lepkość gazów (1)

(1)

;

A

dx

dv

F

η

=

(2)

;

8

4

τ

η

π

l

∆P

r

v

=

Współczynnik tarcia wewnętrznego,

η

, czyli lepkość, możemy

rozpatrywać w kategoriach teorii kinetycznej gazów, jako wymianę pędu

przez cząsteczki sąsiadujących warstw poruszającego się gazu.

(tylko 1/3 wymienia pęd wzdłuż osi x); N=N

A

·

λ

A/V

m

λ

v

v+

λ

·dv/dx

Jedna cząsteczka przenosi pęd:

dx

dv

m

p

λ

=

1

Jeżeli w V=

λ

A

znajduje się N cząsteczek:

dx

dv

Nm

p

t

λ

3

1

=

dx

dv

A

p

t

2

3

1

ρλ

=

•11

Chem. Fiz. TCH II/05

31

Lepkość gazów (2)

Porównując ostatnie równanie z r-niem Poiseuille’a:

Jeżeli wszystko dzieje się w czasie

τ

=1/z

:

τ

ρλ

1

2

3

1

dx

dv

A

F

=

a ponieważ

λ

/

τ

=ĉ

:

A

dx

dv

c

F

λ

ρ

3

1

=

c

ρλ

η

3

1

=

który to wynik możemy dowolnie komplikować podstawiając doń

wielkości uzyskane z rozkładu Maxwella.

Wnioski:

(sprawdzające się doświadczalnie)

• lepkość nie zależy od ciśnienia,

• lepkość zależy od pierwiastka kwadrato-

wego temperatury

Wzór Sutherlanda:

T

c

T

+

=

1

0

η

η

Chem. Fiz. TCH II/05

32

Przewodnictwo cieplne

gazów

τ

χ

Ad

dx

dT

dq

=

V

V

c

c

c

η

λ

ρ

χ

=

=

3

1

Przepływ ciepła zależy od gradientu temperatury dT/dx. Ilość ciepła

przechodząca przez prostopadłą do gradientu temperatury

powierzchnię A, w czasie d

τ

wynosi:

Przewodnictwo cieplne gazu,

χ

, polega na przenoszeniu energii

kinetycznej przez cząsteczki pomiędzy sąsiadującymi warstwami.

Rozumując analogicznie jak w przypadku lepkości, otrzymujemy:

Przewodnictwo cieplne gazów jest niezmiernie ważne w

niektórych metodach detekcji gazów i par (np. w GC).

Chem. Fiz. TCH II/05

33

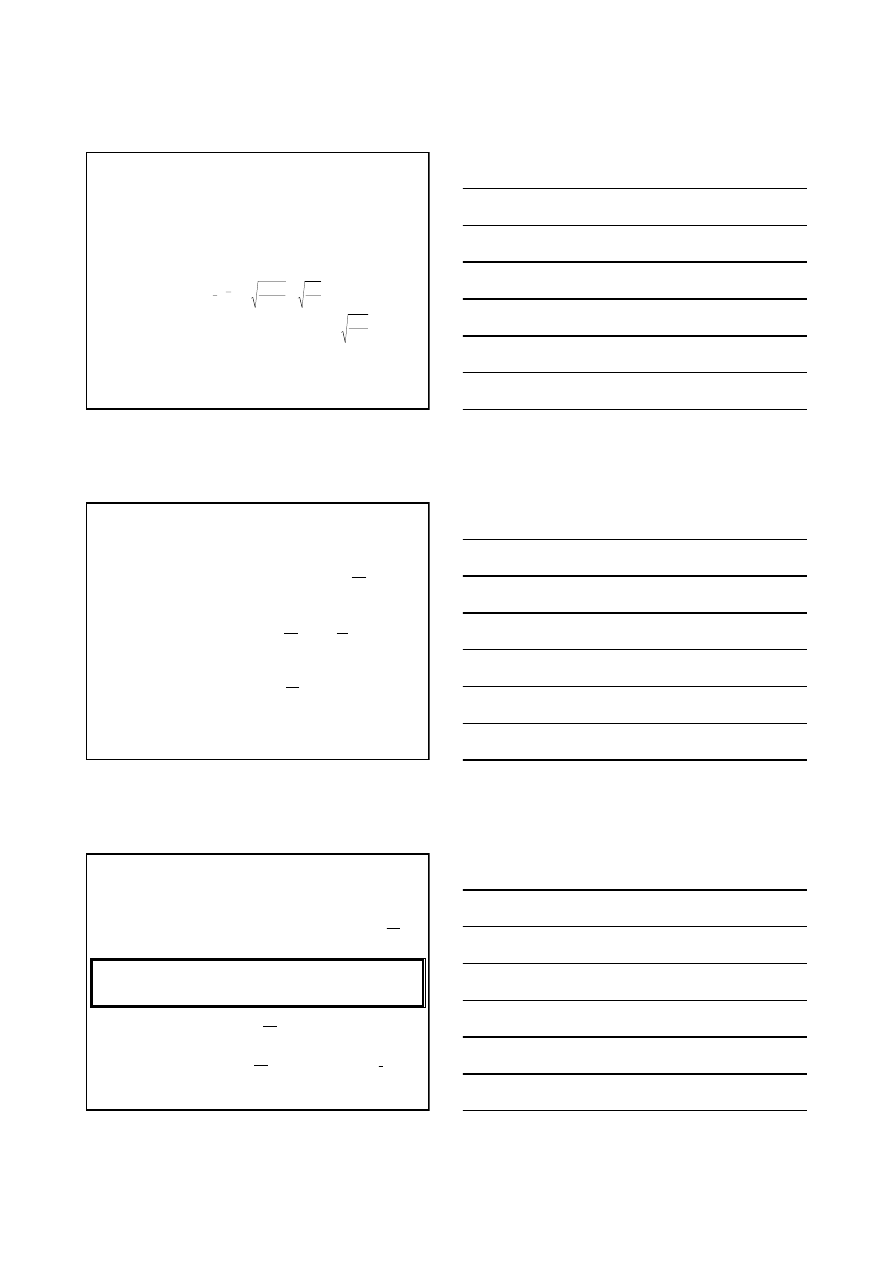
Dyfuzja

τ

Ad

dx

dc

D

dm

=

c

D

λ

3

1

=

Dyfuzja zależy od gradientu stężeń dc/dx. Masa substancji

przechodząca przez prostopadłą do gradientu stężenia powierzchnię

A

, w czasie d

τ

wynosi (II prawo Ficka):

Współczynnik dyfuzji, D, jest charakterystyczny dla substancji i tem-

peratury. Rozumując analogicznie jak w poprzednich przypadkach, gdy

autodyfuzja polega na ruchu termicznym cząsteczek gazu, otrzymujemy:

•12

Chem. Fiz. TCH II/05

34

Efuzja

π

ρ

π

ρ

µ

2

2

4

1

P

RT

M

P

c

=

=

=

πρ

2

P

v

=

Efuzja polega na wypływie gazu z naczynia pod ciśnieniem przez otwór

(lub otwory) o wielkości mniejszej od średniej drogi swobodnej.

Strumień masy gazu przechodzący przez takie otwory

(masa na 1 cm

2

na 1 sekundę) wynosi:

Efuzja ma ogromne znaczenie praktyczne. Opisuje przepływ przez

przegrody porowate (np. separacja izotopów).

Objętościowo zaś (cm

3

/(cm

2

s)):

Chem. Fiz. TCH II/05

35

Entalpia swobodna a

lotność gazów (1)

V

dP

G

T

=











 ∂

Z części termodynamicznej wykładu pamiętamy, że:

Dla izotermy zatem:

VdP

dG

=

oraz:

∫

=

−

2

1

1

2

P

P

VdP

G

G

1

2

1

2

ln

2

1

P

P

RT

P

dP

RT

G

G

P

P

=

=

−

∫

Dla gazu doskonałego:

Jeżeli P

1

= P

0

, a odpowiadającą mu G oznaczymy G

0

, to dla innego

ciśnienia P:

0

0

ln

P

P

RT

G

G

+

=

Równanie to spełnione jest dla gazów rzeczywistych jedynie

ze wszystkimi znanymi ograniczeniami.

Chem. Fiz. TCH II/05

36

Entalpia swobodna a

lotność gazów (2)

Definicja lotności (ciśnienia efektywnego):

0

0

ln

P

f

RT

G

G

+

=

P

f

φ

=

gdzie

φ

jest współczynnikiem lotności.

Stan standardowy gazu rzeczywistego jest hipotetycznym stanem, w

którym gaz znajdujący się pod ciśnieniem P

0

zachowuje się jak gaz

doskonały.

Ogólnie zatem:

φ

ln

ln

0

0

RT

P

P

RT

G

G

+

+

=

Można dowieść, że:

(

)

∫

−

=

P

P

dP

Z

0

1

ln

φ

a także:

...

'

'

ln

2

2

1

+

+

=

P

C

P

B

φ

•13

Chem. Fiz. TCH II/05

37

Potencjał chemiczny

mieszanin gazowych (1)

i

n

T

i

V

dP

i

=











 ∂

,

µ

Dla mieszanin obowiązuje analogicznie:

Jeżeli mieszanina spełnia prawo Daltona:

i

i

dP

V

d

=

µ

i

i

i

P

RT

n

V

=

Dla mieszaniny gazów doskonałych:

a zatem:

i

n

T

P

i

i

i

P

RT

n

V

V

i

j

=













∂

∂

=

≠

,

,

oraz

i

i

i

P

dP

RT

d

=

µ

Ostatecznie:

0

0

ln

P

P

RT

i

i

i

+

=

µ

µ

Gdzie

µ

i

0

jest standardowym potencjałem chemicznym składnika i

(odpowiadającemu jego ciśnieniu równemu standardowemu).

Chem. Fiz. TCH II/05

38

Potencjał chemiczny

mieszanin gazowych (2)

Uprzednie równania spełniane są przez gazy rzeczywiste ze

wszystkimi znanymi ograniczeniami.

Musimy więc stosować lotności.

'

"

'

"

ln

i

i

i

i

f

f

RT

µ

µ

−

=

Oznaczając przez

µ

i

0

potencjał chemiczny składnika i

w stanie standardowym

0

0

ln

P

f

RT

i

i

i

+

=

µ

µ