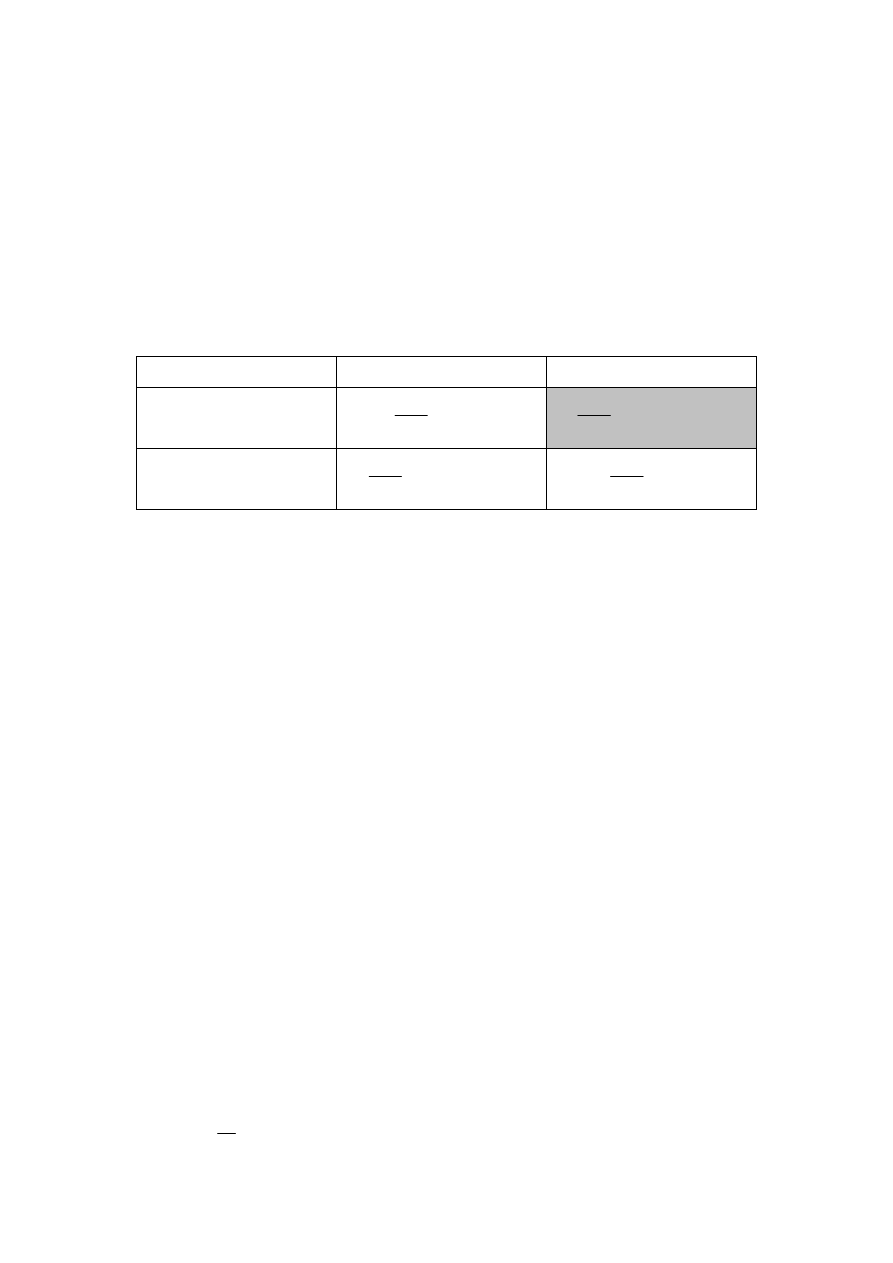
Przykład 1: Oblicz odsetki proste według stopy r=10% od kapitału

początkowego 1000 zł w czasie od 5 marca 2006 do 17 sierpnia 2006 w każdym

z czterech wariantów rachunku czasu.

165

17

31

30

31

30

)

5

31

(

t

K

=

+

+

+

+

+

−

=

64

229

−

=

162

17

30

4

)

5

30

(

t

B

=

+

⋅

+

−

=

Lata kalendarzowe n

K

Lata bankowe n

B

Dokładna liczba dni t

K

365

165

=0,452

360

165

=0,458 (max)

Bankowa liczba dni t

B

365

162

=0,444 (min)

360

162

=0,45

(t

K

, n

K

):

45,2

452

,

0

1

,

0

1000

n

r

P

I

=

⋅

⋅

=

⋅

⋅

=

(t

K

, n

B

):

45,8

458

,

0

1

,

0

1000

n

r

P

I

=

⋅

⋅

=

⋅

⋅

=

(t

B

, n

K

):

44,4

444

,

0

1

,

0

1000

n

r

P

I

=

⋅

⋅

=

⋅

⋅

=

(t

B

, n

B

):

45,0

45

,

0

1

,

0

1000

n

r

P

I

=

⋅

⋅

=

⋅

⋅

=

Praca domowa: zadania 1.1 - 1.7, 1.10 - 1.16, 1.18 – 1.20

Praca domowa na plusa do zwrotu na kartce: zadanie 1.8

Przykład 1: Bank A proponuje 15-miesięczną pożyczkę z odsetkami prostymi

płatnymi z dołu naliczanymi przy stopie r=7%. Bank B proponuje 15-

miesięczną pożyczkę z odsetkami prostymi płatnymi z góry naliczanymi przy

stopie d=7%. Która pożyczka jest korzystniejsza dla pożyczkobiorcy, który chce

otrzymać kwotę P=2000 zł?

P=2000,

25

,

1

n

12

15

=

=

2

A:

r=7% ⇒

175

25

,

1

07

,

0

2000

n

r

P

I

=

⋅

⋅

=

⋅

⋅

=

B:

d=7% ⇒

78

,

191

25

,

1

07

,

0

n

d

n

d

F

D

25

,

1

07

,

0

1

2000

n

d

1

P

H

=

⋅

⋅

=

⋅

⋅

=

⋅

⋅

=

⋅

−

⋅

−

Przykład 2: Opłata za 6-miesięczny kredyt spłacony kwotą 10 tys. zł ma postać

dyskonta handlowego prostego obliczonego przy stopie d równoważnej stopie

r=12,75% w okresie 6 miesięcy. Ile wynosi ta opłata?

F=10 000, r=12,75%,

5

,

0

n

12

6

=

=

%

99

,

11

5

,

0

0,1275

1

0,1275

n

r

1

r

d

=

⋅

+

=

⋅

+

=

, D

H

= F

⋅

d

⋅

n = 10 000

⋅

0,1199

⋅

0,5=599,29

9400,71

599,29

000

10

D

F

P

H

=

−

=

−

=

D

H

= I = P

⋅

r

⋅

n = F

⋅

(1+r

⋅

n)

-1

⋅

r

⋅

n =

29

,

599

5

,

0

1275

,

0

5

,

0

1275

,

0

1

10000

=

⋅

⋅

⋅

+

Przykład 3: Zobowiązanie do zapłaty za dostawę towaru o wartości 45 600 zł

ma postać weksla o terminie wykupu za 60 dni na sumę 46 600 zł. a) Na

zastosowanie jakiej stopy d zgodziły się strony transakcji? b) Przy jakiej rocznej

stopie procentowej r pożyczka z odsetkami prostymi płatnymi z dołu byłaby

równie korzystna jak podpisanie weksla?

600

46

F

=

,

600

45

P

=

,

6

1

360

60

n

=

=

a)

1000

600

45

600

46

P

F

D

H

=

−

=

−

=

D

H

= F

⋅

d

⋅

n,

1000 = 46 600

⋅

d

⋅

6

1

⇒

%

88

,

12

d

600

46

6

1000

=

=

⋅

b)

H

D

n

r

P

I

=

⋅

⋅

=

,

1000

r

600

45

6

1

=

⋅

⋅

⇒

%

16

,

13

r

600

45

6

1000

=

=

⋅

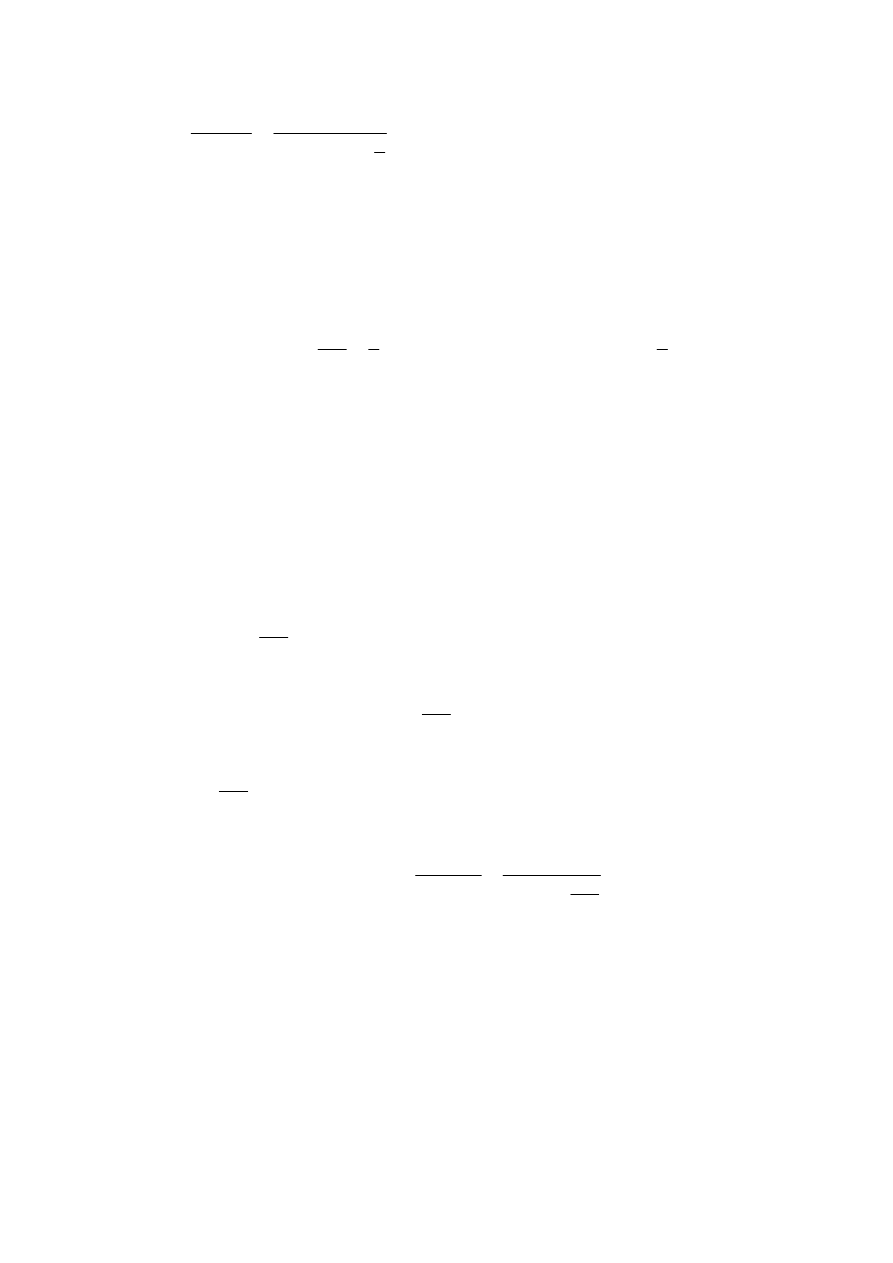
3

%

16

,

13

12,88%

1

12,88%

n

d

1

d

r

6

1

=

⋅

−

=

⋅

−

=

Przykład 4: Weksel z przykładu 3 został po 20 dniach od jego wystawienia

zdyskontowany w banku przy stopie d=13%. Jaką kwotę bank wypłacił

posiadaczowi weksla?

600

46

F

=

, d=13%,

9

1

360

40

n

=

=

, P = F

⋅

(1-d

⋅

n) = 46 600

⋅

(1-0,13

⋅

9

1

) = 45 926,89

Przykład 5: Wystawca weksla z przykładów 3-4 przewidując trudności ze spłatą

weksla o wartości nominalnej 46 600 w wymaganym terminie, zwraca się na 20

dni przed jego wykupem do banku, który przyjął weksel do dyskonta o jego

zamianę na weksel równoważny z terminem wykupu późniejszym o 30 dni. Jaka

jest wartość nominalna odnowionego weksla, jeśli w banku obowiązuje stopa

d=13%?

600

46

F

1

=

,

360

20

1

n

=

,

%

13

d

=

44

,

263

46

)

0,13

-

(1

600

46

)

n

d

(1

F

P

360

20

1

1

1

=

⋅

⋅

=

⋅

−

⋅

=

?

F

2

=

,

360

50

2

n

=

,

%

13

d

=

)

n

d

(1

F

P

P

2

2

2

1

⋅

−

⋅

=

=

⇒

11

,

47114

0,13

-

1

263,44

46

n

d

-

1

P

F

360

50

2

1

2

=

⋅

=

⋅

=

Praca domowa: zadania 2.1 – 2.5, 2.7 – 2.12