Twierdzenie sinusów
W dowolnym trójkącie stosunki długości boków do sinusów kątów przeciwległych są stałe i równe długości średnicy okręgu opisanego na tym trójkącie
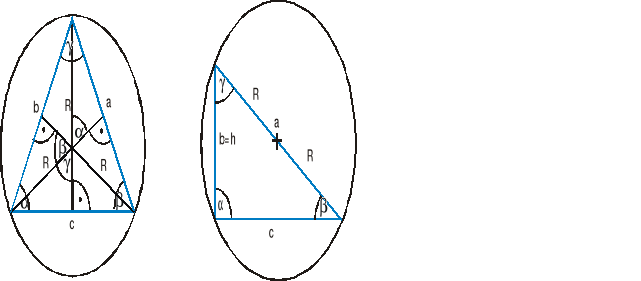
Założenie: Kąty α, β, γ leżą naprzeciw boków odpowiednio a, b, c
Teza: ![]()
![]()
Dowód:
We wszystkich tych trójkątach zachodzą związki:
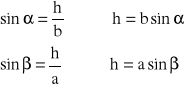
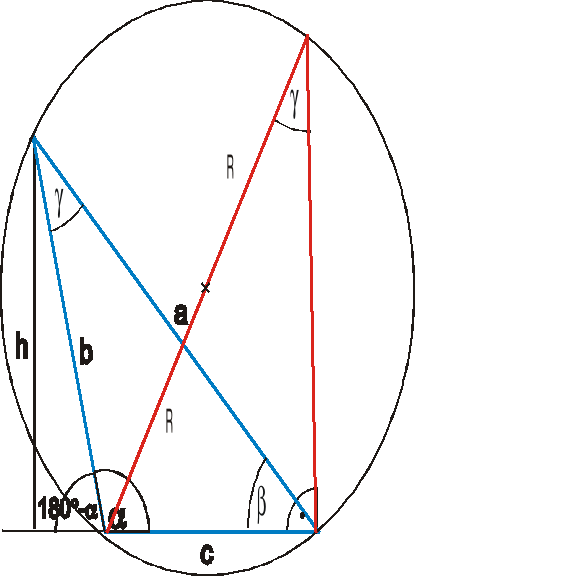
UWAGA! Dla trójkąta rozwartokątnego ![]()
![]()
Ponieważ lewe strony zależności są równe to prawe też więc: ![]()
![]()
przekształcając ostatnią równość otrzymujemy:
![]()
Trzeci człon dowodzimy analogicznie opuszczając wysokość z innego wierzchołka trójkąta.
Zachodzi jeszcze równość:
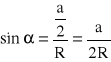
sin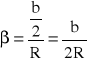
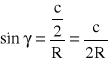
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
TwierdzeniecosinuswTMnr2, materialy, Matematyka, matematyka - dowody
TwierdzeniePitagorasa, materialy, Matematyka, matematyka - dowody
ftryg, materialy, Matematyka, matematyka - dowody
TM36, materialy, Matematyka, matematyka - dowody
tm29, materialy, Matematyka, matematyka - dowody
zadanie6, materialy, Matematyka, matematyka - dowody
tm16, materialy, Matematyka, matematyka - dowody
tm4-2, materialy, Matematyka, matematyka - dowody
tm3, materialy, Matematyka, matematyka - dowody
zadanie18, materialy, Matematyka, matematyka - dowody
tm35ciagi, materialy, Matematyka, matematyka - dowody
Iloczynkartezjaski, materialy, Matematyka, matematyka - dowody
tm5, materialy, Matematyka, matematyka - dowody
PROSTA, materialy, Matematyka, matematyka - dowody
tm4, materialy, Matematyka, matematyka - dowody
tm2Twierdzeniecosinusw, materialy, Matematyka, matematyka - dowody
TM31Wartbezwzgl, materialy, Matematyka, matematyka - dowody
kombinatorykaTM41, materialy, Matematyka, matematyka - dowody
ZadanieTM20, materialy, Matematyka, matematyka - dowody
więcej podobnych podstron