Z zależności (7.35) oraz (7.39) jest:
![]()
gdyż w rozpatrywanym przepływie prędkość krytyczna gazu pozostaje niezmienna. Podstawiając do (7.88) bezwymiarową prędkość λ w miejsce M oraz V mamy
![]()
(7.90)
i następnie całkując obustronnie to równanie w granicach od ![]()
do ![]()
otrzymujemy
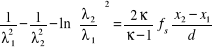
. (7.91)
Po wprowadzeniu zredukowanej długości przewodu
![]()
uzyskamy ostatecznie równanie
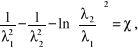
(7.92)
pozwalające określić bezwymiarową prędkość w przekroju ![]()
rury, dla zadanych wartości i χ .
ĆWICZENIA
Przykład 7.1. Obliczyć prędkość dźwięku, liczbę Macha oraz współczynnik prędkości dla strumienia powietrza wypływającego ze zbiornika z prędkością równą połowie maksymalnej prędkości wypływu. Temperatura w zbiorniku wynosi 150°C.
Najpierw obliczamy:
![]()
![]()
![]()
Prędkość wypływu jest równa
![]()
Z równania energii
mamy
![]()
Liczba Macha
Współczynnik prędkości
Przykład 7.2. Porównać prędkość wypływu powietrza ze zbiornika (w chwili początkowej), którą można otrzymać przy prawidłowym rozprężeniu powietrza do ciśnienia atmosferycznego: - w przypadku, gdy w zbiorniku ![]()
a ![]()
![]()
V2 - w przypadku izochorycznego podgrzania powietrza znajdującego się w zbiorniku do ![]()
V3 - w przypadku izobarycznego podgrzania powietrza znajdującego się w zbiorniku do tej samej temperatury. Przyjąć wysokość ciśnienia atmosferycznego równą h = 750 mm Hg.
W celu wyprowadzenia wzoru na prędkość wylotową korzysta się z równania energii (7.27), po wstawieniu do niego odpowiedniej wartości stałej (7.31)
![]()
skąd
![]()
Po wstawieniu zależności 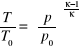
otrzymujemy wzór
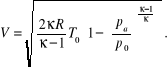
Wyznaczamy parametry gazu:
![]()
![]()
![]()
Obliczamy prędkości wypływu powietrza:
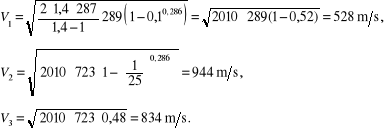
Przykład 7.3. Wraz ze wzrostem prędkości przepływu gazu maleje jego temperatura, a wraz z nią prędkość dźwięku może zmaleć do zera. Obliczyć, jaka będzie w tym przypadku liczba Macha oraz jaki będzie współczynnik prędkości.
Z równania energii wynika, że prędkość przepływu równa się w tym przypadku prędkości maksymalnej
![]()
Z definicji liczby Macha
Natomiast współczynnik prędkości
czyli
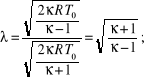
dla jest
Przykład 7.4. Przez kanał naddźwiękowy (rys. 7.14) o przekroju najwęższym równym przepływa izentropowo powietrze, którego krytyczne wielkości wynoszą i .
a. Obliczyć masowe natężenie przepływu w kanale.
b. Wyznaczyć liczbę Macha w kanale, przy której temperatura powietrza nie przekroczy temperatury
c. Wyznaczyć stosunek przekrojów ![]()
odpowiadający obliczonej liczbie Macha.
a. Masowe natężenie przepływu wynosi
![]()
192
Wyszukiwarka
Podobne podstrony:
ROZDZ7B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ7A, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ7E, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ0, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ8C, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ9C, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ8D, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ11A, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ5A, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ5B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ5C, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ10B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ4B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ8B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ3A, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ12B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ2B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ11B, Zbigniew Kosma Podstawy Mechaniki Płynów
ROZDZ2A, Zbigniew Kosma Podstawy Mechaniki Płynów
więcej podobnych podstron