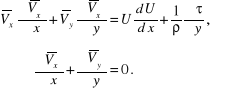
(10.49)

Dzięki dokonanym uproszczeniom trzeba do niego dołączyć tylko jedną zależność dodatkową dla naprężenia turbulentnego
Ponadto równania te mają postać identyczną z równaniami Prandtla, toteż ich zerowy moment jest identyczny co do formy ze związkiem całkowym Karmana (9.43).

*

Zbadamy teraz strukturę turbulentnej warstwy przyściennej dla przyjmując, że oś x pokrywa się ze ścianką oraz że przepływ nie zależy od zmien-
nej x, tzn.:

(10.50)

Przy tych założeniach układ (10.49) redukuje się do równania

z którego wynika, że

(10.51)

gdzie oznacza naprężenie na ściance; na mocy (10.38), (10.41) i (10.48) mamy więc

(10.52)

W związku z tym, że składnik reprezentujący naprężenie turbulentne jest mały w pobliżu ścianki - i odwrotnie - w dużej odległości od ścianki turbulencja jest w pełni rozwinięta i naprężenia laminarne są małe w porównaniu z turbulentnymi, nasuwa się koncepcja rozbicia równania (10.52) na dwa prostsze równania asymptotyczne. Pierwsze z nich

(10.53)

opisywać będzie ruch cieczy w pobliżu ścianki, drugie zaś

(10.54)

w dużej odległości od ścianki.

Obszar, w którym obowiązuje równanie (10.53) nazywamy podwarstwą laminarną natomiast obszar, w którym ruchem cieczy rządzi równanie (10.54) - rdzeniem turbulentnym . Pomiędzy tymi obszarami znajduje się obszar pośredni (przejściowy), w którym naprężenia laminarne i turbulentne są tego sa-mego rzędu.

Pomijając istnienie obszaru przejściowego „zszyjemy” rozwiązanie równania (10.53) z rozwiązaniem równania (10.54). Z równania (10.52) i warunku brzegowego (9.5) wynika, że rozkład prędkości w podwarstwie laminarnej jest liniowy

(10.55)

Zakładając dodatkowo

(10.56)

z równania (10.54) mamy

(10.57)

Po jego scałkowaniu otrzymamy rozkład prędkości w rdzeniu turbulentnym

(10.58)

w którym symbol oznacza prędkość dynamiczną

Stałą C wyznaczymy z warunku, aby prawe strony (10.55) i (10.58) były sobie rów-ne dla pewnego y = δ

(10.59)

Wprowadzając ponadto skalę długości

(10.60)

oraz zmienne bezwymiarowe:

(10.61)

uzyskujemy ostatecznie, jako wynik rozwiązania rozpatrywanego zagadnienia, dwie funkcje postaci:

(10.62)

(10.63)

Wartości liczbowe stałych κ oraz α muszą być zaczerpnięte z odpowiednich doświadczeń. Otrzymane rozwiązanie dla:

(10.64)

oraz wyniki badań eksperymentalnych zostały przedstawione na rys. 10.4.

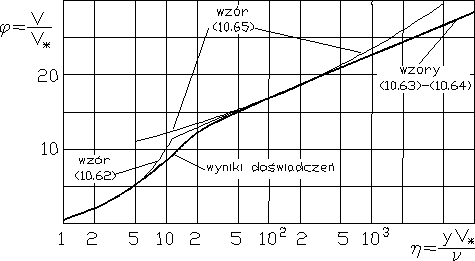
Rys. 10.4

Na rys. 10.4 zaznaczono też wykres funkcji potęgowej

(10.65)

przybliżającej funkcję (10.63) ÷ (10.64) - często bowiem w celu uproszczenia obliczeń rozkłady logarytmiczne są aproksymowane uniwersalnymi rozkładami potęgowymi, opisywanymi ogólnym wzorem

(10.66)

W warstwie przyściennej „zszytej” z podwarstwy laminarnej i z rdzenia turbulentnego o logarytmicznym rozkładzie prędkości, droga mieszania jest łamaną. W rzeczywistości droga mieszania zmienia się w sposób ciągły w poprzek warstwy. Stąd też w wielu obliczeniach droga mieszania aproksymowana jest wielomianem trzeciego stopnia postaci

gdzie
, podobnie jak κ , jest stałą empiryczną.

10.5. Przepływy turbulentne w przewodach

Przepływy turbulentne w przewodach o dowolnych przekrojach poprzecznych stanowią jeden z najstarszych działów mechaniki płynów i znajdują się w centrum zainteresowania praktyki inżynierskiej ze względu na swe zastosowania techniczne. Można je zaliczyć do grupy przepływów przyściennych ze względu na obecność powierzchni ograniczających, które wywierają dominujący wpływ na kształt prędkości średniej oraz na rozkłady wielkości charakteryzujących turbulencję przepływu. Ścisłe jednak podobieństwo między przepływem w swobodnej warstwie przyściennej, a przepływami w przewodach występuje tylko w bliskim sąsiedztwie ścianek. Poza tym obszarem oba rodzaje przepływów różnią się wzajemnie odrębnością warunków brzegowych, gdyż poza obszarem warstwy przyściennej przepływ wykazuje cechy przepływu potencjalnego (warstwa swobodna), a w przewodzie przepływ potencjalny praktycznie nie występuje (za wyjątkiem odcinka wstępnego - rys. 5.20), ponieważ w centralnej części przewodu zachodzi z reguły interakcja warstw przyściennych utworzonych na przeciwległych jego ściankach.

Ze względu na powszechność występowania, najczęściej rozważanym w literaturze przedmiotu jest przepływ przez przewody o przekrojach kołowych, w którym - podobnie jak w swobodnej warstwie przyściennej - można wyróżnić kilka stref:

- podwarstwę laminarną znajdującą się w bezpośrednim sąsiedztwie ścianki,

- strefę przejściową ujmowaną wraz z obszarem poprzednim wspólną nazwą warstwy lepkiej (0.3 ÷ 0.4 % średnicy kanału); jest to obszar, w którym lepkość mo-

lekularna odgrywa znaczącą rolę w wartości naprężeń stycznych i w którym odbywa się znaczna część zmian prędkości średniej i zmian wielkości charakteryzujących turbulencję przepływu,

- strefę w pełni rozwiniętego przepływu turbulentnego (jej górna granica jest określona współrzędną = 0.15 ÷ 0.20), tworzącą wraz z warstwą lepką obszar przyścienny przepływu w przewodzie; obowiązuje w niej logarytmiczne prawo rozkładu prędkości średniej (10.63),

- turbulentny rdzeń przepływu (80 ÷ 85 % średnicy przewodu), nie znajdujący się już pod bezpośrednim wpływem ścianek przewodu; jego znamiennymi cechami są: nieznaczna zmiana prędkości średniej oraz praktyczna stałość współczynnika lepkości turbulentnej w środkowym obszarze kanału.

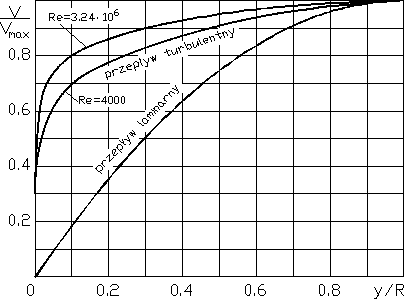
Rys. 10.5

Porównanie uśrednionych rozkładów prędkości
w rurze w przepływie laminarnym (przykład 8.3) i w przepływie turbulentnym (opartych na wynikach doświadczeń Nikuradsego) - przedstawia rys. 10.5. Z postaci tych rozkładów prędkości możemy łatwo wywnioskować, że składowa normalna gradientu prędkości na ściance jest w przypadku przepływu turbulentnego znacznie większa, niż w przypadku przepływu laminarnego - co oznacza, że

Zakładając, że wzór (10.63) stosuje się do przepływu przewodem osiowosymetrycznym, dla osi przewodu mamy

(10.67)

Ze związku między spadkiem ciśnienia
na odcinku przewodu na długości l, a naprężeniem stycznym na ściance

po zastąpieniu
zgodnie ze wzorem (5.22)

obliczamy

i następnie

(10.68)

Przepisując wzór (10.67) w postaci

i uwzględniając (10.68) otrzymamy wzór Prandtla-Karmana

(10.69)

gdzie stałe C i D zależą od doświadczalnie wyznaczonych parametrów κ i α oraz stosunku
szczególnym przypadkiem tego wzoru jest zależność (5.27).

Postępując w podobny sposób, przy wykorzystaniu funkcji (10.65), mamy

i następnie po podstawieniu związku (10.68) wyprowadzamy wzór Blasiusa (5.25).

Wpływ chropowatości na rozkład prędkości uśrednionej w przekroju poprzecznym rury jest przedstawiany za pomocą zmodyfikowanej funkcji (10.63)

(10.70)

gdzie k jest średnią wysokością występów chropowatości. Stąd po przyjęciu dalszych założeń co do postaci funkcji logarytmicznej, wynikają wzory (5.26), (5.28) oraz (5.29).

10.6. Op*r cia* poruszających się w cieczy lepkiej

Rozpatrując element
powierzchni ciała opływanego jednorodnym strumieniem cieczy lepkiej o prędkości
stwierdzamy, że działa na niego siła normalna - proporcjonalna do ciśnienia statycznego p oraz siła styczna - proporcjonalna do naprężenia stycznego
. Po obliczeniu wypadkowych tych sił działających na całą powierzchnię ciała i ich zrzutowaniu na kierunek prędkości
, otrzymamy opór całkowity X , który można traktować jako sumę oporu ciśnieniowego
oraz oporu tarcia

(10.71)

W cieczy doskonałej oba te składniki znikały, na mocy paradoksu d'Alemberta
i braku naprężeń stycznych. W cieczy lepkiej występuje natomiast zarówno opór ciśnieniowy, jak i opór tarcia, przy czym ich wielkość zależy od kształtu ciała, chropowatości jego powierzchni i zakresu liczb Reynoldsa.

W zakresie dużych liczb Reynoldsa, gdy przepływ w strumieniu jednorodnym w nieskończoności jest laminarny (ruch w atmosferze swobodnej), w czołowej części ciała o gładkich ściankach tworzy się laminarna warstwa przyścienna. Charakter przepływu w środkowej części tego ciała zależy więc zasadniczo od wzajemnego położenia punktu utraty stateczności warstwy laminarnej i punktu jej oderwania. Jeśli punkt oderwania warstwy przypada bliżej punktu spiętrzenia niż punkt utraty stateczności mówimy o przepływie podkrytycznym, gdy przypada dalej niż punkt utraty stateczności - o przepływie nadkrytycznym , wreszcie gdy oba te punkty pokrywają się - o przepływie krytycznym . Liczbę Reynoldsa odpowiadającą przepływowi krytycznemu nazywamy krytyczną liczbą Reynoldsa - jest ona oznaczana symbolem .

Rozkład ciśnienia na obwodzie walca w zakresie pod- i nadkrytycznym przedstawia rys. 10.6, na obwodzie kuli - rys. 10.7. Na podstawie tych rozkładów ciśnienia można łatwo wywnioskować, że w zakresie podkrytycznym, gdy warstwa laminarna odrywa się bez uprzedniego przekształcenia w warstwę turbulentną, opór obu ciał jest większy niż w zakresie nadkrytycznym. W zakresie nadkrytycznym warstwa turbulentna również ulega oderwaniu, jednak punkt jej oderwania jest zawsze przesunięty w kierunku przepływu, w porównaniu z punktem oderwania warstwy laminarnej - wskutek czego rozkład ciśnienia jest bardziej zbliżony do teoretycznego i w mniejszym stopniu jest zakłócona symetria opływu. Widać to wyraźnie na rysunkach przedstawiających: podkrytyczny (rys. 10.8) i nadkrytyczny (rys. 10.9) opływ kuli; w przypadku przepływu podkrytycznego występuje bowiem szeroki obszar zastoju, co wyjaśnia dużą asymetrię rozkładu ciśnienia.

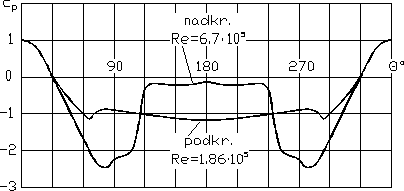
Rys. 10.6

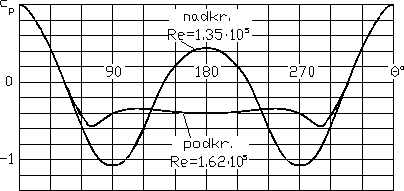
Rys. 10.7

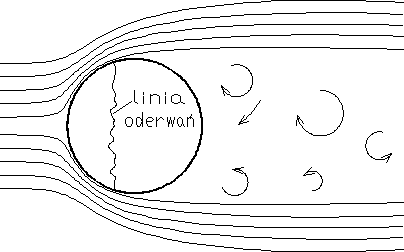
Rys. 10.8

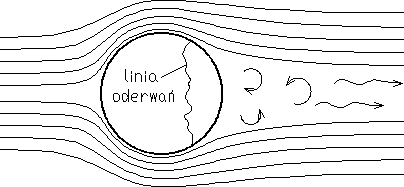
Rys. 10.9

Przedstawione wyniki zezwalają na sformułowanie ogólnych zasad zmniejszania oporu ciał dla przepływów przy dużych liczbach Reynoldsa. Podstawowym problemem jest zmniejszenie oporu ciśnieniowego, spowodowanego oderwaniem warstwy przyściennej i pojawieniem się obszaru zastoju. Toteż korzystne będą wszystkie czynniki zapobiegające oderwaniu warstwy lub też przesuwające punkt oderwania w kierunku krawędzi spływu. W zakresie podkrytycznym można to osiągnąć poprzez zwiększenie liczby Reynoldsa, zwiększenie chropowatości ścianek w przedniej części opływanych ciał i sturbulizowanie strumienia zewnętrznego - aby zapobiec oderwaniu laminarnej warstwy przyściennej. W zakresie nadkrytycznym siła oporu za-leży w sposób istotny od oporu tarcia, który może być znacznie zmniejszony w przypadku występowania możliwie długiej i statecznej laminarnej warstwy przyściennej - przykłady 9.4 i 10.3.

ĆWICZENIA

Przykład 10.1. Wyznaczyć przepływ w płaskiej strudze zatopionej (rys. 9.6) dla zadanego strumienia pędu P, przy założeniu symetrii ruchu.

Po pominięciu gradientu ciśnienia
i naprężenia laminarnego
pierwsze równanie układu (10.49) przyjmie postać

(10.72)

Całkowanie wzdłuż zmiennej grubości strugi, przy uwzględnieniu symetrii ruchu
oraz warunków znikania składowych prędkości:

i
na brzegach daje

lub w postaci równoważnej

gdyż Wynika stąd zależność analogiczna do zależności (9.67)

Dla zamknięcia układu równań skorzystamy z modelu Boussinesqa. Zgodnie ze wzorem (10.35) mamy

(10.73)

Uwzględniliśmy tu, że lepkość turbulentna
jest funkcją x, natomiast w przekroju poprzecznym strugi (x = const) jest ona stała. Takie założenie jest słuszne wszędzie za wyjątkiem sąsiedztwa brzegów , gdzie występuje przepływ naprzemienny, tzn. przepływ na przemian laminarny i turbulentny.

Równanie (10.72) zapisujemy z uwzględnieniem wzoru (10.73)

i następnie wyrażamy składowe prędkości i przez uśrednioną funkcję prądu

Otrzymujemy równanie

które po wprowadzeniu zmiennej niezależnej

jest identyczne z równaniem dla strugi laminarnej dla ν = 1 (przykł. 9.1)

Należy jeszcze określić postać nieznanej funkcji Dla *
otrzymujemy

gdzie C jest stałą wyznaczaną eksperymentalnie.

Przykład 10.2. Wyznaczyć płaski przepływ turbulentny, stacjonarny względem wielkości uśrednionych, w pasie nieograniczonym, zawartym między dwiema ścianami równoległymi (rys. 8.8).

W pełnym układzie równań (10.31), odniesionych do płaskiego, stacjonarnego ruchu uśrednionego cieczy lepkiej:

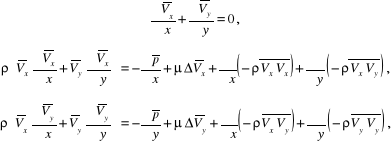
dokonujemy następujących uproszczeń:

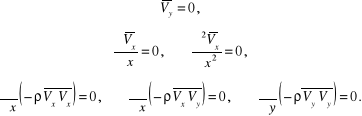
Cały układ równań redukuje się więc do równania

gdzie C jest stałą.

Zakładając, że wszędzie w rozpatrywanym przepływie naprężenie laminarne jest pomijalnie małe w porównaniu z naprężeniem turbulentnym - na mocy (10.52) ma-my

Po jednokrotnym scałkowaniu powyższego wzoru i przyjęciu l zgodnie z (10.42) dostajemy

Ze względu na symetrię ruchu uśrednionego musi być (rys. 8.8)

skąd wynika

Niech na ściance naprężenie przybiera szczególną wartość

wobec czego

Otrzymane równanie daje się scałkować jednokrotnie, po czym po uwzględnieniu dodatkowego warunku dotyczącego gradientu prędkości na ściance

uzyskujemy

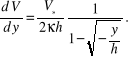
Po kolejnym scałkowaniu i wyznaczeniu stałej całkowania z warunku

wzór na rozkład prędkości przybiera ostatecznie następującą postać

,

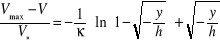
w której zgodnie z wynikami doświadczeń należy przyjąć κ = 0.3 ÷ 0.4.

Przykład 10.3. Wyznaczyć turbulentną warstwę przyścienną na gładkiej płytce przy wykorzystaniu wzoru całkowego Karmana (9.43).

Zakładamy, że turbulentna warstwa przyścienna rozpoczyna się już na krawędzi natarcia płytki: i opieramy się na rozkładzie uniwersalnym (10.65)

Na granicy warstwy przyściennej mamy:

toteż wzór na rozkład prędkości przybiera ostatecznie postać

Postępując dalej tak samo jak w przykładzie 9.4, kolejno obliczamy:

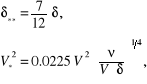
i wyznaczamy grubość warstwy przyściennej z równania różniczkowego

w postaci następującej funkcji

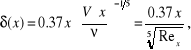
(10.74)

gdzie

Zatem grubość turbulentnej warstwy przyściennej * rośnie szybciej ze zmianą współrzędnej x, niż grubość warstwy laminarnej * i również większy jest opór tarcia obu stron płytki, przypadający na jej długość l

(10.75)

Powtarzając obliczenia turbulentnej warstwy przyściennej na płytce w opisany sposób, ale biorąc jako podstawę uniwersalny rozkład logarytmiczny (10.63) z parametrami (10.64), zamiast rozkładu potęgowego otrzymujemy nieco inną formułę wyrażającą opór tarcia

, (10.76)

która przy dużych () lepiej zgadza się z doświadczeniem, niż wzór poprzedni (rys. 10.4).

Przykład 10.4. Samolot leci z prędkością w powietrzu, którego współczynnik lepkości kinematycznej
Korzystając ze wzorów dla płyt płaskich, obliczyć współczynnik oporu tarcia oraz grubość warstwy przyściennej na krawędzi spływu płata o cięciwie l = 2.40 m.

Dla samolotu lecącego z prędkością

liczba Reynoldsa wynosi

, wobec tego warstwa przyścienna jest burzliwa.

Do obliczenia współczynnika oporu tarcia wykorzystujemy zależność (10.76)

a grubość warstwy przyściennej na krawędzi spływu wyznaczamy ze wzoru (10.74)

Przykład 10.5. Obliczyć opór tarcia gładkiej płyty o cięciwie l = 1 m i rozpiętości L = 4 m, ustawionej równolegle do kierunku przepływającej wody o gęstości oraz współczynniku lepkości kinematycznej w temperaturze
Zadanie rozwiązać, przyjmując prędkość wody równą:

a)

b)

a. Dla liczby Reynoldsa

mniejszej od współczynnik oporu obliczamy ze wzoru (10.75)

Siła oporu tarcia jest równa

(10.77)

gdzie

zatem

b. Dla prędkości
liczba Reynoldsa

jest większa od do wyznaczenia współczynnika oporu wykorzystujemy więc wzór (10.75)

i następnie po podstawieniu do (10.77) mamy

Przykład 10.6. Nafta o kinematycznym współczynniku lepkości oraz gęstości (przy T = 283 K) opływa gładką nieruchomą płytę, wstawioną równolegle do kierunku przepływu. Prędkość cieczy w obszarze niezakłóconym Obliczyć wartość oraz stosunek naprężeń stycznych w punktach oddalonych od krawędzi natarcia płyty o i

Odległość od krawędzi natarcia punktu, w którym warstwa przyścienna laminarna przechodzi w turbulentną wynika ze wzoru

.

Ponieważ dla płyt płaskich
zatem

.

Wynika stąd, że w odległości
od krawędzi natarcia warstwa przyścienna jest laminarna, natomiast w punkcie oddalonym o
burzliwa.

W odległości
= 0.4 m od krawędzi natarcia liczba Reynoldsa wynosi

a naprężenie styczne na powierzchni płyty przy laminarnej warstwie przyściennej, będące wynikiem rozwiązania równania (9.35), jest równe

W odległości
= 1.2 m od krawędzi natarcia

stąd

Stosunek naprężeń stycznych

310

---