w której współczynnik przepuszczalności
zależy wyłącznie od fizycznych własności ośrodka.

Zastępując iloraz prędkością filtracji V, na podstawie wzoru (11.22) możemy zapisać prawo Darcy'ego w postaci

(11.25)

w której został wprowadzony znak minus, uwzględniający przeciwny zwrot prędkości do zwrotu osi z - i następnie, po przejściu do granicy, w postaci różniczkowej:

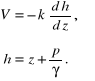
(11.26)

Uogólniając ten wzór, w przestrzennym układzie współrzędnych prostokątnych możemy napisać

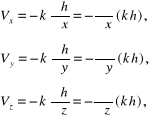
(11.27)

skąd wynika, że składowe prędkości filtracji można wyrazić za pomocą pochodnych cząstkowych funkcji
zwanej potencja*em pr*dkości filtracji :

Na mocy równania ciągłości zagadnienie wyznaczania ruchu wód swobodnych w jednorodnym ośrodku porowatym (gruncie) sprowadza się więc do rozwiązania równania Laplace'a

(11.28)

z warunkami brzegowymi zależnymi od tego, czy powierzchnie ograniczające są przepuszczalne, nieprzepuszczalne, czy też są powierzchniami swobodnymi.

Na podstawie doświadczeń ustalono, że ruch cieczy w ośrodku porowatym podlega liniowemu prawu Darcy'ego w zakresie małych liczb Reynoldsa

(11.29)

gdzie d jest średnicą ziaren ośrodka porowatego.

ĆWICZENIA

Przykład 11.1. Dla obliczenia współczynnika oporu samochodu wyścigowego o długości l = 5 m i rozwijającego prędkość V = 220 
wykonano model w skali 1:10 i zbadano w tunelu wodnym. Z jaką prędkością musi przepływać woda w tunelu, aby zachowane było pełne podobieństwo dynamiczne przepływu? Temperatura wody t = 20°C.

W temperaturze t = 20°C lepkości kinematyczne powietrza i wody są równe: , = 0.01; z równości liczb Reynoldsa

mamy

.

Przykład 11.2. Z jaką prędkością musi poruszać się model statku, aby zachowane było podobieństwo dynamiczne:

a) przy uwzględnieniu sił lepkości,

b) przy uwzględnieniu sił ciężkości.

Model jest wykonany w skali 1:10. Statek porusza się z prędkością = 36

a) z równości liczb Reynoldsa znajdujemy

skąd obliczamy

b) z równości liczb Froude'a

mamy

Przykład 11.3. Posługując się metodą analizy wymiarowej wyprowadzić zależność strat liniowych ciśnienia
od średnicy przewodu d, jego długości l, własności fizycznych cieczy: gęstości ρ i współczynnika lepkości dynamicznej μ, średniej prędkości przepływu w poprzecznym przekroju przewodu V oraz średniej chropowatości k.

Poszukiwaną zależność zapiszemy w postaci

(11.30)

W zależności (11.30) mamy wielkości, których wymiary zawierają jednostki podstawowe: L , M , T.

Zgodnie z twierdzeniem π (11.18) równanie (11.30) można przedstawić za pomocą wzoru zawierającego bezwymiarowych parametrów

(11.31)

W celu wyznaczenia parametrów
obieramy trzy wielkości podstawowe, np.:
które zawierają wszystkie jednostki podstawowe i są od siebie wymiarowo niezależne

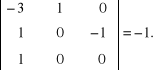
Tworzymy cztery iloczyny bezwymiarowe:

Z porównania wykładników potęg przy jednostkach podstawowych wynikają na-stępujące układy równań:

a) obliczanie parametru π:

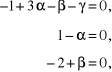
b) obliczanie parametru

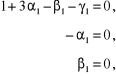
c) obliczanie parametru

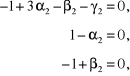
d) obliczanie parametru

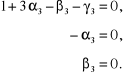
Po rozwiązaniu tych układów równań otrzymujemy:

a)

b)

c)

d)

i następnie bezwymiarowe parametry podobieństwa:

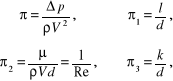
które podstawiamy do równania (11.31) uzyskując związek

Ze związku tego, przy założeniu
, wynika znany wzór Darcy'ego-Weisbacha (5.22).

Przykład 11.4. Stosując analizę wymiarową wyprowadzić ogólne równanie na ciśnienie, wywierane na ciało przez ciecz.

Ogólny wzór na ciśnienie można wyrazić następująco

(11.32)

gdzie l jest wymiarem charakterystycznym ciała poruszającego się z prędkością w cieczy o gęstości ρ i lepkości μ, przy czym przyspieszenie grawitacyjne wynosi g, a napięcie powierzchniowe cieczy σ.

Wybieramy bazę składającą się z wielkości: ρ , V, L :

i sprawdzamy ich liniową niezależność

Zgodnie z twierdzeniem Buckinghama liczba bezwymiarowych iloczynów wyniesie: q = 4. Tworzymy więc kombinacje ciśnienia p z wielkościami fizycznymi

i następnie równanie (11.32) zapisujemy w postaci

Po wyrażeniu wielkości fizycznych p, μ , g i σ w układzie M L T :

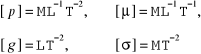
i wyznaczeniu wykładników potęgowych z odpowiednich układów równań (11.20) otrzymujemy następujące parametry podobieństwa:

− bezwymiarowe ciśnienie,

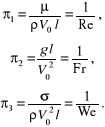
Przykładowo wykładniki potęgowe określające parametr podobieństwa π tworzą układ równań:

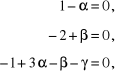
którego rozwiązaniem są wartości wykładników:

Dodatkowo otrzymaliśmy informację o strukturze wzoru wyrażającego ciśnienie: jest to iloczyn
i bezwymiarowej funkcji π, jako współczynnika

Przykład 11.5. Anemometr czaszowy (rys. 11.21), wstawiony w strumień przepływającego powietrza, obraca się ze stałą prędkością kątową ω. Pomijając opory tarcia oraz zakładając, że współczynnik siły nośnej dla czasz ustawionych wzdłuż kierunku przepływu jest równy zeru, wyznaczyć prędkość powietrza. Przyjąć promień wirnika równy R oraz współczynniki dla czaszy wklęsłej i kulistej równe: = = 1.33, = 0.34.

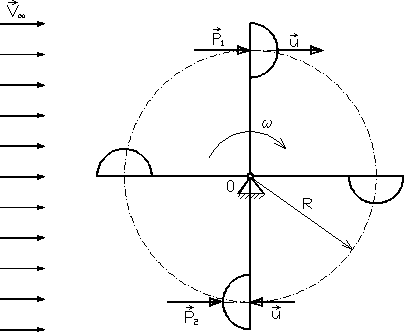
Rys. 11.21

Prędkość kątowa wirnika ω = const, zatem suma momentów pochodząca od sił aerodynamicznych względem osi O wirnika jest równa zeru, czyli

(11.33)

Poszczególne siły wynoszą:

, (11.34)

. (11.35)

Podstawiając zależności (11.34) i (11.35) do równania (11.33) i uwzględniając przy tym, że

otrzymujemy

stąd

.

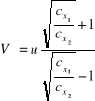
Prędkość unoszenia jest równa

przeto prędkość powietrza wynosi

Przykład 11.6. Dana jest prostokątna komora filtracyjna o wymiarach i wypełniona trzema jednakowej grubości warstwami filtracyjnymi o współczynnikach filtracji równych:

Obliczyć przepływ wody przez komorę, jeżeli różnica poziomów wody w komorze filtracyjnej i w komorze czerpnej przy ustalonym przepływie wynosi
pomijając straty na poziomym przepływie wody.

Wyrazimy różnicę poziomów wody w komorze filtracyjnej i komorze czerpnej za pomocą strat ciśnienia na poszczególnych warstwach filtracyjnych

które obliczamy z prawa Darcy'ego (11.26):

Uwzględniając ciągłość ruchu cieczy

oraz jednakową wysokość warstw filtracyjnych

mamy

a stąd

.

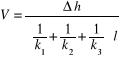
i następnie

.

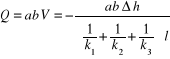
Po podstawieniu wartości liczbowych otrzymamy

330

---