7. Jednowymiarowe przepŁywy gazu

7.1. Zależności podstawowe

Przedmiotem niniejszego rozdziału jest badanie zagadnień jednowymiarowego ruchu gazu nielepkiego i nie przewodzącego ciepła, a doskonałego w sensie termodynamicznym, tzn. spełniającego równanie Clapeyrona (1.13).

Zmianę stanu gazu mogą spowodować procesy natury mechanicznej i procesy natury cieplnej. Do pierwszych zaliczamy pracę wykonaną podczas sprężania lub rozprężania gazu. Do drugich należy wymiana ciepła między gazem a otoczeniem, albo między elementami gazu.

Z pierwszej zasady termodynamiki zastosowanej do jednostki masy gazu układu zamkniętego wynika, że jeśli energia kinetyczna oraz energia potencjalna nie ulegają zmianie, to ciepło d q dostarczone do układu oraz wykonana nad nim praca zewnętrzna d l (dodatnia - wykonana przez układ) powodują przyrost jego energii wewnętrznej

(7.1)

gdzie

(7.2)

Jest przy tym istotne, że dla dowolnych przemian przyrosty
i
nie są różniczkami zupełnymi, gdyż zależą również od sposobu, w jaki przemiana zachodzi, a nie tylko od stanu początkowego i stanu końcowego gazu.

Zmiana energii wewnętrznej jest proporcjonalna do zmiany temperatury

(7.3)

gdzie
jest ciepłem właściwym przy stałej objętości. Jeśli wymiana ciepła odbywa się przy stałym ciśnieniu, to

(7.4)

gdzie jest ciepłem właściwym przy stałym ciśnieniu.

Z równania Clapeyrona (1.13) obliczamy

(7.5)

i następnie, na mocy (7.1) i (7.2), przy const, otrzymujemy równanie Meyera (1.15). Z tego równania i definicji wykładnika adiabaty (1.14) mamy:

(7.6)

Za pomocą parametrów u, p i ρ definiuje się nowy parametr stanu zwany entalpią

(7.7)

Po jego zróżniczkowaniu i podstawieniu zależności (7.1) ÷ (7.2) uzyskujemy

(7.8)

zatem przy const na mocy (7.4) jest

(7.9)

Następnie, biorąc pod uwagę związki (7.6) oraz równanie Clapeyrona (1.13), entalpię można zapisać również następująco:

(7.10)

Zmiana entropii gazu w przemianie elementarnej jest definiowana jako ilość wymienionego ciepła odniesiona do temperatury

(7.11)

Związek ten przekształcamy przy wykorzystaniu zależności (7.1) i równania stanu (1.13)

(7.12)

oraz całkujemy wyznaczając stałą całkowania z warunków początkowych:

(7.13)

Wyrażając stosunek temperatur przez stosunek ciśnień i gęstości mamy

(7.14)

lub też

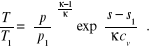
(7.15)

Dla przepływów izentropowych (const) z równań (7.13) ÷ (7.15) wynikają związki opisywane równaniem izentropy (1.14):

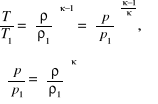
(7.16)

*

W celu wyznaczenia prędkości ruchu fali dźwiękowej oraz prędkości rozchodzenia się nieskończenie słabych zaburzeń rozważymy płaską falę dźwiękową poruszającą się w określonym kierunku; mogą to być np. kolejne zgęszczenia i rozrzedzenia wywołane nagłym ruchem tłoka w cylindrze.

Zmiany pędu warstwy gazu

możemy zapisać w postaci

(7.17)

w której a jest prędkością dźwięku, σ - polem przekroju cylindra,
- natężeniem przepływu (3.22), spowodowanym zmianą ciśnienia
Konsekwencją zmiany ciś-nienia jest zmiana gęstości, stąd jest

i następnie

(7.18)

Fala dźwiękowa porusza się szybko - można więc przyjąć, że lokalne sprężenie ma charakter izentropowy i wykorzystać wzór (1.14), z którego wyznaczamy

(7.19)

i ostatecznie, biorąc dodatkowo pod uwagę równanie stanu (1.13) i zależności (7.10), mamy

(7.20)

Można teraz obliczyć stosunek lokalnej prędkości przepływu do lokalnej prędkości dźwięku, nazywany liczbą Macha

(7.21)

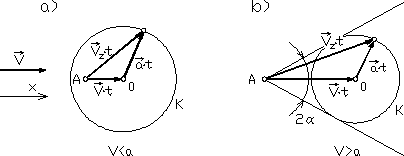
Rys. 7.1

Łatwo można stwierdzić, że rozprzestrzenianie się słabych zaburzeń ma zupełnie inny charakter w zależności od tego czy przepływy są poddźwiękowe, czy też naddźwiękowe. Rozważmy w tym celu opływ pewnego nieruchomego punktu A strumieniem gazu, poruszającym się ze stałą prędkością
wzdłuż osi x (rys. 7.1).

Opływ punktu A powoduje zaburzenia, które są unoszone strumieniem gazu i które rozprzestrzeniają się jednocześnie we wszystkich kierunkach z prędkością dźwięku a. Ich prędkość względem układu nieruchomego wynosi zatem

Jeśli zaburzenia powstały w chwili po pewnym czasie t znajdą się one na powierzchni kuli K o promieniu a t i środku O, odległym od punktu A o drogę V t. Widzimy, że w przepływie poddźwiękowym zaburzenia rozprzestrzeniają się w całej objętości (rys. 7.1a) i dotrą po pewnym czasie do każdego punktu przestrzeni; natomiast w przepływie naddźwiękowym obszar rozchodzenia się zaburzeń mieści się w stożku o kącie wierzchołkowym 2 α (rys. 7.1b), określonym zależnością

(7.22)

Oznacza to, że zaburzenia akustyczne w przepływie poddźwiękowym są słyszalne wszędzie, natomiast w przepływie naddźwiękowym są słyszalne jedynie w stożku nazywanym stożkiem Macha .

7.2. R*wnanie Bernoulliego

Rozważając przepływy gazów można zaniedbać siły masowe, gdyż są one pomijalnie małe.

Przyjmując związek między ciśnieniem i gęstością dla przemiany adiabatycznej (1.14) obliczamy funkcję ciśnienia (2.11)

(7.23)

Po podstawieniu do wzoru (4.10), równanie Bernoulliego dla gazów przybiera następującą formę

(7.24)

gdzie symbol jest stałą Bernoulliego, która oznacza energię całkowitą, odniesioną do jednostki masy (5.3).

Biorąc pod uwagę zależności (7.20) oraz całkując związek (7.9)

(7.25)

możemy przedstawić równanie Bernoulliego (7.24) również w czterech następujących postaciach:

(7.26)

(7.27)

(7.28)

(7.29)

Temperatura gazu nie może spaść poniżej zera absolutnego; z równania (7.29) wynika więc wniosek o istnieniu prędkości maksymalnej

(7.30)

Prędkość gazu nie może zatem wzrastać nieograniczenie - przeciwnie niż w przypadku cieczy doskonałej.

Przy wyznaczaniu ruchu gazu często wygodnie jest odnosić jego parametry lokalne do parametrów gazu w punkcie spiętrzenia, które nazywane są parametrami spiętrzenia (oznaczamy je indeksem dolnym ₀). Podstawiając w równaniach (7.24), (7.26) ÷ (7.29) otrzymujemy

(7.31)

Lokalne parametry gazu odnosi się również często w dynamice gazów do parametrów krytycznych gazu, które wywodzą się z pojęcia prędkości krytycznej (oznaczamy je indeksem dolnym ).

Prędkość gazu nazywa się krytyczną, jeśli w pewnym punkcie pola prędkość gazu jest równa jego lokalnej prędkości dźwięku

(7.32)

w innych punktach pola prędkości mogą być więc podkrytyczne , gdy

(7.33)

lub też nadkrytyczne , gdy

. (7.34)

Wynika stąd możliwość przyjęcia prędkości krytycznej jako prędkości odniesienia, zamiast lokalnej prędkości dźwięku (7.21); otrzymany stosunek nazywa się prędkością bezwymiarową

(7.35)

Wykorzystując wzór (7.32) z równania (7.26) wyznaczamy

(7.36)

i następne zależności z równań (7.24) oraz (7.27) ÷ (7.29)

(7.37)

Reasumując stwierdzamy, że stałą Bernoulliego możemy wyrazić w trojaki sposób:

- poprzez prędkość maksymalną gazu (7.30),

- poprzez parametry gazu w punkcie spiętrzenia (7.31),

- poprzez parametry krytyczne (7.36) ÷ (7.37).

*

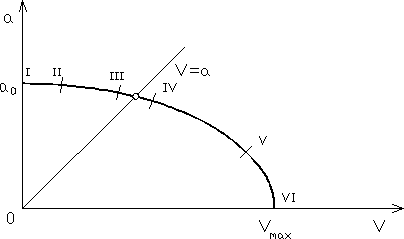
Rys. 7.2

Ze względu na jakościowo odmienny ruch gazu w różnych zakresach liczby Macha i możliwość stosowania różnych uproszczeń natury matematycznej stosowany jest podział przepływów gazu. Może on być dokonany w oparciu o tzw. elipsę pr*dkości przedstawioną na rys. 7.2, której równanie

(7.38)

wynika ze wzorów (7.26), (7.30) i (7.31)

.

Na rys. 7.2 zaznaczono pięć umownych zakresów przepływu określonych zależnością pomiędzy modułem prędkości przepływu i modułem prędkości dźwięku:

I-II. Przepływ nieściśliwy. Zmiany prędkości powodują nieznaczne zmiany prędkości dźwięku (Ma < 0.3).

II-III. Przepływ poddźwiękowy. Zmiany prędkości powodują wyraźne zmiany prędkości dźwięku (Ma = 0.3 ÷ 0.8).

III-IV. Przepływ okołodźwiękowy (transoniczny). Prędkość przepływu jest równa lub bliska prędkości dźwięku (Ma = 0.8 ÷ 1.5).

IV-V. Przepływ naddźwiękowy. Zmiany prędkości dźwięku są rzędu zmian prędkości przepływu (Ma = 1.5 ÷ 5.0).

V-VI. Przepływ hiperdźwiękowy. Niewielkim zmianom prędkości towarzyszą duże zmiany prędkości dźwięku (Ma > 5.0).

Pomiędzy parametrami lokalnymi gazu, parametrami spiętrzenia i parametrami krytycznymi można uzyskać wiele związków, pomocnych w różnych zastosowaniach. Z równania Bernoulliego zapisanego w postaci

wyprowadzamy związek między liczbą Macha M oraz prędkością bezwymiarową λ

(7.39)

W podobny sposób, przy wykorzystaniu wcześniej wyznaczonych zależności stwierdzamy, że

(7.40)

i następnie na mocy (1.14) mamy

174

---