4. Podstawowe rÓwnania
dynamiki pŁynÓw nielepkich

4.1. R*żniczkowe r*wnania ruchu Eulera

Płyn nielepki jest uproszczonym modelem płynu rzeczywistego, w którym zakładamy występowanie wyłącznie naprężeń normalnych (pochodzących od ciśnienia) i pomijamy wpływ sił pochodzących od naprężeń stycznych. Założenie to jest wprowadzane głównie ze względu na wielkie trudności matematyczne związane z rozwiązywaniem układu równań różniczkowych opisujących ruch płynu lepkiego. Jest ono jednak uzasadnione, gdyż najczęściej występujące w przyrodzie płyny: powietrze i woda, odznaczają się małą lepkością, a wyniki teoretyczne przy założeniu braku naprężeń stycznych są w wielu przypadkach zadziwiająco zgodne z wynikami doświadczeń. Zawsze jednak w konkretnych zastosowaniach należy brać pod uwagę ograniczoność teorii płynów nielepkich.

Zakładając, że ruch płynu został określony za pomocą pola prędkości

pola gęstości oraz pola ciśnienia rozpatrzymy równowagę elementu płynu przedstawionego na rysunku 2.2; masa płynu o gęstości ρ zawartego w elementarnym prostopadłościanie wynosi

Na rozważany element płynu działają trzy rodzaje sił, których rzuty na kierunki
są następujące:

a) siły masowe:

określone przez pole jednostkowych sił masowych
,

b) siły powierzchniowe spowodowane działaniem ciśnienia statycznego (2.1), działające normalnie na ścianki elementarnego prostopadłościanu

c) siły bezwładności, jako przeciwne do składowych przyspieszenia (3.9) elementu płynu:

Zgodnie z zasadą d'Alemberta suma wszystkich sił rzeczywistych i sił bezwładności na dowolny kierunek jest równa zeru. Pisząc więc warunki równowagi dla osi otrzymamy układ równań różniczkowych opisujących ruch płynu nielepkiego:

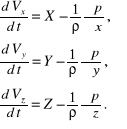
(4.1)

Równania te są równoważne jednemu równaniu wektorowemu

(4.2)

które po wykorzystaniu zależności (3.11) można przepisać również w postaci

(4.3)

Otrzymane równanie Eulera, w połączeniu z równaniem ciągłości (3.18) i równaniem stanu (1.13) dla gazu doskonałego, opisują ruch płynów nielepkich w najogólniejszej postaci.

W niektórych zastosowaniach przydatna bywa taka postać równania Eulera, w której wyraźnie występuje rotacja prędkości. Postać ta nosi nazwę równania Eulera w formie Lamba i Gromeki , a jej wyprowadzenie opiera się na zależności (przykład 4.1)

(4.4)

między pochodną substancjalną prędkości a rotacją prędkości; ma ona zatem następującą postać

(4.5)

4.2. Ca*ki r*wnania Eulera

Istnieją dwie całki równania Eulera o charakterze ogólnym. Dają one bezpośredni związek między prędkością, ciśnieniem i gęstością płynu, a więc parametrami najbardziej istotnymi z technicznego punktu widzenia.

Przy obliczaniu obu całek przyjmuje się dwa wspólne założenia upraszczające:

a) potencjalność pola jednostkowych sił masowych (2.14),

b) barotropowość płynu (2.10).

Całkę, zwaną całką Cauchy'ego i Lagrange'a otrzymujemy z rów-nania Eulera w formie Lamba i Gromeki (4.5) przy dodatkowym założeniu, że ruch jest bezwirowy. Oznacza to potencjalność pola prędkości

(4.6)

wobec czego

Przy powyższych założeniach równanie (4.5) można przepisać w postaci

lub też w postaci równoważnej

Gradient oznacza różniczkowanie względem współrzędnych przestrzennych, zatem funkcja, na którą działa w powyższym wzorze, może zależeć tylko od czasu

(4.7)

Dowolna funkcja występująca w całce Cauchy'ego i Lagrange'a (4.7) jest określana na podstawie warunków początkowych zagadnienia; dla przepływu ustalonego ma ona jednakową wartość w całym obszarze ruchu płynu

(4.8)

Przyjmując stacjonarność ruchu jako trzecie założenie upraszczające otrzymuje się drugą całkę równania Eulera, zwaną całką Bernoulliego.

Przy tych założeniach równanie Lamba-Gromeki jest następujące

Mnożąc je następnie skalarnie przez wektor prędkości
otrzymujemy

(4.9)

ponieważ

Z analizy zależności (4.9) wynikają następujące wnioski:

a) grad
jest więc również ortogonalny do linii, do których styczne są wektory prędkości - własność tę mają linie prądu,

b) gradient jest ortogonalny do powierzchni stałego skalara, na który działa; zatem wzdłuż linii prądu otrzymamy związek

(4.10)

Równanie (4.10) nazywamy równaniem Bernoulliego, a wartość stałej występującej w tym równaniu zależy tylko od rotacji pola prędkości; w polu bezwirowym jest jednakowa na wszystkich liniach prądu.

4.3. Ruch wirowy

Zbadamy zmiany, jakich doznaje cyrkulacja prędkości

(4.11)

wzdłuż poruszającej się linii płynnej l.

W tym celu obliczymy pochodną substancjalną cyrkulacji (4.11)

Różniczkowanie jest złożone, albowiem rozważana linia jest zmienna w czasie. W celu obejścia tych trudności wprowadzimy zmienne Lagrange'a. Niech σ będzie zmienną określającą położenie elementu płynu na linii płynnej w pewnej ustalonej chwili; nie zależy ona od czasu. Położenie elementu płynu należącego do linii płynnej AB względem układu O x y z opisuje promień wodzący tego elementu (rys. 4.1)

;

prędkość elementu jest jego pochodną

a różniczka łuku
jest identyczna z przesunięciem końca promienia wodzącego wzdłuż tej linii przy ustalonym czasie i wynosi

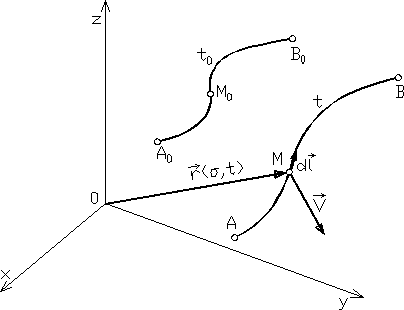
Rys. 4.1

Dokonując zamiany zmiennych w całce obliczamy

Funkcja podcałkowa w drugiej całce może być zapisana w postaci

i ostatecznie otrzymamy wzór

(4.12)

wyrażający tzw. twierdzenie Kelvina o pochodnej cyrkulacji.

Jeśli linia płynna jest zamknięta, pochodna cyrkulacji zależy wyłącznie od cyrkulacji przyspieszenia

(4.13)

Zgodnie z równaniem Eulera (4.2) przyspieszenie jest wyrażone sumą

Zakładając barotropowość płynu i potencjalność pola sił masowych jednostkowych, dla dowolnej linii płynnej zamkniętej obliczamy

(4.14)

W ten sposób udowodniliśmy tzw. twierdzenie Lagrange'a odnoszące się do trwałości ruchu wirowego: jeżeli w pewnym obszarze płynnym nie ma wirowości w określonej chwili, to nie było jej nigdy w tym obszarze, ani też nigdy nie może się ona w nim pojawić (przy powyższych założeniach).

W oparciu o wzór (4.14) można również uzasadnić twierdzenie Helmholtza o trwałości powierzchni i linii wirowych oraz o trwałości natężenia wirowości w rur-ce wirowej.

Weźmy pod uwagę zbiór elementów płynu tworzących w pewnej chwili powierzchnię wirową σ. Na powierzchni tej, zgodnie z jej definicją, jest

76

---