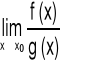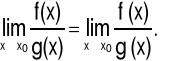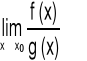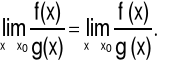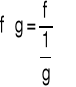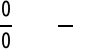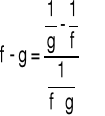V. twierdzenia o funkcjach z pochodnymi

5.3 Twierdzenia o granicach nieoznaczonych

Twierdzenie (Reguła de L'Hôspitala dla symbolu
)

Jeżeli funkcje f oraz g spełniają warunki:

	(5.3.1)
istnieje granica właściwa (niewłaściwa),to	(5.3.2)
	(5.3.3)

Twierdzenie (Reguła de L'Hôspitala dla symbolu
)

Jeżeli funkcje f oraz g spełniają warunki:

	(5.3.4)
istnieje granica właściwa (niewłaściwa),to	(5.3.5)
	(5.3.6)

Uwaga:

Reguła de L'Hôspitala jest prawdziwa także dla granic jednostronnych oraz dla granic przy x→-∞ lub x→+∞.

V. twierdzenia o funkcjach z pochodnymi

5.4 Tożsamości zmieniające rodzaje nieoznaczoności

Tabela

Nieoznaczoność	Stosowana tożsamość	Otrzymana nieoznaczoność

Uwaga:

Tożsamość podana dla symbolu ∞-∞ stosujemy dopiero wtedy, gdy zawiodą inne sposoby jej usuwania.

5.3 Twierdzenia o granicach nieoznaczonych

Reguła de L'Hôspitala dla symbolu

Przykład 1 Obliczyć granicę funkcji:

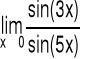
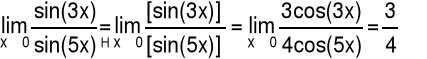
Przykład 2 Obliczyć granicę funkcji:

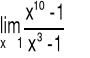
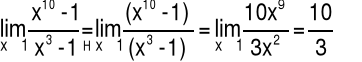
Przykład 3 Obliczyć granicę funkcji:

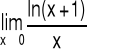
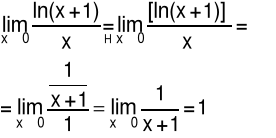
5.3 Twierdzenia o granicach nieoznaczonych

Reguła de L'Hôspitala dla symbolu

Przykład 4 Obliczyć granicę funkcji:

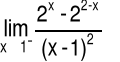
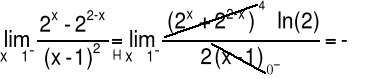
Przykład 5 Obliczyć granicę funkcji:

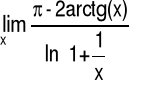
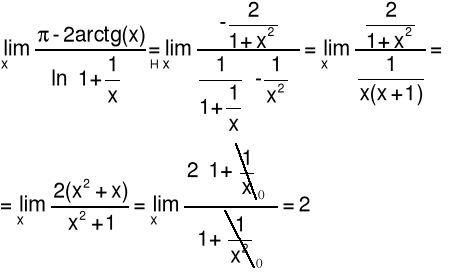
5.3 Twierdzenia o granicach nieoznaczonych

Reguła de L'Hôspitala dla symbolu

Przykład 1 Obliczyć granicę funkcji:

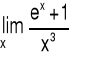
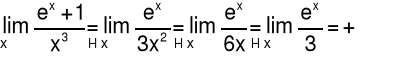
Przykład 2 Obliczyć granicę funkcji:

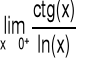
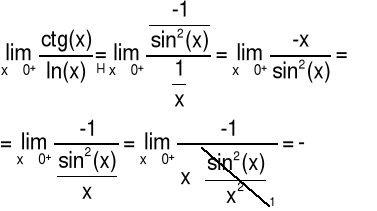
Przykład 3 Obliczyć granicę funkcji:

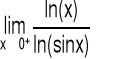
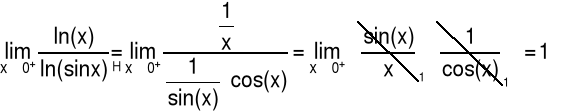
5.3 Twierdzenia o granicach nieoznaczonych

Obliczanie granic dla symbolu ∞-∞

Przykład 1 Obliczyć granicę funkcji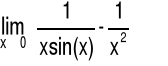

Sposób 1

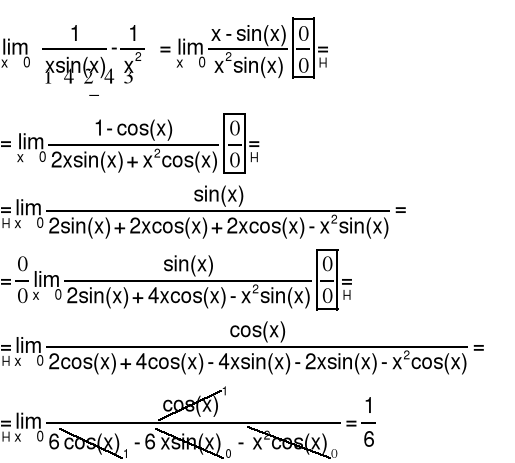
Sposób 2

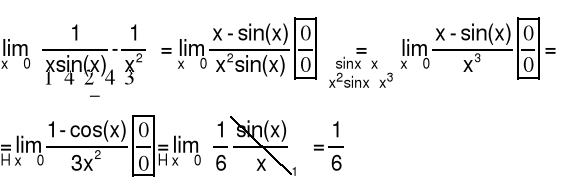
5.3 Twierdzenia o granicach nieoznaczonych

Obliczanie granic dla symbolu ∞-∞

Przykład 2 Obliczyć granicę funkcji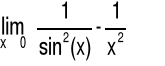

Sposób 1

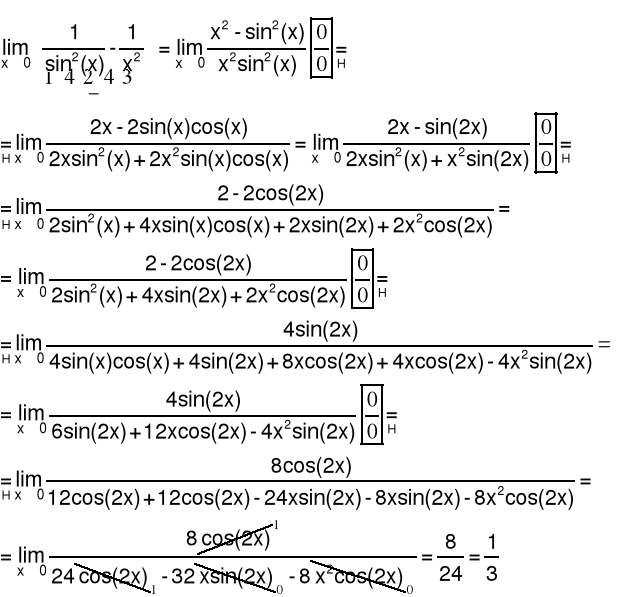
Sposób 2

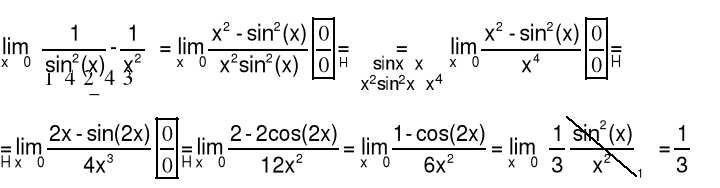
5.3 Twierdzenia o granicach nieoznaczonych

Obliczanie granic dla symbolu 0⁰

Przykład 1 Obliczyć granicę funkcji

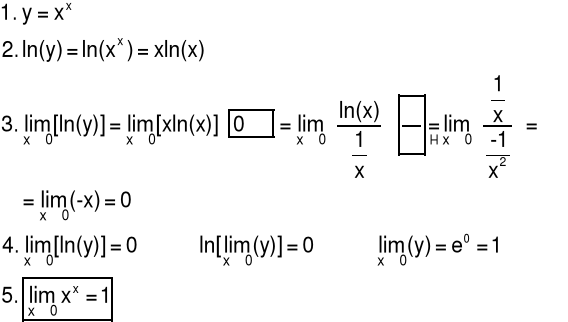
Przykład 2 Obliczyć granicę funkcji

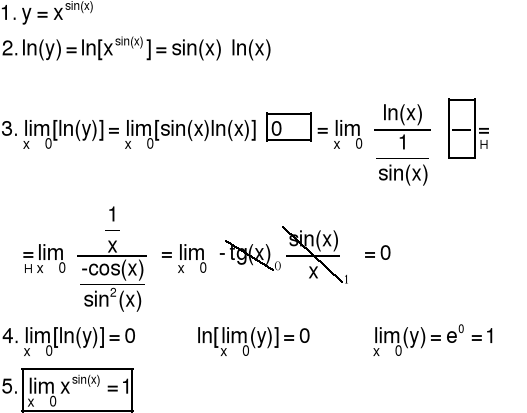
5.3 Twierdzenia o granicach nieoznaczonych

Obliczanie granic dla symbolu 1^∞

Przykład 1 Obliczyć granicę funkcji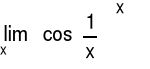

Przykład 2 Obliczyć granicę funkcji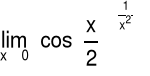

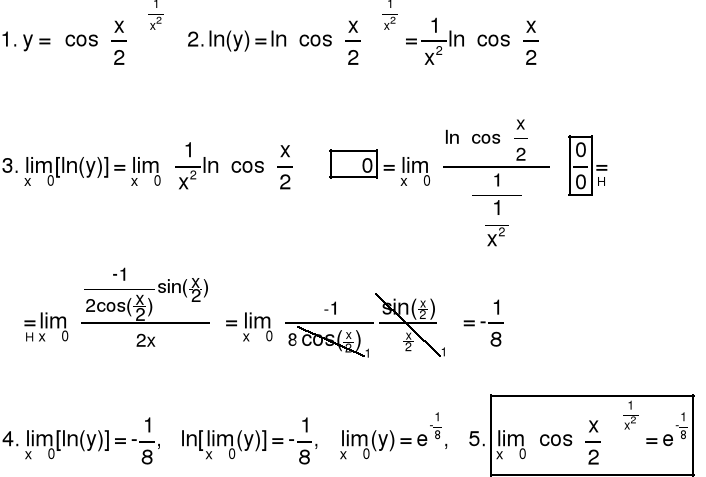
5.3 Twierdzenia o granicach nieoznaczonych

Obliczanie granic dla symbolu ∞⁰

Przykład 1 Obliczyć granicę funkcji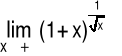

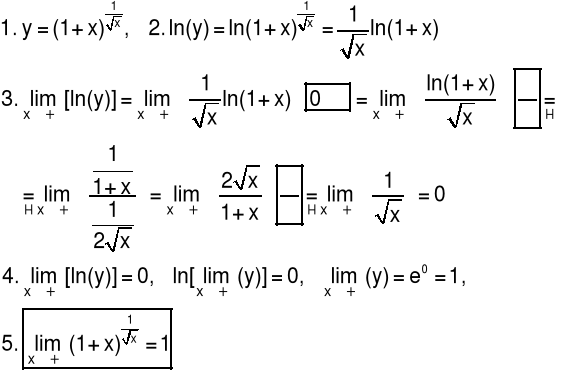
Przykład 2 Obliczyć granicę funkcji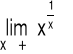

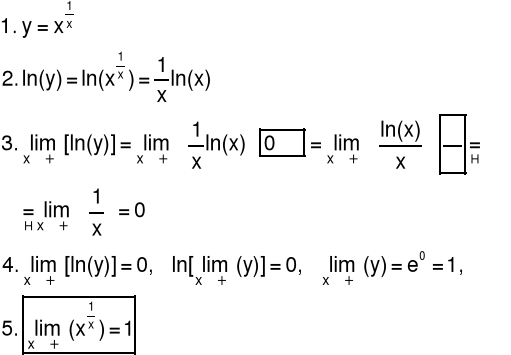
Guillaume François Antonie de L'Hôspital (1661-1704), matematyk francuski.