(6.72)

będącą warunkiem istnienia rozwiązania zagadnienia. Zależność ta jest nazywana związkiem dyspersyjnym , gdyż wyraża dyspersyjny charakter ruchu falowego, polegający na uzależnieniu prędkości fali

(6.73)

od jej długości.

W granicznym przypadku dla bardzo głębokiej wody
do-stajemy

(6.74)

natomiast dla bardzo płytkiej wody
jest

(6.75)

zatem ruch falowy występujący na powierzchni wody głębokiej odznacza się dużą dyspersją
a na wodzie płytkiej dyspersja nie występuje (c = const).

ĆWICZENIA

Przykład 6.1. Zbadać przepływ, którego pole prędkości określają składowe

Jest to przepływ nieściśliwy, o czym łatwo można się przekonać sprawdzając warunek ciągłości przepływu (6.2)

Jest to również przepływ potencjalny, gdyż znika składowa wektora
normalna do płaszczyzny przepływu

Potencjał prędkości znajdujemy wykorzystując równania:

po scałkowaniu mamy

Funkcję prądu wyznaczamy z równań (6.7):

Całkujemy pierwsze z tych równań

i następnie różniczkujemy względem x

wynika stąd, że

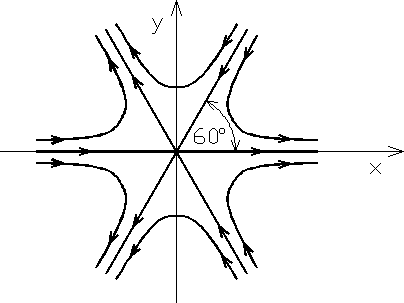
Rys. 6.21

Funkcja prądu jest zatem określona równaniem

obraz linii prądu dla
przedstawiony jest na rys. 6.21.

Widzimy więc, że rozważane pole prędkości może być wykorzystane do opisu przepływu w pobliżu naroży, których kąty załamania wynoszą 60°.

Przykład 6.2. Jaka zależność musi zachodzić pomiędzy stałymi a i b, aby równanie

określało potencjał prędkości. Ponadto dla otrzymanego potencjału wyznaczyć:

a) funkcję prądu,

b) moduł wektora prędkości

Funkcja
jest potencjałem prędkości, jeżeli spełnia równanie La-place'a:

czyli

stąd

Wobec powyższego

a. Po scałkowaniu zależności

otrzymamy

Również

zatem

Z przeprowadzonej analizy wynika, że

czyli

przeto równanie rodziny linii prądu będzie miało następującą postać

b. Składowe wektora prędkości wynoszą:

stąd

Przykład 6.3. Pole prędkości płaskiego przepływu płynu doskonałego określają składowe wektora prędkości:

.

Sprawdzić, czy przepływ jest potencjalny (niewirowy), wyznaczyć potencjał prędkości oraz funkcje prądu, a także określić kształt linii prądu i linii ekwipotencjalnych.

Przepływ potencjalny, czyli niewirowy, musi spełniać następujący warunek

Dla danych składowych wektora prędkości mamy:

,

a zatem spełniony jest warunek niewirowości przepływu.

W celu wyznaczenia potencjału prędkości skorzystamy z poniższego równania

skąd po scałkowaniu jest

Różniczkując funkcję ϕ względem x, otrzymujemy

z czego wynika, że

czyli

W związku z tym, potencjał prędkości

Funkcję prądu wyznaczymy z następującego równania

z którego po scałkowaniu mamy

Różniczkując ostatnie wyrażenie względem y, otrzymujemy

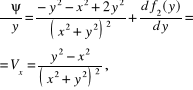
zatem

wówczas

stąd uzyskujemy zależność dla funkcji prądu

Równanie rodziny linii prądu wyznaczymy podstawiając
wobec tego

a po przekształceniu

Otrzymane tym sposobem wyrażenie jest równaniem rodziny okręgów o promieniu r, których środki leżą w punktach: (0, r), (0, − r) - rys. 6.22.

Linie ekwipotencjalne = const jako ortogonalne do linii prądu = = const są również okręgami, których środki mają współrzędne: (r, 0), (− r, 0).

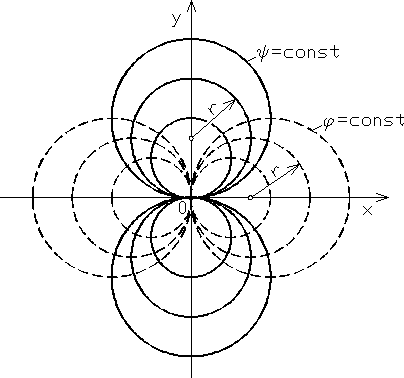
Rys. 6.22

Przykład 6.4. Wyznaczyć przepływ cieczy doskonałej, będący superpozycją przepływu jednorodnego z prędkością  U  równoległą do osi rzeczywistej, źródła znajdującego się w punkcie:
y = 0 oraz upustu znajdującego się w punkcie: x = a, y = 0 (rys. 6.9).

Uogólniając wzór (6.27) zapisujemy potencjał zespolony wytworzonego przepływu w postaci

i wyznaczamy funkcję prądu

Współrzędne punktów spiętrzenia
wynikają z równania

i określone są wzorami

Jeśli przyjmiemy

wtedy będzie

Funkcja prądu ψ = 0 pokrywa się z osią x dla oraz ; między punktami spiętrzenia jest określona równaniem

Równanie to opisuje krzywą symetryczną względem obu osi; musi być ona linią zamkniętą , gdyż w nieskończoności przepływ jest prądem jednorodnym.

Przykład 6.5. Funkcja
gdzie C = const ≠ 0, jest poten-cjałem prędkości płaskiego, ustalonego ruchu płynu doskonałego. Określić funkcję prądu oraz potencjał zespolony

W pierwszej kolejności sprawdzamy, czy funkcja

może być potencjałem prędkości, tzn. czy spełnia równanie Laplace'a:

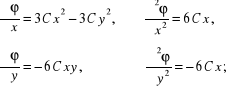
stąd

Uwzględniając zależność

otrzymujemy

skąd po scałkowaniu względem y

Po obliczeniu pochodnych:

z zależności

dostajemy

czyli

przeto

W związku z powyższym stwierdzeniem, funkcję prądu możemy przedstawić w na-stępującej postaci

Z definicji potencjału zespolonego

156

---