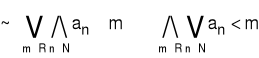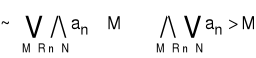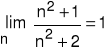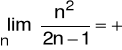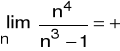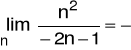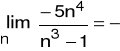II. ciągi liczbowe

2.1 Podstawowe określenia

Definicja (Ciąg liczbowy)

Ciągiem liczbowym nazywamy funkcję odwzorowującą zbiór liczb naturalnych w zbiór liczb rzeczywistych:

(2.1.1)

Sposoby określania ciągu liczbowego:

• Wzór

• Rekurencja

	- ciąg arytmetyczny
	- ciąg geometryczny
	- ciąg Fibonacciego^1

• Opis

an	to n-ta cyfra po przecinku w rozwinięciu dziesiętnym liczby π
bn	to n-ta liczba pierwsza
cn	to przedostatnia cyfra rozwinięcia dziesiętnego liczby (n+3)^2

• Wykres

• Tabela 1 → 1 2 → 1 3 → 2 4 → 3 5 → 5 6 → 8 7 →13 ...

• Podanie kilka początko-wych wyrazów ciągu: - liczb Fibonacciego^1 {1, 1, 2, 3, 5, 8, 13, ...} - liczb parzystych {2, 4, 6, 8, 10, 12, ...} - liczb nieparzystych {1, 3, 5, 7, 9, 11, ...}

¹ Leonardo Pisano Fibonacci (ok.1170 - ok.1250), matematyk włoski.

2.1 Podstawowe określenia

Definicja: (Ciąg ograniczony z dołu)

Ciąg {a_n} jest ograniczony z dołu, jeżeli zbiór {a_n} jest ograniczony z dołu, tzn.

(2.1.2)

Ciąg ograniczony z dołu

Definicja: (Ciąg ograniczony z góry)

Ciąg {a_n} jest ograniczony z góry, jeżeli zbiór {a_n} jest ograniczony z góry, tzn.

(2.1.3)

Ciąg ograniczony z góry

2.1 Podstawowe określenia

Definicja: (Ciąg ograniczony)

Ciąg {a_n} jest ograniczony z góry, jeżeli zbiór {a_n} jest ograniczony z góry, tzn.

(2.1.4)

Zbiór ograniczony

Przykłady:

Wyraz ogólny	Ciąg	Ograniczoność
		z dołu
		z góry
		ograniczony

Definicja: (Ciąg nie jest ograniczony z dołu)

Ciąg {a_n} nie jest ograniczony z dołu, jeżeli

(2.1.5)

Definicja: (Ciąg nie jest ograniczony z góry)

Ciąg {a_n} nie jest ograniczony z góry, jeżeli

(2.1.6)

2.1 Podstawowe określenia

Definicja: (Ciąg rosnący)

Ciąg {a_n} jest rosnący, jeżeli

(2.1.7)

Ciąg rosnący

Definicja: (Ciąg niemalejący)

Ciąg {a_n} jest niemalejący, jeżeli

(2.1.8)

Ciąg niemalejący

2.1 Podstawowe określenia

Definicja: (Ciąg malejący)

Ciąg {a_n} jest malejący, jeżeli

(2.1.9)

Definicja: (Ciąg nierosnący)

Ciąg {a_n} jest nierosnący, jeżeli

(2.1.10)

Definicja: (Ciąg stały)

Ciąg {a_n} jest stały, jeżeli

(2.1.11)

Uwaga:

• Ciągi rosnące i malejące nazywamy ściśle monotonicznymi, a ciągi nierosnące i niemalejące nazywamy słabo monotonicznymi.

• Monotoniczność dowolnego ciągu {a_n} możemy ustalić badając znak różnicy a_n+1 - a_n, a ciągu {b_n} o wyrazach dodatnich porównując iloraz b_n+1/b_n z liczbą 1:

an+1 - an		Ciąg
> 0	> 1	rosnący
< 0	< 1	malejący
≥ 0	≥ 1	niemalejący
≤ 0	≤ 1	nierosnący

2.1 Podstawowe określenia

Przykład 1 Zbadać monotoniczność ciągu:

(∗)

Badamy znak różnicy: a_n+1 − a_n

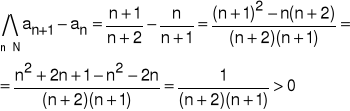
Wniosek: Ciąg określony wzorem (∗) jest rosnący.

Przykład 2 Zbadać monotoniczność ciągu:

(∗∗)

Badamy znak różnicy: b_n+1 − b_n

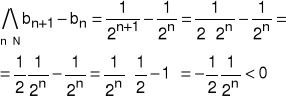
Wniosek: Ciąg określony wzorem (∗∗) jest malejący.

II. ciągi liczbowe

2.2 Granice ciągów

Definicja: (Granica właściwa ciągu)

Ciąg {a_n} jest zbieżny do granicy właściwej g∈R, co piszemy

(2.2.1)

wtedy i tylko wtedy, gdy

(2.2.2)

Granica właściwa ciągu

Twierdzenie: (O jednoznaczności granicy ciągu)

Każdy ciąg zbieżny ma dokładnie jedną granicę.

(2.2.3)

Przykłady:

2.2 Granice ciągów

Przykład: Wykazać z definicji granicy ciągu, że

Dowód: Mamy rozwiązać nierówność

względem n. Zatem:

Dla n>666 prawie wszystkie wyrazy ciągu należą do przedziału (-1-0,001; -1+0,001) ⇔ (-1,001; -0,999)

Uwaga: Wyrażenie „prawie wszystkie wyrazy ciągu” znaczy wszystkie wyrazy ciągu z wyjątkiem skończonej liczby wyrazów.

2.2 Granice ciągów

Definicja: (Granica niewłaściwa ciągu)

Ciąg {a_n} jest zbieżny do granicy niewłaściwej +∞, co zapisujemy

(2.2.4)

wtedy i tylko wtedy, gdy

(2.2.5)

Granica niewłaściwa +∞

Przykłady:

2.2 Granice ciągów

Definicja: (Granica niewłaściwa ciągu)

Ciąg {a_n} jest zbieżny do granicy niewłaściwej -∞, co zapisujemy

(2.2.6)

wtedy i tylko wtedy, gdy

(2.2.7)

Granica niewłaściwa -∞

Przykłady:

2.2 Granice ciągów

Przykład: Wykazać z definicji granicy ciągu, że

Dowód: Mamy rozwiązać nierówność

względem n. Zatem:

co kończy dowód.

Przykład:

Dla n>5 prawie wszystkie wyrazy ciągu są mniejsze od -27.

2.2 Granice ciągów

Przykład: Wykazać z definicji granicy ciągu, że

Dowód: Mamy rozwiązać nierówność

względem n. Zatem:

co kończy dowód.

Przykład:

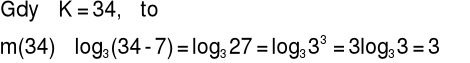
Dla n>3 prawie wszystkie wyrazy ciągu są większe od 34.

---