082

Granica ciągu liczbowego

pod uwagę pierwiastek

I 16/r + 1 oc” lim —;—-— = — = lim

łt->x \j fl    „OC /j-ko \

16n^2 n^1 2	1 n^2
ir	7
— +	—
rr	ir

= lim

/,-»•/-! i    7

1 + —

16 0 _L

116+ 4r

^ = Vl6 = 4

Odpowiedź

lim a = 4

n

ZADANIE 25

1 - 27/r

8 n² + 1

l — 27/?²    cc”

■ = — = lim

8«^: + 1 „cc „_>*

i

V

L ²¹jl

n² rr

= lim

— -27 /r

-2J_

8

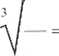
27    3

8 2

8/r _| 1

n- ir

i

«

\

₈₊a

rr i i 8 0

Odpowiedź

lim ci =--

»    9

ii—yjrj    Ł

ZADANIE 26

Znajdź granicę a = \n +10- -Vn.

82

1

Znajdź granicę a_t: =\ Rozwiązanie:

Najpierw zajmujemy się granicą ciągu, która znajduje się pod pierwiastkiem

2

- 27n-8/?² + 1