CCF20090513017

I. Indukcja i wyjaśnianie

2.4. Niektóre inne trudności probabilizmu

Probabilizmowi zarzuca się między innymi, że nieadekwatnie ujmuje praktykę naukową. Uczeni ani nie dokonują oceny stopnia potwierdzenia hipotez za pomocą metod Carnapa, ani nie kształtują stopnia własnego przekonania o trafności hipotez za pomocą reguły warunkowania. Zarzut ten nie jest bardzo poważny. Celem bowiem metodologii w ogóle, a teorii metody indukcyjnej w szczególności, nie jest opis metod faktycznie stosowanych przez uczonych, podobnie jak na przykład celem uprawiania logiki nie jest opis rzeczywistych procesów rozumowania. Logika zajmuje się raczej rekonstrukcją idealnych, normatywnych wzorców rozumowania. Zarówno program Carnapa, jak i bayesianizm dążą do zrekonstruowania czegoś, co zgodnie, aczkolwiek niekoniecznie trafnie, nazywają logiką nauki, czyli teorią idealnych wzorców postępowania naukowego w zakresie oceny wartości poznawczej hipotez.

Poważniejszym problemem jest kwestia oceny hipotez uniwersalnych. W logikach Carnapa, o czym była mowa wyżej, stopień potwierdzenia dowolnej hipotezy uniwersalnej przez jakiekolwiek świadectwo (zdanie szczegółowe) jest równy zero. Tymczasem wysuwanie i sprawdzanie hipotez uniwersalnych, to jest hipotez tej treści, że każdy obiekt x określonego rodzaju zachowa się w sposób Z, ilekroć zajdą warunki IV, symbolicznie (Vx)[W(x) -* Z(x)], należy do istoty działalności naukowej. Nic dziwnego, że program Carnapa doczekał się korekty, która miała wyrównać jego rzekomy niedostatek. Jaakko Hintikka³³ sformułował uogólnienie metod Carnapa, tak zwane dwuwymiarowe kontinuum metod indukcyjnych, w których hipotezy uniwersalne mogą mieć dodatni stopień potwierdzenia.

Sam Carnap zerowego stopnia potwierdzenia hipotez uniwersalnych nie uważał za mankament proponowanych przez siebie rachunków logicznych. Sądził, że metody indukcyjne są przede wszystkim narzędziem oceny stopnia wiarygodności przewidywań. U podłoża takiego stanowiska tkwi instrumentalizm, to jest pogląd, wedle którego hipotezy uniwersalne nie są zdaniami kandydującymi do miana prawdziwych lub fałszywych, lecz regułami wyprowa-

^,s Zob. J. Hintikka, A Two-DimensionalContinuum oflnductłve Methods, w: Aspects of lnductive Logic, red. J. Hintikka, P. Suppes, Amsterdam 1966.

2. Nauka jako wiedza prawdopodobna

Metoda

Bayesiańska jest nieprzydatna do dyskryminacji hipotez teoretycznych

dzania przewidywań ze zdań opisujących warunki początkowe eksperymentu. Niezależnie od oceny instrumentalizmu, którą zajmiemy się w rozdziale IV, wypada zaznaczyć, że z punktu widzenia przeprowadzonej wyżej analizy, w myśl której probabilizm prowadzi do regresu w nieskończoność, wstrzemięźliwość Carnapa w kwestii oceny hipotez uniwersalnych przedstawia się dalekowzrocznie. Z uwagi na regres w nieskończoność metody probabilistyczne należy uznać za niesamodzielne, to znaczy mechanizm ocen probabilistycznych nie może wystartować bez wcześniejszego założenia pewnych hipotez. To stawia pod znakiem zapytania zdolność probabilizmu do sformułowania metody oceny hipotez uniwersalnych. Nic jednak nie stoi na przeszkodzie, by zakładając pewne hipotezy - w logikach Carnapa są nimi hipotezy na temat statystycznej zależności zdarzeń - dokonywać na ich podstawie, metodami probabilistycznymi, ocen prawdopodobieństwa spełnienia się określonych przewidywań. Wydaje się, że tego rodzaju postępowanie w nauce jest dość typowe. Na przykład na podstawie pewnych hipotez można oceniać prawdopodobieństwo spełnienia się prognozy meteorologicznej.

Omawiając bayesianizm jako alternatywne wobec programu Carnapa podejście probabilistyczne, skoncentrowałem się na trudnościach doboru świadectwa do zastosowania we wzorze Bayesa, pominąłem zaś kwestię oceny hipotez uniwersalnych. Teraz pora to przemilczenie nadrobić. Historia nauki odnotowała liczne eksperymenty dokonywane przez bai'dzo młodych uczonych, polegające na upuszczaniu rozmaitych drobnych przedmiotów z balkonu. Pytanie brzmi: która to hipoteza uniwersalna zyskała potwierdzenie kosztem niejednego uszczerbku zasobów sreber rodowych? Przypuśćmy, że jest nią prawo powszechnego ciążenia:

Na mocy reguły warunkowania, zaginięcie każdej łyżeczki podwyższa prawdopodobieństwo trafności domysłu Newtona, zgodnie z wzorem:

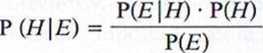
P(£ | H) • P(H)

P(E|H) • P(//) + P(£|-itf) • P(-■//) ’