Xerox Phaser200MFP 081126112658

66 Janusz Buga, Helena Kassyk-Rokicka

Rozwiązanie

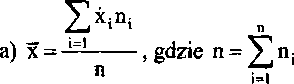
x =-= 3,06 tys. zł

100

Uwaga: wagami w powyższym rozwiązaniu były liczby studentów odpowiadające poszczególnym poziomom oszczędności. Zamiast liczbami studentów można posłużyć się częstościami względnymi. Wynik otrzymany wówczas będzie identyczny z wynikiem uzyskanym w punkcie a, czyli 3,06 tys. zł. Zalecamy przeprowadzenie odpowiednich rachunków.

b) obliczamy przeciętny poziom oszczędności za pomocą miar po-zycyjnych. Zaczynamy od wyznaczenia dominanty Do. Musimy skorzystać ze wzoru interpolacyjnego (2.8):

Do = x_d +

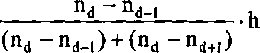
W rozpatrywanym przykładzie dominanta znajduje się w przedziale od 2,7 do 3,1, gdyż temu przedziałowi wartości cechy odpowiada największa liczebność (częstość).

Do = 2,7 +-—---

(30-20)+ (30+ 25)

• 0,4 = 2,7 + 0,06 = 2,76 tys. zł

c) wyznaczymy teraz wartość mediany (Me), czyli wartość kwartyla drugiego. Zastosujemy wzór (2.9) dla i = 2 (tzn. Q₂).

k-l

Me = x_fc +

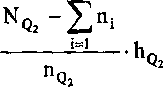
gdzie:

x_K - dolna granica przedziału, w którym znajduje się mediana,

k-1 - kolejny numer przedziału poprzedzającego bezpośrednio przedział z medianą.

Me = 2,7 + -° - 0,4 = 3,03 tys.zł 30

Z uzyskanych dotychczas wyników wiadomo, że dominanta oszczędności studentów wynosi 2,76 tys. złotych. Oznacza to, że najczęstszymi w tej grupie osób oszczędnościami były kwoty zbliżone do 2,76 tys. zł.

Natomiast oszczędności środkowe (wartość Me) wynoszą 3,03 tys. zł. Połowa oszczędzających studentów ma lokaty poniżej, a druga połowa powyżej 3,03 tys. zł.

d) obliczamy wartość kwartyla pierwszego (Qi). Korzystamy ze wzoru (2.9) dla i = 1.

Q,= 2,3 + ^~0,4 = 2,7 tys.zł

c) obliczamy warość kwartyla trzeciego (Q₃). Wzór (2.9) dla i = 3.

Q₃ - 3,1 + ^⁵- • 0,4 = 3,42 tys. zł

Wartość kwartyla pierwszego orzeka, że 25% studentów ma Oszczędności poniżej 2,7 tys. zł, natomiast 75% studentów ma oszczęd-iHiki powyżej 2,7 tys. zł.

'/, wartości kwartyla trzeciego wnioskujemy, że 75% studentów po-flUidn oszczędności poniżej 3,42 tys. zł, natomiast 25% studentów za-Ó^ezędziło kwoty powyżej 3,42 tys. zł.

W dalszym ciągu będziemy korzystali z treści i danych liczbowych jiMyklndu 2.6.6. Zbadamy obecnie stopień zróżnicowania oszczędności Wdfótl studentów. Zastosujemy w tym celu podstawowe miary, takie jak Mllyltylenie standardowe i współczynnik zmienności. Zgodnie ze wzo-