Xerox Phaser200MFP 081126114709

146 Janusz Buga, Helena Kassyk-Rokicka

14,0%, w 1999 r. w stosunku do 1998 r. wzrost o 17,4%, natomiast w roku 2000 w porównaniu z rokiem 1999 notujemy spadek sprzedaży samochodów o 25,3%. Inaczej mówiąc, poziom sprzedaży samochodów w 1998 r. stanowi 114% poziomu sprzedaży z roku poprzedniego, tj. 1997 r., a poziom sprzedaży w 1999 r. stanowi 117,4% liczby sprzedanych samochodów w 1998 r., natomiast w 2000 r. poziom ten stanowi tylko 74,7% poziomu sprzedaży, jaki miał miejsce w 1999 r.

Zauważmy, że interpretacja wyników indeksów prostych jest bardzo podobna do interpretacji wyników przyrostów względnych. Nie jest to przypadek, lecz wynik bezpośredniej zależności, jaka istnieje między tymi miernikami, a mianowicie: przyrost względny powiększony o 1 daje indeks prosty (indeks prosty pomniejszony o 1 daje w wyniku przyrost względny). Ostatnie dwie kolumny tablicy 3 ilustrują omawianą zależność. Zwracamy uwagę, że przy spadku poziomu zjawiska przyrost stosunkowy jest liczbą ujemną, co ma miejsce w omawianym przykładzie dla roku 2000. Jeżeli wskaźniki są ujęte w procentach, musimy je powiększać lub pomniejszać o 100.

W praktyce często będziemy dążyli do ustalenia średniego tempa zmian w poziomie zjawiska przypadającego na jednostkę czasu w badanym szeregu czasowym. Wskaźnik średniego tempa obliczamy w dwóch etapach, korzystając z prostych indeksów łańcuchowych. W etapie pierwszym liczymy średni indeks łańcuchowy³³:

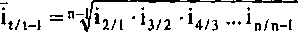
(5.10)

gdzie, przypomnijmy, t = 1, 2, 3, n i jest numeracją kolejnych jednostek czasu (okresów lub momentów) w badanym szeregu czasowym.

W etapie drugim obliczamy średni wskaźnik tempa:

(5.11)

T = i,„-,-1,00

³³ Znajduje tu zastosowanie średnia geometryczna, którą definiuje się następująco: średnia geometryczna jest to pierwiastek k-tego stopnia z iloczynu „k” wyrażeń pod pierwiastkiem.

lub w ujęciu procentowym:

T=(I_t/t__Ł -100)-100.    (5.12)

Etapy obliczeń zilustrujemy przykładem zaczerpniętym z tabl. 2.

Tabl. 4. Wydatki na ochronę zdrowia

Lata	t	Wydatki w zł na osobę	i - ^yt
1996	1	433,3
1997	2	488,7	1,128
1998	3	540,4	1,106
1999	4	588,9	1,090
2000	5	620,2	1,053

Źródło: Obliczenia własne

Średni wskaźnik łańcuchowy dla przykładu: wydatki na ochronę zdrowia w latach 1996-2000 (n = 5 lat), wynosi:

I_t/w = VU28-1,106 1,090 1,053 s 1,094;

1,094 • 100 = 109,4%,

Stąd średni wskaźnik tempa zapiszemy:

T = 1,094 -1,00 = 0,094;

T= 109,4-100,0 = 9,4%.

Otrzymany wynik ma jasną, logiczną interpretację. Oznacza on, że w latach 1996-2000 średnie roczne tempo wzrostu wydatków na ochronę zdrowia w Polsce liczonych na 1 osobę w zł wynosiło 9,4%. Innymi