0108

110
IX. Całka oznaczona
wyjdziemy z formalnie obliczonej funkcji pierwotnej
—— arc tg
3x(x2—1) x*—4x2+l
i podstawimy tu x = 0 i x = 1, to otrzymujemy dla całki paradoksalną wartość 0 (przecież całka funkcji dodatniej nie może być równa zeru!).
Błąd tkwi w tym, że podana funkcja pierwotna ma skok dla x = xQ. Jeśli obliczymy oso
bno całki od 0 do x0 i od x0 do 1, to otrzymamy prawidłowy wynik
1
O
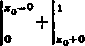
TT
3 •
11) Za pomocą funkcji pierwotnych łatwo można obliczyć całki
J
2
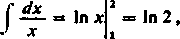
1
dx
l + x2
i
arc tg x
o
Tt_
4 '
Z uwagi na to, że całki te są granicami odpowiednich sum całkowych, możemy otrzymać na przykład takie wzory graniczne:
ii™(iir + dT+"+ir) = In2’
310. Inne wyprowadzenie wzoru podstawowego. Udowodnimy teraz wzór podstawowy (A) przy ogólniejszych założeniach. Niech funkcja f(x) będzie całkowalna w przedziale b} i niech funkcja F(x), ciągła w tym przedziale, ma pochodną równą /(*):
(3) F'(x) =/(x)
w całym przedziale otwartym (a, b), albo nawet tylko wszędzie z wyjątkiem skończonej liczby punktów.
Rozbijmy przedział <a, b} na części za pomocą punktów
x0 = a < Xi < x2 < ... < xt < x,+! < ... < x„ = b
troszcząc się tylko o to, by wśród tych punktów znalazły się wszystkie te punkty, w których nie jest spełniony warunek (3), jeśli takie punkty istnieją. Mamy oczywiście
F (b) - F (a) = [F (xi+1) - F (xf)].
i-O
Wyszukiwarka
Podobne podstrony:
98 IX. Całka oznaczona 10“ Uogólnione twierdzenie o wartości średniej. Zakładamy, że 1) funkcje /(x)
100 IX. Całka oznaczona Ciągłość funkcji fU) w punkcie t — x oznacza, że do każdej liczby e > 0 m
102 IX. Całka oznaczona — jak to widać z założeń o funkcji /(x) są nieujemne, więc zastępując
104 IX. Całka oznaczona Podstawiąjąc wartości funkcji w lewych końcach przedziałów, otrzymujemy
116 IX. Całka oznaczona Uwaga. Zwróćmy uwagę na ważną właściwość wzoru (9). Przy obliczaniu całki
140 IX. Całka oznaczona przyjmuje w punktach z = a, (a+ó)/2, b te same wartości co i funkcja/(z). Ła
całka nieoznaczona Całka nieoznaczona to ogólna postać funkcji pierwotnej funkcji. Całkę nieoznaczon
82 IX. Całka oznaczona W każdym z odcinków <*,, x,+i> wybierzmy dowolny punkt x = Ę, (l): X
84 IX. Całka oznaczona Sumy Darboux mają następujące, proste własności: Własność 1. Jeśli do
86 IX. Całka oznaczona e > 0 można znaleźć taką liczbę ó > 0, że skoro tylko X < 5 (tzn. je
88 IX. Całka oznaczona Dla pierwszej sumy, podobnie jak w poprzednim twierdzeniu, mamy < e(b-a).
90 IX. Całka oznaczona Łatwo zauważyć że nie wywoła to zmiany wartości samej całki. Wynika to stąd,
92 IX. Całka oznaczona Przyjmijmy teraz i _ « 2m Q ’ gdzie 12 oznacza oscylację
94 IX. Całka oznaczona 303. Własności całek wyrażające się równościami. Podamy dalsze własności
96 IX. Całka oznaczona więc analogicznie w przedziale <at, bf> możemy znaleźć podprzedział
106 IX. Całka oznaczona 308. Podstawowy wzór rachunku całkowego. Widzieliśmy już w ustępie 305, że d
108 IX. Całka oznaczona Ponieważ poszczególne składniki łatwo jest scałkować według wzoru (A), mamy
112 IX. Całka oznaczona napisać analogiczny wzór dla całek oznaczonych (5) J f(x)
114 IX. Całka oznaczona W analogiczny sposób sprawdza się pozostałe wzory. 3) Znaleźć całki n/2
więcej podobnych podstron