0464

466

XII. Ciągi i szeregi funkcyjne

Jeżeli weźmiemy na przykład

F(y)-e>- l+JS’

m»l

to okazuje się, że

_cAu>-.t, °| I \^a* I °‘l    ¹    | f |    2g| I °I 1    ¹    |-    +U₊ I °r1 I I

jr L 1!    2! J x² t I! 2!    3! J jc» " LI! " n\ J x" "

Ciekawym zastosowaniem tego twierdzenia o podstawianiu szeregu do szeregu jest (podobnie jak w przypadku zbieżnych szeregów potęgowych, 448) dzielenie rozwinięć asymptotycznych funkcji B(x) i A (x) przy założeniu, że wyraz wolny a₀ drugiego z nich jest różny od zera. Ponieważ w porównaniu z ustępem 448 nie trzeba tu używać żadnych nowych idei, nie będziemy się na tym zatrzymywali.

4° Przejdźmy do całkowania rozwinięcia asymptotycznego.

Niech funkcja A (jr) będzie ciągła w przedziale X — (a, + «o)./ ma rozwinięcie asymptotyczne

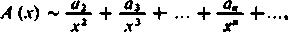
(13)

rozpoczynające się od wyrazu zawierającego \/x². Istnieje wtedy skończona całka tej funkcji w granicach od dowolnego x >a do -(-ooC) i całka ta, jako funkcja x, ma rozwinięcie asymptotyczne

(14)    f A (.r) dx ~ -22- + SLł-. -L-4- ... ą--2s_.    +- —

^J    x 2    x²    n— I x"-‘

X

które otrzymujemy z rozwinięcia (13) całkując je w sposób formalny wyraz za wyrazem.

Rzeczywiście, przyjmując, że

A,

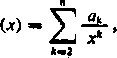
r,(x) = A (x)—A„(x),

mamy dla dowolnie obranego e>0 i dowolnego ustalonego n (15)    Jf"|r,(jr)| < e ,

jeżeli tylko x będzie dostatecznie duże.

Jeżeli X>x, to

XXX    n    .    X

J A (x) dx = J A,(x) dx+ J r„(x) dx -    \—^ZT ~    + J ^r"W ^dx■

x    xx    k«2    x

Dla X oo otrzymujemy

(16)    / A (x) dx = -Hi- • ± +    • -L + ... + -2ł_. —L- +*._,(,),

^J    i x 2 x²    «—I

gdzie

X    co

R»-i(x) = lim f r„(x) dx = J' r„(x) dx.

X

(') Przypominamy [patrz str. 244], że całką funkcji f(x) w granicach od a do + oo nazywamy granicę

+ 00    A

J f{x) dx —■ lim J f(x) dx .

a    a