0600

602

XIV. Całki zależne od parametru

Pozostaje obliczyć całkę f e~^x2x¹'^,dx — /„. Całkując przez części wyprowadzamy z łatwością wzór o

redukcyjny

stąd

»    2    ¹    2^V+I

Podstawiając ten wynik do znalezionego rozwinięcia otrzymujemy

J e~¹ cos 2bx dx = ¹ ^ +

2 l Zj »! J 2

(b) Odpowiedź:.

(c) Analogicznie otrzymujemy rozwinięcie

00    3Ł

/ ^e'^{xl sin 2 (-26V}‘¹ •

l(2r-l)!!

które do „skończonego” wzoru nie prowadzi. Później na innej drodze zbadamy własności nowej — już nieelementarnej — funkcji, za pomocą której można by było przedstawić tę całkę [523, 5) (b)].

7) Znaleźć wartość całki

- dx

W

(³ == 1, 2, 3,...).

Rozwiązanie. Rozwijamy funkcję

-1    1-e-

w szereg geometryczny i po pomnożeniu przez x^lt~^l otrzymujemy szereg

~.2³-l    ®

^x__ y _Xlk-i_e-2³nx

e^m3-l

Wyrazy tego szeregu są dodatnie i jest on zbieżny jednostajnie w dowolnym przedziale <t], A} (0 <i}<A< < + oo). Ponieważ suma tego szeregu jest przy tym całkowalna w przedziale od 0 do + oo, więc możemy go całkować wyraz za wyrazem (³). A więc

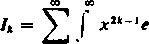
a-l 0

2,n,_dx _ V (2k-iy. ₌ C2A-1): y Z_i (2mr)“    (27t)“ Z_i

1

rt

2 k '

Wprowadzimy tu liczby Bemoulliego B_k [449]. Przypominamy, że

B_k - ²'^)^! V-L (27t)“ Zj

1

(2w)! = (2v)!!(2v-l)!! = 2V(2³-1)!!

2

(^ł) W tym i następnym zadaniu korzystamy jednocześnie z twierdzeń 1 i 1' z poprzedniego ustępu stosując je odpowiednio do przedziałów <1, + oo) i <0,1>.

3

Posłużyliśmy się tu oczywistą równością