0654

656

XIV. Całki zależne od parametru

3) Obliczyć całki

(a) f    ......^XT:' dx {a, b,p> 0),

J (x+p)'+^b

o

Wskazówki, (a) Podstawienie y — (l+/>)

(b) j

(l+x²)^m+’

dx

x    1

—■—. (b) Podstawienie u — — > x+p    2

(w, n > 0).

(1+Jc)² l+x² '

Odpowiedź, (a)    '¹ _T R (g, 6);    (b) 2"^"^-2 B (m, //).

Stąd można otrzymać z kolei wiele interesujących całek. Na przykład w (b) przyjmiemy n = 1 — m, 2/h— 1 = cos 2a i podstawimy x tg <p, to otrzymamy

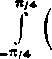
cos g»+sin q> cos <p—sin <p

^cos 2«

dtp =

_7t_

2 sin (n cos²a)

4) Obliczyć całki n/2

(a)    J sin*^-,ę) cos*^-1? dtp (a, b > 0);

o

tt(z    nu

(b)    | sin*-*y = J cos*~^,gptfę> (a > 0);

o    o

It/2

(c) f tg^c<pdq>    (|cl < 1) .

Rozwiązanie, (a) Podstawiając .v = sin tp sprowadzimy tę całkę do całki

korzystając teraz z zadania 1) dostaniemy

7%in*-Vcos»-V</*-J-WiL.l.) ,-L. i    2 U’ 2/    2 _r^n±6j

(b) W szczególności, dla b = 1, otrzymamy stąd

n/i

f sin‘~'<pd<p

GL

-    r(*±L)

Stosując wzór Legendre’a można przepisać ten wynik w postaci

J sin*^-'<p dtp = 2'

-2 ^ ( 2 )1    ₌ 2.-i_B (±

r(a)    \2’2/

(’) Łatwo jest sprawdzić, że w tym wzorze jako szczególne przypadki zawarte są obydwa wzory (8) z ustępu 312.