Image0084 BMP

Rn/wią/ntitr dl u obszaru na zewnątrz walca przyjmujemy w postaci

Rn/wią/ntitr dl u obszaru na zewnątrz walca przyjmujemy w postaci

(9.35)

A_l2~g(r)i>in0, r^r₀.

a po podstawieniu do równania (9.28) otrzymujemy jednorodne równanie różniczkowe Eulera

d ²g

da _i

dr

_dj,2 +r —-₅(r)=0,

(9.36)

którego rozwiązaniem jest

(9.37)

C₃

tf (»*) = — + C₄r, r

gdzie C₃, C₄ są stałymi całkowania. Potencjał wektorowy na zewnątrz walca wyraża się wzorem

A?z~

sinO,

(9.38)

Składowa indukcji magnetycznej w obszarze na zewnątrz walca wynoszą:

Br 2 =

Bez ⁼

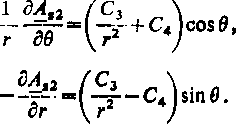
(9.39)

W bardzo dużej odległości od walca pole magnetyczne jest równomierne, wobec czego 3_r2^£₀co$ 0, gdy r-+oo. Na podstawie wzoru (9.39) znajdujemy B_rl-*C_A cos 8, gdy r-M», wskutek czego C₄ = B₀. Stale C_t, C₃ wyznaczamy na podstawie warunków brzegowych

Bj 1 |f = ro ⁼ Bf2 |r = r₀ »

B«t '■    _ B₆₂    (9.40)

P Jr*ro PO r=ro

które wyrażają ciągłość składowej normalnej indukcji magnetycznej i składowej stycznej natężenia pola magnetycznego w punktach powierzchni walca. Podstawiając zależności (9.33), (9.34) i (9.39) przy C_A=B₀ do wzorów (9.40), otrzymujemy równania:

Ci

— /j(kr ₀) cos 0 =

-C^o(fcr₀) + 7_a(kr₀)] sin 6= ~    -_si_n9,

|COS0,

z których wyznaczamy

_c =__⁴mb₀

‘ fc [(P + Po)Jo(kr₀) - (/; - fi₀)I_z(kr₀)) ’ _C =£ r2 (p-Poj/oCkrp)-^ +/r₀)J₂(kr₀)

³ ~° °(p +Po)^(^o) -(P~Po)^(kr,,) *

A,,_____•)/<»„ /,ar)sinO    ₍,.₄₁₎

k [(/t + /J₀) Io(kro) ~ (fi~ Po)¹2(*^f'o)]

Wyznaczymy gęstość prądu indukowanego w walcu, przy założeniu, że /z=/z₀; mamy / , , = - jo>A_I1, zaś gęstość prądu w walcu jest równa J_z—yE_Il. Po podstawieniu zależności l‘Ml) przy fi=/ł₀, otrzymujemy    *

₌ j2czy_:g₀f₁(kr)sine

fci₀(kr₀)

Zależność gęstości prądu od r charakteryzuje iloraz /_t(Ar)//₀(kr₀). Dla ilustracji przedstawiono w tabeli 9.2 moduł tej funkcji dla różnych |Ar| przy założeniu, że/ =50 Hz, y;- 56 ■ 10⁶ S/m, |Ar₀!=5; w rozpatrywanym przypadku mamy |A|=s/cofi^y—148,7 m“¹.

Tabela 9.2

\kr\		h(kr)		jAr|	| A(*r)
		/0(fcr0)			| /o(Aro) |
0	0			2	0,847
0,2	0,100			2,5	0,909
0.5	0,250			3	0.923
1	0,494			5	0,933
1,5	0,706

9.4. Zjawisko zbliżenia

Dwie nieskończenie długie i bardzo szerokie płyty są do siebie równoległe (rys. 9.5), a w każdej płycie płynie prąd sinusoidalny o wartości zespolonej /. Przyjmujemy, że zwroty prądów w płytach są przeciwne, a grubość d oraz odległość 2b obu płyt są bardzo małe

^Zt

Rys. 9,5. Dwie równoległe płyty przewodzące prąd 1