45433 img484

Najpierw zatem badamy przebieg zmienności funkcji f\\

1. D, = (O, 1) u (1, +oo).

Najpierw zatem badamy przebieg zmienności funkcji f\\

2. /, (x) = O o

x² - 4 x² - 1

= 0 a x e (0, 1) u (1, +oo)

<=> x - 2. Zatem

punkt wspólny wykresu funkcji z osią 0X to punkt (2, 0)'.

1 -

1 -

3. Obliczamy: lim fi (x) = lim

X-»+°°    X—>+co

= 1, skąd wynika, że istnieje

asymptota pozioma wykresu o równaniu y = 1 (prawostronna). W związku z tym nie ma potrzeby badania istnienia asymptoty ukośnej (prawostronnej). Następnie obliczamy lim ₊ /-,(x) = 4. Ponadto:

Ijm/r (x) = lim. ~ = +«, lim₊ (x) = lim₊ 2L—y = = -<»,

x—y 1    X—^ 1    _ "J    x—^ 1    X—^ 1    _ "j

I

o-

asymptotą pionową jest więc prosta o równaniu x =1. 6x

o⁺

4. /i'(x) = —--- (sprawdź!), Dy< = Dy. Widzimy, że równanie

(x ^— 1)

/,' (x) =0 jest sprzeczne w Dy -, ponadto dla każdego x e Dy, mamy /-,' (x) > 0.

5. Wstawiamy otrzymane wyniki do tabelki:

X	(0, 1)	1	(1.2)	2	(2,+oo)
//w	+	X	+	+	+
/iM	+00 4	X	—00	0	-1

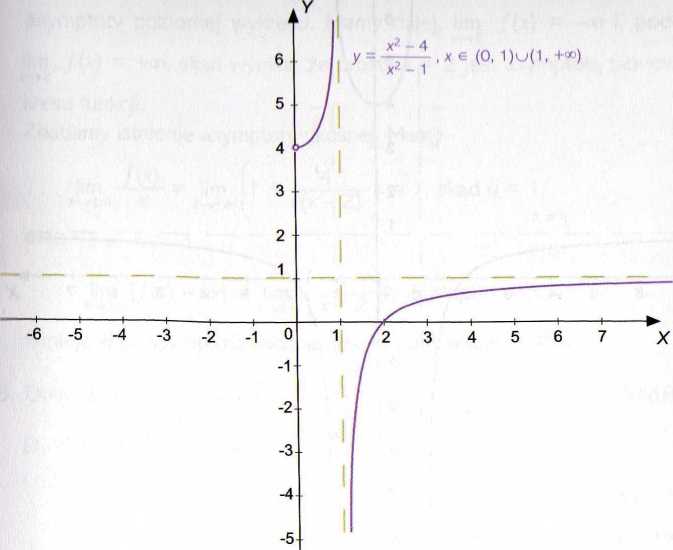
Obliczamy teraz /(O) = 4 i zauważamy, że w lewostronnym sąsiedztwie punktu x₀ = O funkcja / jest określona tym samym wzorem, co funkcja /i,więc w tym otoczeniu funkcja / jest ciągła i jej pochodne jednostronne są równe, ponieważ

lim /'(*) = lim

x-»0    x—>Cf

6x

(*²- 1)²

= O

Ponadto

x—>0

x-»0’

6x

*->o (x² - 1)'

= 0,

skąd wnioskujemy, że /'(O) = O. Zatem funkcja / jest różniczkowalna w punkcie x₀ = O, poza tym jest to punkt krytyczny. Teraz możemy już naszkicować wykres funkcji /: