114 2

226 X. Badanie przebiegu zmienności funkcji

zatem

dy dy dx 900e~ ^0,021 — 500    „    _{5 0 02f}

dx dt ‘ dt 800e^{_ 0,021    8    8} *

Obliczamy drugą pochodną; ponieważ

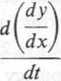
JL_0,02(

80^c

więc

d*y

dx²

. ^dX —Só^e°’⁰²' ₌ _ _J_ ^0.04,

dt ‘ dt 800e~⁰’⁰²'    64000

Moment największego wzniesienia pocisku znajdziemy rozwiązując równanie dyfdt=o (albo dyldx = 0), czyli

900<r^o,°²'-500 = 0,    skąd e"^0,02'= |

Aby rozwiązać to równanie, stosujemy logarytmy dziesiętne; otrzymujemy — 0,02f log e = log |-,    czyli    — 0,02f- 0,4343= -0,2553.

Stąd

' = 50~*29,4s.

Pozostaje do obliczenia wartość x = 40000(l —e^-0’⁰²'), gdzie e^_0,02' = |; otrzymujemy

x = 40000 (l-f) = 40000- | «17800 m.

Wreszcie

y= 45000-±-500-29,4 = 5300 m.

A więc pocisk osiągnie najwyższy poziom po upływie t = 29,4 s od momentu wystrzału w odległości poziomej 17800 m i na wysokości 5300 m.

Zadanie 10.57. Działo, którego lufa jest nachylona do płaszczyzny poziomej pod kątem a, wyrzuca pocisk z prędkością początkową v₀ (rys. 10.42). Znając przyśpieszenie

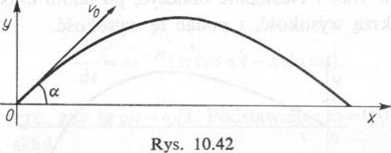
ziemskie g wyznaczyć kąt a, przy którym pocisk padnie na płaszczyznę poziomą ^{w oc}* ległości największej (oporu powietrza i działania wiatru nie bierze się pod uwag?)-

x = u₀cosa't,    y = v₀sinof t — ~gt²,

gdzie t oznacza czas liczony od momentu wystrzału.

Rozwiązanie. Aby znaleźć moment upadku pocisku na płaszczyznę poziomą, należy _f0Zvviązać równanie y=0, czyli

1    2    2t?₀

i>₀sina-r-jgf =0, skąd t-—sina.

g

wówczas odległość x wynosi

2v₀ sin a vl sin 2a

x = v₀ cos a-=-.

£    g

Jest rzeczą widoczną, że wartość x będzie największa, gdy sin 2a będzie największe, czy g^y sin2a = l, a to osiągniemy biorąc a=45°.

Zadania

Znaleźć ekstrema następujących funkcji oraz punkty przegięcia odpowiadających im krzywych (zad. 10.58- 10.69):

10.58. y = x³ + 12x²+36x —50.

10.60. y = x³—6x²+9x —2.

10.62. y=x³+x + l.

10.64. y = x⁴ —8x³+22x² —24x + 12.

10.66. y = xH—-.

x

10.68. j,    .

x² + l

10.59. y=2x³ —9x²—24x —12. 10.61. y= — x³ +x².

10.63. y = x (3 — x)².

10.65. y=x⁵ —5x⁴+5x³ + l.

, 1

10.67. y=x² + -= x

10.69. y = xV4-x².

10.70.    Wykazać, że krzywda y{x² +a¹) = a²(a — x) ma trzy punkty przegięcia leżące na jednej prostej.

10.71.    Dobrać a tak, aby krzywa y=x³+ax² + l miała punkt przegięcia przy x=l.

10.72.    Zbadać, przy jakiej wartości a krzywa y = x⁴+ax³ + § x² +1 będzie wklęsła.

Znaleźć ekstrema następujących funkcji i równania asymptot odpowiadających im ^krzywych (zad. 10.73 -10.81):

10.73.	x 2 y = -+-. 2 x	10.74.	2x + l x—4'
10.75.	6x	10.76.	x^2 —3x+2
	x^2 + 2x+4‘		* x^2+3x+2
!0.77.	x^2+x-l	10.78.	x^3+x
	^J x^2-.v+r		^x^4+x^2+l