23 luty 07 (94)

Jeżeli moduł przełożenia kierunkowego j/£_bj > 1, wówczas przekładnia służy do redukcji prędkości kątowej i jest nazywana reduktorem.

Jeżeli moduł przełożenia kierunkowego \ig_b\ < 1, wówczas przekładnia służy do zwiększania prędkości kątowej i jest nazywana multiplikatorem.

Przełożenie przekładni można wyrazić za pomocą parametrów geometrycznych kół, uwzględniając podstawową zależność

v_o = (0 |    (2.34)

gdzie:

v₀ - liniowa prędkość obwodowa wspólna dla obydwu współpracujących

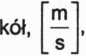
d - średnica podziałowa koła zębatego lub średnica koła tocznego, [m], co - prędkość kątowa koła, [s~*].

Jeżeli chcemy wyrażać przełożenie za pomocą prędkości obrotowej n, to na-

leży dodatkowo uwzględnić zależność: co =    [^s 11 gdzie n

obr.

min

Po uwzględnieniu związku (2.34) wzór na przełożenie przekładni zwykłej przyjmuje postać

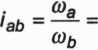
Hł

n_b

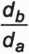
(2.35)

W przypadku przekładni zębatych, biorąc pod uwagę ich podstawowe cechy geometryczne, wzory na przełożenie możemy wyrazić również jako stosunki odpowiednich liczb zębów. Zależności geometryczne i kinematyczne dla przekładni zębatej o zazębieniu zewnętrznym przedstawia rysunek 2.33. Analogiczne zależności dla przekładni zębatej o zazębieniu wewnętrznym przedstawia rysunek 2.34.

Podstawowe zależności geometryczne i kinematyczne, wspólne dla obydwu rodzajów przekładni:

moduł zazębienia

t

m = —

71

(2.36)

średnica podziałowa

d =

zt

n

zm

(2.37)

92