314 2

314

7. Różnice skończone w całkowaniu i różniczkowaniu

Dokładniejsze wzory przybliżone można też otrzymać, posługując się techniką opera, torową i opierając się na operatorowym wyrażeniu rozwinięcia Taylora (zob. twierdzenie 7.6.1):

/ c d\

(7.7.12)    u(x₀ + h. jf₀^A)=exp(^—+•*—JuU₀. y₀)

Zob. też zadanie 7 do § 7.7.

Dla obszarów różnych od prostokąta siatkę prostokątną można obrzeżyć trójkątami lub „trójkątami” z jednym bokiem krzywoliniowym; stosuje się przy tym sposoby opisane w § 7.7.3.

7.7.3. Nieregularne siatki trójkąta

Siatka złożona z dowolnych trójkątów jest wygodnym środkiem aproksymacji złożonego obszaru płaskiego. Jest zupełmc łatwo zaprogramować automatyczne zagęszczanie rzadkiej siatki trójkątnej; zob. rys. 7.7.6. Łatwo też dostosowywać gęstość siatki do zachowania się funkcji.

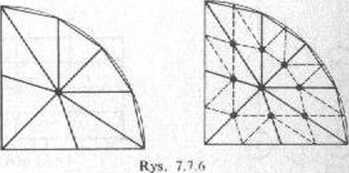
Siatki trójkątne są więc bardziej giętkie w użyciu niż prostokątne. Z drugiej strony, posługiwanie się siatką prostokątną mniej obciąża pamięć i daje prostsze programy, a cza sem także nieco prostsze wzory, w porównaniu z siatką trójkątną. W ostatnich łatach siatki trójkątne zyskały ważne zastosowanie w metodzie elementu skończonego dla zagadnień mechaniki ośrodków ciągłych i innych zadań związanych z równaniami różniczkowymi cząstkowymi; zob. § 8.6.5. Niech punkty = yd (i—1, 2, 3) będą wierzchołkami trójkąta T (rys. 7.7.7). Wtedy każdy punki P=(x, y) na płaszczyźnie można jednoznacznie wyrazić w postaci wektorowej

(7.7.13)    P = 0iP_x + 0₂P₂ +0_}P₃. gdzie 0,+0₂+0₃~l

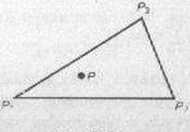
Rys. 7.7.7