DSC00869 (2)

Estymacja punktowa i przedziałowa 137

Sprawdzenie, czy wynik obliczeń odchylenia standardowego (przykład 4.3) jest równy pierwiastkowi nieobciążonego estymatora wariancji (przykład 4.2), pozostawiamy Czytelnikowi.

4.2. Estymacja przedziałowa

4.2.1. Przedział ufności dla wartości oczekiwanej

Konstrukcja przedziału ufności dla wartości oczekiwanej na podstawie małej próby wymaga poczynienia założenia o normalności rozkładu badanej cechy w populacji generalnej. Wykorzystując wyniki próby o liczebności n, obliczamy końce przedziału ufności wg wzoru:

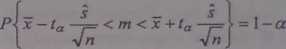
(4.25)

gdzie: x jest średnią arytmetyczną wyników próby, i estymatorem punktowym odchylenia standardowego obliczonym zgodnie ze wzorem (4.24), t_a wartością zmiennej t Studenta wyznaczoną z tablic tego rozkładu, przy liczbie stopni swobody równej n — 1. Wartość ta ustalana jest w ten sposób, że dla danego z góry prawdopodobieństwa 1 — cc, zwanego poziomem itfhości, zachodzi podwójna relacja P{-t_a <t< +/„}=! - a (rys. 4.4).

l-<x

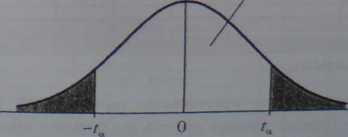
t

Rys. 4.4. Rozkład t Studenta