DSC00875 (6)

Estymacja punktowa i przedziałowa 143

d = t

m

(4.27)

zaś przedziału (4.26):

rn

(4.28)

Jak widać, im większy jest rozrzut wyników pomiarów, tym szerszy będzie przedział ufności. Miarą rozrzutu jest tutaj estymator odchylenia standardowego i. Szerokość wyraźnie zależy od liczebności próby losowej n: im więcej pomiarów zawiera próba, tym węższy jest przedział ufności. Ostatnim czynnikiem wpływającym na szerokość jest wartość t_a we wzorze (4.27) lub u_a we wzorze (4.28). Szerokość przedziału jest proporcjonalna do tej wartości, a ta z kolei zależy przede wszystkim od przyjętego poziomu ufności 1 —a. Im wyższy jest ten poziom, tym wyższe są zarówno jak i a więc przy poziomie ufności bardzo bliskim jedności uzyskuje się bardzo szerokie przedziały ufności. Dlatego przyjmowanie np. wartości 1—a=0,999 powinno mieć wyraźne uzasadnienie.

Wartość t_a zależy ponadto od liczebności próby n, a dokładniej — od liczby stopni swobody n— 1, przy czym im mniejsza jest ta liczba, tym większa jest wartość ta, zatem szerszy będzie przedział ufności.

4.2.2. Przedział ufności dla odchylenia standardowego

W zależności od liczebności próby losowej rozróżnia się dwie postacie przedziału ufności dla odchylenia standardowego. Gdy próba jest mała, wyznacza się w zasadzie przedział ufności dla wariancji, a następnie pierwiastkując jego końce uzyskuje się przedział ufności dla odchylenia standardowego. Gdy natomiast dysponujemy próbą o dużej liczebności, to możemy zbudować bezpośrednio przedział ufności dla odchylenia standardowego. Rozważmy obydwa przypadki.

Jeżeli z populacji generalnej, charakteryzującej się rozkładem normalnym badanej cechy, wylosowano małą próbę o liczebności n, to przedział ufności dla wariancji buduje się zgodnie ze wzorem:

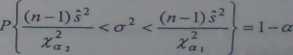
(4.29)