DSC00872 (2)

140 Estymacja punktowa I przedziałowa

eii    rj, Tgj =SA$ 12+t At 16't At I3/PIERVVIASTEI<(t At i ,n

: 'im—rrTffl^r '    ¹ *""l lilii" l' l n ■    i ii -ii - iri" -i 11 -----r 11 ■ i ~ ■    i i

	B83? , B ; • „■		HHSB
md 64.2	Średnia
TO 0.40	Odch. stand.
flŚH 9	n
H 1,95	f-Ot
H 2.306
KUŚ Przedział ufności
ftffij 63.9| 64.6

Rys. 4.5d. Rozwiązanie przykładu 4.4

Odpowiedź: Przedział ufności o końcach 63,9 oraz 64,6 HRC pokrywa rzeczywistą średnią twardość stali SW7M po hartowaniu z zakresu temperatur 1170*1230°C z prawdopodobieństwem 0,95.

Jeżeli nie można poczynić założenia o normalności rozkładu badanej cechy w populacji generalnej, należy zadbać o to, by liczebność próby była możliwie jak największa (co najmniej kilkadziesiąt). Przypomnijmy, że umownie próbę o liczebności n<30 uznaje się za próbę małą, zaś po przekroczeniu tej liczby uważa się, iż próba jest duża.

Przedział ufności dla wartości oczekiwanej przy wykorzystaniu wyników dużej próby budujemy stosując wzór:

p\x-u_a-^=<m<x+u_a—=Ą = \-a    (4.26)

| dn    V« J

gdzie H jest wartością zmiennej losowej U mającej rozkład normalny standaryzowany. Wartość ta odczytywana jest z tablicy dystrybuanty rozkładu normalnego N(0,1), tak aby spełniona była relacja P{-u_a <U< +w_a}=l - a (rys. 4.6).

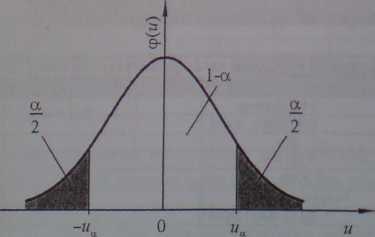
Rys. 4.6. Rozkład normalny standaryzowany N(0,1)