DSC00877 (7)

152 Estymacja punktowa i przedziałowa

dowany przy przyjęciu poziomu ufności 1-a. W tym ujęciu wzór (4.34) można zapisać w bardziej użytecznej formie:

n

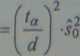
(4.35)

Oczywiście, tylko wyjątkowy zbieg okoliczności może spowodować, że wynikiem obliczeń z zastosowaniem wzoru (4.35) będzie liczba naturalna; liczba pomiarów zawsze jest liczbą naturalną. Stąd po obliczeniu wartości n należy ją zaokrąglić do najbliższej liczby naturalnej zawsze w górę.

Jeżeli ustalona w powyższy sposób docelowa liczba pomiarów n nie przekroczy liczebności wstępnej, czyli gdy zajdzie relacja |||| to wstępnie wykonane pomiary zapewniają już osiągnięcie zamierzonego celu. Szerokość przedziału ufności dla wartości średniej na pewno nie przekroczy w tym przypadku wartości 2d. Jeżeli natomiast zajdzie relacja «>% konieczne będzie wykonanie dodatkowej serii pomiarów o liczebności n-n_Q.

Przykład 4.9

Zakładając, że pierwszych 5 pomiarów z przykładu 4.4 stanowi próbę wstępną, obliczyć docelową liczbę pomiarów, jakie należy wykonać, aby zbudować przedział ufności dla średniej twardości stali SW7M po zabiegu hartowania o szerokości nie przekraczającej 1,1 HRC, przy poziomie ufności 1 - o=0,95.

Rozwiązanie

Do komórek A2:A6 wprowadzono pomiary uzyskane w próbie wstępnej, w komórce A8 oszacowano wstępnie wariancję śo, | liczbę pomiarów próby wstępnej ustalono w komórce A9. Wartość połowy szerokości docelowego przedziału ufności d wprowadzono do komórki A10.

Biorąc pod uwagę sposób wyznaczania wartości ffj do komórki A9 wprowadzono zamiast poziomu ufności 1-a wartość a, co ułatwiło odczyt wartości tablicowej (komórka A12). W komórce A13 obliczono za pomocą formuły widocznej w pasku formuły docelową liczbę pomiarów niezbędnych do wykonania, aby na