Opracowanie: Łukasz Urbańczyk
WYKŁAD 25
CAŁKI KRZYWOLINIOWE
PRZYKŁAD 25.1
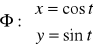
Taka parametryzacja okręgu zadaje nam kierunek przeciwny do ruchu wskazówek zegara
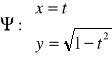
Ta parametryzacja zadaje nam kierunek zgodny z ruchem wskazówek zegara
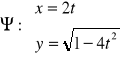
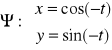
Zgodnie z ruchem wskazówek zegara
Parametryzacje tej samej krzywej mogą różnić się orientacją
Klasa
- kierunek przeciwny do ruchu wskazówek zegara
Klasa
- kierunek zgodny z ruchem wskazówek zegara
DEFINICJA 25.1 (PARAMETRYZACJA REGULARNA)
- parametryzacja regularna 
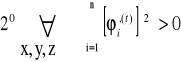
DEFINICJA 25.1 (PARAMETRYZACJE RÓWNOWAŻNE)
Niech 
- parametryzacja regularna
- parametryzacja regularna
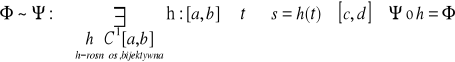
UWAGA:
Jeżeli 
to 
, zbiór wartości 
pokrywają się ,
ponadto jest zachowany kierunek na krzywej (mają taką samą orientację)
TWIERDZENIE 25.1 (RÓWNOWAŻNOŚĆ PARAMETRYZACJI)
Równoważność parametryzacji jest relacją równoważnościową.
Oznaczenie „~” - relacja równoważnościowa
Dowód:
-zwrotność : 
-symetria 
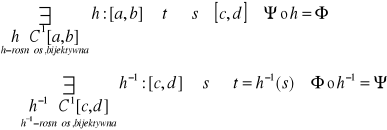
-przechodniość 
Niech : 
- parametryzacja regularna
Z: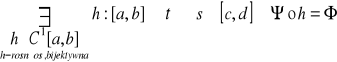 
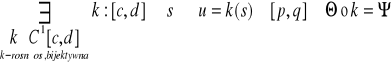
T: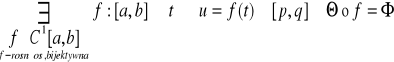 
, gdzie 
Złożenie bijekcji jest bijekcją
Złożenie funkcji rosnących jest funkcją rosnącą
UWAGA:
Parametryzacje należące do tej samej klasy równoważności mają ten sam zbiór wartości i wyznaczają ten sam kierunek
DEFINICJA 25.3 (ŁUK REGULARNY)
Niech 
- parametryzacja regularna
K=[
] - łuk regularny
A=
(a) - początek łuku K , B=
(b) - koniec łuku K
DEFINICJA 25.4
Niech 
,
- parametryzacje regularne
K=[
] , K'=[ 
]
K'- ma orientacje przeciwną do K
OZNACZENIE
K'= -K - łuk o orientacji przeciwnej do łuku K
Uwaga.
Początek (-K)=koniec K , koniec(-K) = początek K
DEFINICJA 25.5
F - ciągła (różniczkowalna) na łuku K=[
] : 
- ciągła (różniczkowalna)
na [a,b]
DEFINICJA 25.6 (CAŁKA KRZYWOLINIOWA ZORIENTOWANA)
Niech K=[
] - łuk regularny
- określone i ciągłe na K
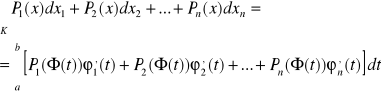
TWIERDZENIE 25.2 (O NIEZALEŻNOŚCI CAŁKI OD PARAMETRYZACJI)
Całka krzywoliniowa zorientowana nie zależy od wyboru parametryzacji łuku
Dowód:
Niech K=
Z założenia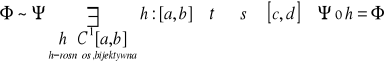 
Z definicji całki dla Φ⇒
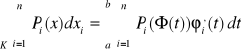
dla Ψ
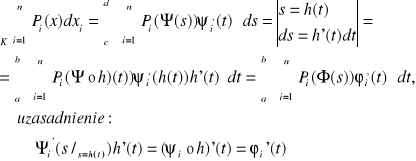
TWIERDZENIE 25.3
Zmiana orientacji łuku powoduje jedynie zmianę znaku całki
Dowód:
Niech K=[
] , -K=[ 
]
Gdzie 
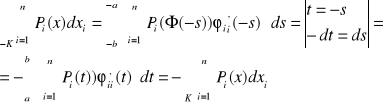
DEFINICJA 25.7 (KRZYWA REGULARNA)
L- krzywa regularna 
(mające co najwyżej wspólne końce )
L=(K1, K2,...,Km) 
koniec łuku Ki = początek łuku Ki+1
Jeżeli ponadto koniec Km = początek K1 to L -krzywa regularna zamknięta
DEFINICJA 25.8 (KRZYWA REGULARNA)
L- krzywa regularna to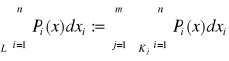 
PRZYKŁAD 25.2
-łuk paraboli 
,
A(2,4) B(1,1)
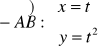
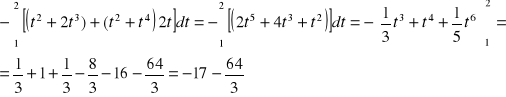
1