Opracowanie: Marek Stolarski

WYKŁAD 11

OBLICZANIE GRANIC FUNKCJI DWÓCH ZMIENNYCH

Niech będzie dana funkcja:

Będziemy badać granicę:

Do punktu na płaszczyźnie można zmierzać po dowolnej krzywej kończącej się w punkcie (x₀, y₀).

y

(x₀, y₀)

x

Jeżeli wprowadzimy współrzędne biegunowe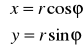

to zauważymy, że: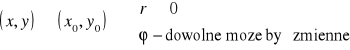

UWAGA:

1. Jeżeli dla każdej drogi istnieje granica i jest zawsze taka sama (=g), to wtedy funkcja posiada granicę.

2. Jeżeli dla dwóch różnych dróg wartości granic są różne, to funkcja granicy nie posiada.

PRZYKŁAD 11.1

Obliczmy granice:

1°

Jeżeli mamy iloraz dwóch wielomianów warto spróbować wprowadzić współrzędne biegunowe.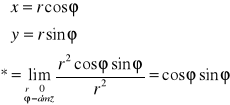


Ta granica nie istnieje, bo jej wartość zależy od φ, a więc od drogi.

2°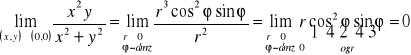

3°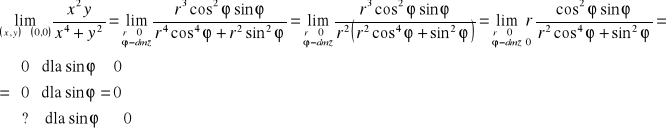

Dobierzmy krzywą, tak aby
, a w mianowniku zredukowała się suma x⁴+y²
Niech y=x², wtedy granica 3° wyniesie:


Ta granica nie istnieje ponieważ znaleźliśmy drogę (Por. Uwaga 2), dla której wartość granicy jest różna od wartości granicy dla innych dróg.

4°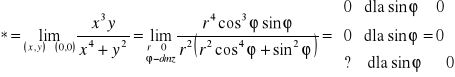


Zmierzamy po krzywej y=x²

- to nie jest kontrprzykład, więc granica 4° może istnieć.
Spróbujemy oszacować naszą funkcję: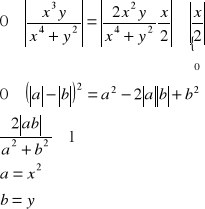


Na podstawie twierdzenia o trzech funkcjach wartość granicy 4° jest równa 0.

UWAGA:

Wszystkie sposoby, które stosowaliśmy do funkcji jednej zmiennej (za wyjątkiem reguły de l'Hospitala) stosujemy do funkcji dwóch zmiennych.

GRANICE ITEROWANE

lub

UWAGA:

Może się zdarzyć, że:

1. Istnieje
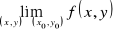
   i nie istnieją granice iterowane.

2. Istnieją granice iterowane i nie istnieje
   .

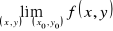
Jeżeli istnieją granice iterowane i są one różne to możemy wyciągnąć wniosek, że granica nie istnieje.

PRZYKŁAD 11.2

1°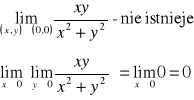

2°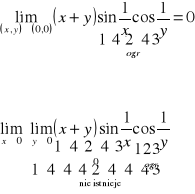

Niech będą dane X, Y - przestrzenie Banacha nad

DEFINICJA 11.1 (OBSZAR)

Powiemy, że

Niech
- odwzorowanie

DEFINICJA 11.2 (POCHODNA KIERUNKOWA)

Niech
takim, że

Pochodna w kierunku wektora h:

Pochodną kierunkową nazywamy pochodną w kierunku wersora wektora h,

PRZYKŁAD 11.3

Niech

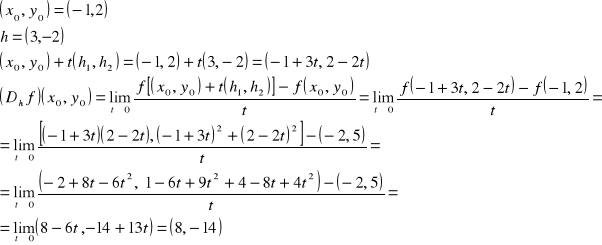
Niech

DEFINICJA 11.3 (POCHODNE CZĄSTKOWE)

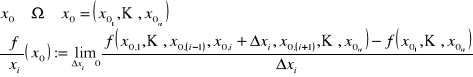
WNIOSEK 11.1

, gdzie
- to
-ty wektor bazy kanonicznej
.

UWAGA:

W
mamy bazę kanoniczną


pełni rolę t

DEFINICJA 11.4 (RÓŻNICZKOWALNOŚĆ I RÓŻNICZKA)

Niech:

Rozważmy przyrost funkcji odpowiadający wektorowi przyrostu h.
x₀ - ustalone h- zmienne


Jeżeli
, to powiemy, że f jest różniczkowalna w punkcie x₀ oraz

- nazwiemy różniczką funkcji w punkcie x₀ i oznaczamy ją df (x₀)

UWAGA:




- przestrzeń odwzorowań liniowych i ciągłych
Różniczka w punkcie jest to odwzorowanie liniowe i ciągłe.

PRZYKŁAD 11.4

Zbadać różniczkowalność funkcji i określić różniczkę

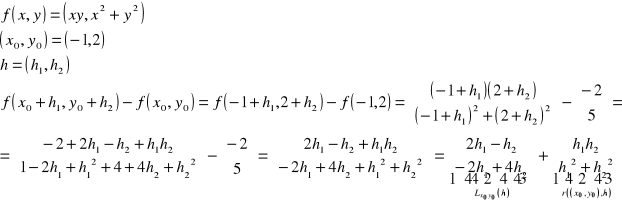
Badamy granicę: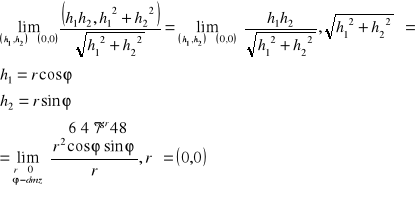


Funkcja jest różniczkowalna w punkcie (x₀,y₀)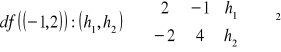

TWIERDZENIE 11.1 (O JEDNOZNACZNOŚCI RÓŻNICZKI W PUNKCIE)

Z: X,Y - przestrzenie Banacha

- odwzorowanie,
- obszar


f jest różniczkowalna w punkcie x₀,

- różniczki funkcji f w punkcie x₀

T:

D:

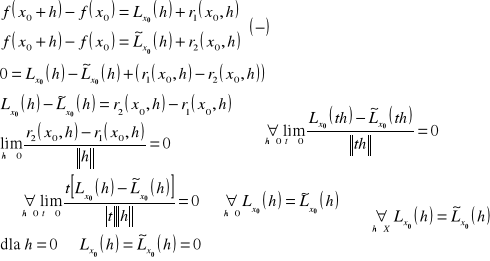
UWAGA:

Jeżeli

to
nazwiemy różniczką funkcji f.

TWIERDZENIE 11.2 (WŁASNOŚCI RÓŻNICZKI)

Z:

f, g - różniczkowalne w punkcie x₀

T:
1°
- różniczkowalna w punkcie x₀
2°


D:

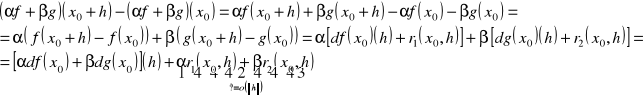
Badamy: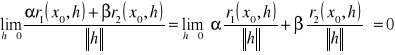

TWIERDZENIE 11.3 (ZWIĄZEK RÓŻNICZKI Z POCHODNYMI W

KIERUNKU WEKTORA)

Z:

- odwzorowanie X,Y - przestrzenie Banacha

, f - różniczkowalna w punkcie x₀

T:

D: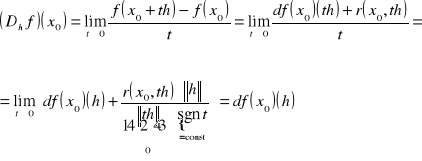

WNIOSEK 11.2 (ZWIĄZEK RÓŻNICZKI Z POCHODNYMI CZĄSTKOWYMI)

Niech
Y - przestrzeń Banacha


f - różniczkowalna w punkcie x₀

T:

1°

2°

f różniczkowalna

ma pochodne w kierunku

f ciągła ? dowolnego wektora

ma wszystkie pochodne cząstkowe

i zachodzi wzór:

TWIERDZENIE 11.4

Jeżeli



istnieją i są ciągłe
to f jest różniczkowalna w punkcie x₀ i zachodzi wzór: