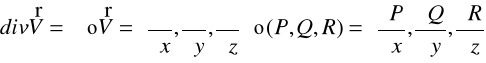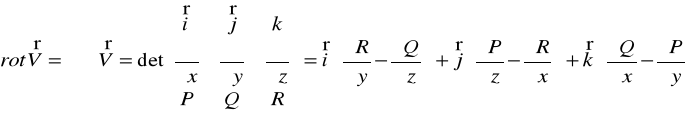Opracowanie: Artur Siara

WYKŁAD 28

TWIERDZENIE 28.1 (OSTOGRADSKIEGO - GAUSSA)

Z:
- obszar normalny względem płaszczyzn układu współrzędnych

- powierzchnia regularna zamknięta zorientowana na zewnątrz V

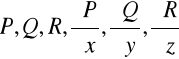
są określone i ciągłe na

T: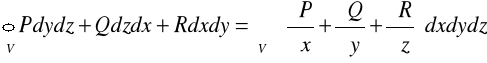

DEFINICJA 28.1 (ZGODNOŚĆORIENTACJI PŁATA I JEGO BRZEGU)

Powiemy, że płat S i jego brzeg ∂S mają orientację zgodną z orientacją układu współrzędnych, jeżeli:

1. układ Oxyz jest prawoskrętny, to układ kierunek brzegu i wektor normalny jest też prawoskrętny,

2. układ Oxyz jest lewoskrętny, to układ kierunek na krzywej i wektor normalny do powierzchni jest też lewoskrętny.

TWIERDZENIE 28.2 (STOKESA)

Z: S - płat regularny

∂S - krzywa regularna zamknięta

P, Q, R - są określone i różniczkowalne w S ∪ ∂ S

T: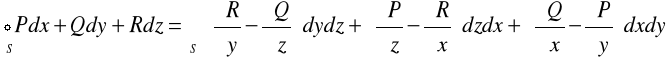

D:

1. 
   

2. 
   

3. 
   

Tak więc:

(funkcja spełnia założenia twierdzenia Greena)

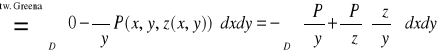
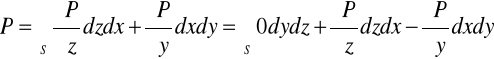
Ale: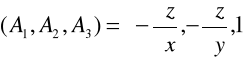

Wobec tego:

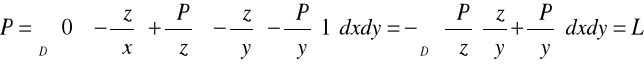
Pozostałe dwie zależności dowodzi się analogicznie.

TEORIA POLA

DEFINICJA 28.2 (POLE WEKTOROWE)

Czyli w
:

w
:

DEFINICJA 28.3 (POLE POTENCJALNE)

- nazwiemy potencjalnym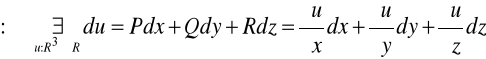

Przy czym funkcje
nazywamy potencjałem pola wektorowego
.

DEFINICJA 28.4 (ROTACJA POLA WEKTOROWEGO)

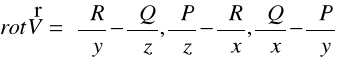
STWIERDZENIE 28.1

Pole wektorowe
jest potencjalne

WNIOSEK 28.1 (Z TW. STOKESA)

Jeżeli
w obszarze
, to całka krzywoliniowa w tym obszarze nie zależy od drogi - zależy jedynie od początku i końca krzywej - a ponadto:

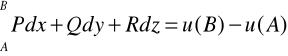
WNIOSEK 28.2

Jeżeli
i są spełnione założenia tw. Stokesa, to
jest potencjalne
i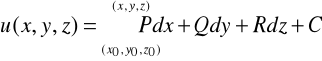

PRZYKŁAD 28.1

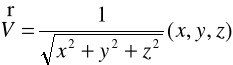
1. sprawdzić, czy
   jest potencjalne

2. obliczyć potencjał

obliczyć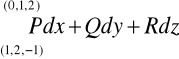

ad a)

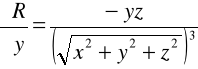
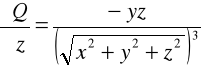
Analogicznie sprawdzamy dla pozostałych współrzędnych,

czyli, że: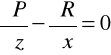

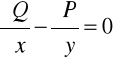
ad b)

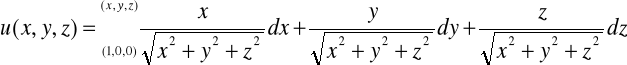
Zał: x>0, y>0, z>0

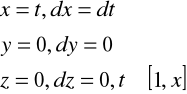
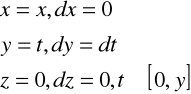
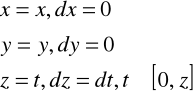
Wobec tego:

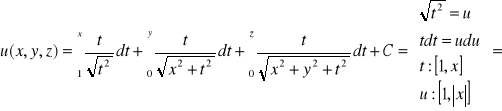
Czyli:

ad c)

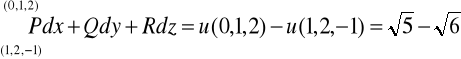
DEFINICJA 28.5 (DIVERGENCJA)

Jeżeli

to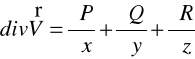

DEFINICJA 28.6 (GRADIENT)

Mamy daną funkcję

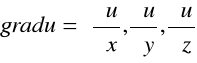
WNIOSEK 28.3

Jeżeli
- potencjalne,
- potencjał pola

to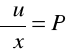

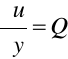
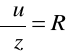
Gradient potencjału jest tym samym polem.

Operator ∇ (nabla)

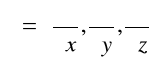
WNIOSKI

1. 
   

2. 
   

v

x

y

z

z

y

x

S

u

∂S

→

mają orientację zgodną z Oxyz

→

∂S

u

S

z

y

x

z = z(x,y)

D

∂D

*

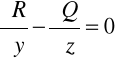
L₁:

L₃:

L₂:

L₂

L₁

(1,0,0)

(x,0,0)

z

y

x

(x,y,0)

(x,y,z)

L₃

---