Opracowanie: Tomasz Wąsala

WYKŁAD 27

DEFINICJA 27.1 (PARAMETRYZACJA REGULARNA)

Niech:

- obszar (zbiór otwarty i spójny)

ℑ :
∋

ℑ -parametryzacja regularna :⇔

1°

2° ℑ - ciągła i różniczkowalna w

3° ℑ - różnowartościowa (iniekcja)

4° W Każdym punkcie powierzchni R_ℑ istnieje

wektor (A₁,A₂,A₃) ⊥ R_ℑ,

przy czym:

(A₁,A₂,A₃) =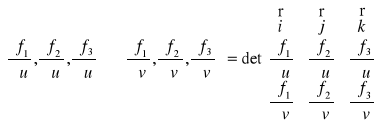

Wyjaśnienie:

R_ℑ - zbiór wartości odwzorowania ℑ (powierzchnia)

PRZYKŁAD 27.1

I.

z=z(x,y),

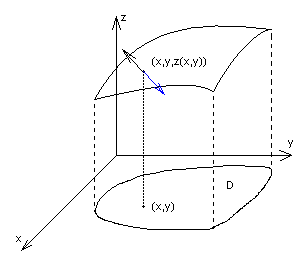
Niech:

ℑ :
∋
- parametryzacja naturalna

(A₁,A₂,A₃) =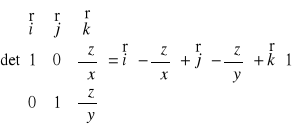

,czyli:

(A₁,A₂,A₃) =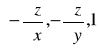

II.

Gdy powierzchnia jest wykresem funkcji zmiennych x, z:

y=y(x,z),

ℑ :
∋

Po analogicznym wyprowadzeniu jak w przypadku pierwszym:

(A₁,A₂,A₃) =

III.

Gdy powierzchnia jest wykresem funkcji zmiennych y, z:

x=x(y,z),
₁

ℑ :
∋

Więc:

(A₁,A₂,A₃) =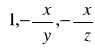

TWIERDZENIE 27.1

Z: ℑ :
∋
- parametryzacja

regularna

Niech:

κ : Δ ∋

κ - bijekcja, różniczkowalna

Niech:

G = ℑ
κ : Δ ∋
G

=

Niech:

(B₁,B₂,B₃) - wektor prostopadły do R_G

T: 1° R_ℑ = R_G

2° (B₁,B₂,B₃) = (A₁,A₂,A₃)∙Jκ

,gdzie:

Jκ =
- jakobian odwzorowania κ

D: Ad 1° ⇐ z założeń (bezpośrednio)

Ad 2°

(B₁,B₂,B₃)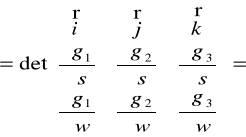

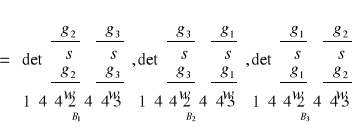
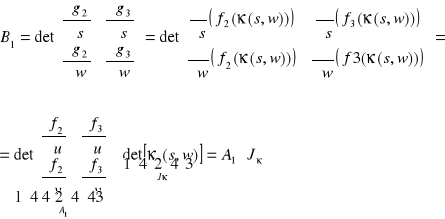
Dowód dla B₂, B₃ przeprowadza się analogicznie jak dla B₁.

DEFINICJA 27.2 (PARAMETRYZACJE RÓWNOWAŻNE)

ℑ ∼ G ⇔
G=
Jκ

UWAGA:

1° R_ℑ = R_G

2° (A₁,A₂,A₃) oraz (B₁,B₂,B₃) mają ten sam kierunek, ten sam zwrot.

TWIERDZENIE 27.1

Relacja „∼” - jest relacją równowartościową.

DEFINICJA 27.3 (PŁAT POWIERZCHNIOWY REGULARNY)

S = [ℑ] -płat powierzchniowy regularny.

DEFINICJA 27.4 (ORIENTACJA PŁATA)

Niech:

S = [ℑ]

(-S) = [G]

(-S) jest zorientowany przeciwnie do S :⇔ G
∋
G

Zauważmy, że:

Jeżeli κ ∋

Jκ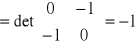

Wniosek:

(B₁,B₂,B₃) = - (A₁,A₂,A₃)

DEFINICJA 27.5

Niech

-określona, ciągła, różniczkowalna (…) na płacie powierzchniowym S=[ℑ]⇔

⇔
-określona ciągła różniczkowalna (…) w
.

DEFINICJA 27.6 (CAŁKA POWIERZCHNIOWA NIESKIEROWANA)

Niech
-określona i ciągła na S=[ℑ]

PRZYKŁAD 27.2

Jeżeli

S: z=z(x,y),

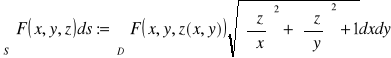
WNIOSEK 27.1

1° Całka powierzchniowa niekierowana nie zależy od wyboru parametryzacji płata.

2° Całka powierzchniowa niekierowana nie zależy od orientacji płata.

DEFINICJA 27.7 (POWIERZCHNIA REGULARNA)

S - powierzchnia regularna ⇔ S
-są płatami powierzchniowymi, przy czym sąsiednie S_i mają wspólne krawędzie.

DEFINICJA 27.8

Jeżeli S - powierzchnia regularna

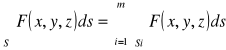
CAŁKA POWIERZCHNIOWA ZORIENTOWANA

Niech:

S = [ℑ] - płat powierzchniowy,

(A₁,A₂,A₃) wektor ⊥ S,

,

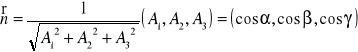
,gdzie α,β,γ są to kąty jakie tworzy wektor
z osiami układu.

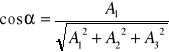
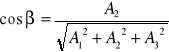
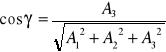
DEFINICJA 27.9 (CAŁKA POWIERZCHNIOWA ZORIENTOWANA)

Niech:

- określone i ciągłe na S

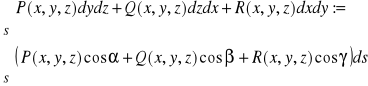
Uwaga:

WNIOSEK 27.2

1° Całka powierzchniowa zorientowana nie zależy od wyboru parametryzacji płata.

2° Całka powierzchniowa zorientowana zależy od orientacji płata

PRZYKŁAD 27.3

S: z = z(x,y),

(A₁,A₂,A₃) =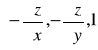

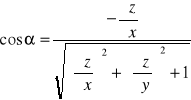
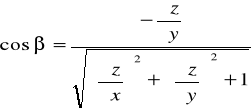
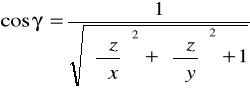
Jeżeli
- określone i ciągłe na S, to:

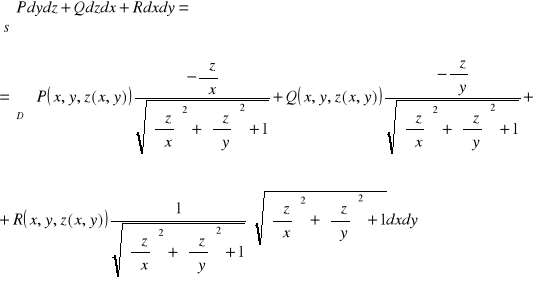
S: z = z(x,y),

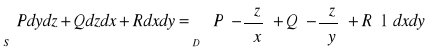
Umowa:

S: z = z(x,y),

S - zorientowana dodatnio względem osi Oz ⇔ cosγ >0

np.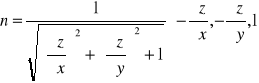

S: y= y(x,z),

S - zorientowana dodatnio względem osi Oy ⇔ cosβ >0

S: x= x(y,z),

S - zorientowana dodatnio względem osi Ox ⇔ cosα >0