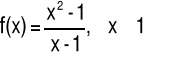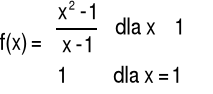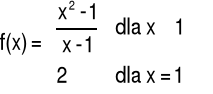3.6 Funkcje ciągłe
Ciągłość funkcji
Definicja (funkcja ciągła w punkcie)
Niech x0∈R oraz niech funkcja f będzie określona przynajmniej na otoczeniu O(x0). Funkcja f jest ciągła w punkcie x0 wtedy i tylko wtedy, gdy
|
(3.6.1) |
Uwaga: warunek (3.6.1) można rozpisać w sposób następujący:
|
(3.6.2) |
|
(3.6.3) |
|
(3.6.4) |
Interpretacja geometryczna
|
|
|
|
|
|
nieciągłość w 1 |
nieciągłość w 1 |
ciągłość w 1 |
Definicje (funkcja ciągła w przedziale)
Funkcja ciągła w każdym punkcie pewnego przedziału (otwartego lub domkniętego) nazywa się funkcją ciągłą w tym przedziale.
3.6 Funkcje ciągłe
Ciągłość jednostronna funkcji
Definicja (funkcja lewostronnie ciągła w punkcie)
Niech x0∈R oraz niech funkcja f będzie określona przynajmniej na otoczeniu ![]()
. Funkcja f jest lewostronnie ciągła w punkcie x0 wtedy i tylko wtedy, gdy
|
(3.6.5) |
Definicja (funkcja prawostronnie ciągła w punkcie)
Niech x0∈R oraz niech funkcja f będzie określona przynajmniej na otoczeniu ![]()
. Funkcja f jest prawostronnie ciągła w punkcie x0 wtedy i tylko wtedy, gdy
|
(3.6.6) |
Twierdzenie
(Warunek konieczny i wystarczający ciągłości funkcji)
Funkcja jest ciągła w punkcie wtedy i tylko wtedy, gdy jest w tym punkcie ciągła lewostronnie i prawostronnie.
Definicje (funkcja ciągła na przedziale)
Funkcja f jest ciągła w przedziale |
jeżeli jest ciągła |
(a,b) , |
w każdym punkcie tego przedziału |
[a,b) , |
w (a,b) i prawostronnie ciągła w a |
(a,b] , |
w (a,b) i lewostronnie ciągła w b |
[a,b] , |
w (a,b), prawostronnie ciągła w a i lewostronnie ciągła w b |
(-∞,b] , |
w (-∞,b) i lewostronnie ciągła w b |
[a,+∞) , |
w (a,+∞) i prawostronnie ciągła w a |
3.6 Funkcje ciągłe
Działania na funkcjach ciągłych
Twierdzenie
(O ciągłości sumy, różnicy, iloczynu i ilorazu funkcji)
Jeżeli funkcje f i g są ciągłe w punkcie x0, to:
1) funkcja f + g jest ciągła w punkcie x0,
2) funkcja f - g jest ciągła w punkcie x0,
3) funkcja f⋅g jest ciągła w punkcie x0,
4) funkcja ![]()
jest ciągła w punkcie x0 o ile g(x0) ≠ 0.
Uwaga: Twierdzenie jest prawdziwe dla także dla funkcji ciągłych jednostronnie.
Twierdzenie (O ciągłości funkcji złożonej)
Jeżeli:
1) funkcja f jest ciągła w punkcie x0,
2) funkcja g jest ciągła w punkcie y0 = f(x0),
to funkcja złożona g(f) jest ciągła w punkcie x0.
Twierdzenie (O ciągłości funkcji odwrotnej)
Niech A oraz B będą dowolnymi przedziałami. Jeżeli funkcja f: A→B jest ściśle monotoniczna i ciągła, to funkcja odwrotna f-1: B→A jest także ciągła.
Twierdzenie (O ciągłości funkcji elementarnej)
Funkcje elementarne są ciągłe w swoich dziedzinach.
Twierdzenie
(O monotoniczności funkcji ciągłej i różnowartościowej)
Niech funkcja f będzie ciągła na przedziale A. Wówczas funkcja f jest różnowartościowa na tym przedziale wtedy i tylko wtedy, gdy jest tam ściśle monotoniczna.
3.6 Funkcje ciągłe
Przykład 1 Zbadać ciągłość funkcji f w punkcie x=0
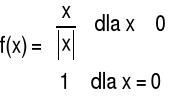
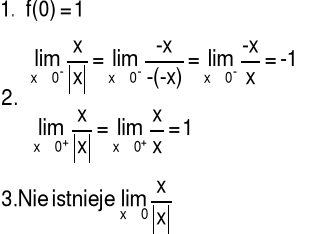
Odpowiedź: Funkcja f nie jest ciągła w punkcie x=0.
Przykład 2 Zbadać ciągłość funkcji f w punkcie x=0
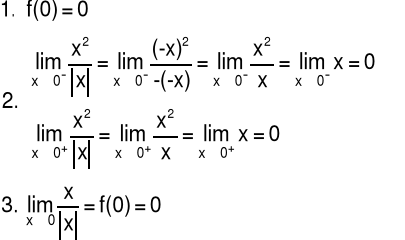
Odpowiedź: Funkcja f jest ciągła w punkcie x=0.
3.6 Funkcje ciągłe
Przykład 3 Zbadać ciągłość funkcji f w punkcie x=0
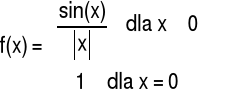
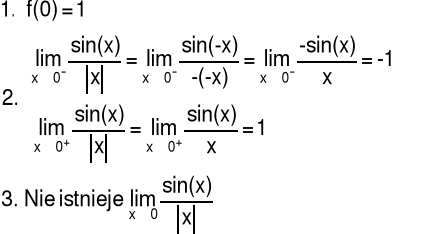
Odpowiedź: Funkcja f nie jest ciągła w punkcie x=0.
Przykład 4 Zbadać ciągłość funkcji f w punkcie x=0
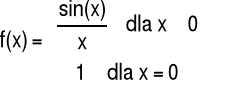
Odpowiedź: Funkcja f jest ciągła w punkcie x=0.
3.6 Funkcje ciągłe
Przykład 5 Uzasadnić ciągłość funkcji:
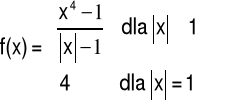
Rozwiązanie:
• Zauważmy najpierw, że dla |x|≠1 mamy:
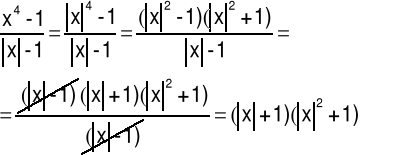
• Wykazanie, że funkcja f jest ciągła w każdym punkcie x0 spełniającym warunek |x0| ≠ 1.
Zatem:
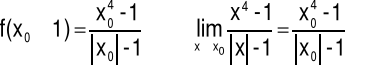
Oznacza to, że funkcja f jest ciągła w każdym punkcie x0.
• Niech x0 będzie liczbą spełniającą warunek |x0|=1. Wtedy:
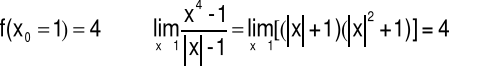
Oznacza to, że funkcja f jest ciągła w punkcie x0=1.
Odpowiedź:
Badana funkcja f jest ciągła w zbiorze R.
3.7 Nieciągłość funkcji
Definicja (Nieciągłość funkcji)
Niech x0∈R oraz niech funkcja f będzie określona przynajmniej na otoczeniu O(x0). Funkcja f jest nieciągła w punkcie x0 wtedy i tylko wtedy, gdy nie istnieje granica
|
(3.7.1) |
albo, gdy
|
(3.7.2) |
Uwaga: Nieciągłość funkcji można rozważać jedynie w punktach należących do jej dziedziny.
Definicja (Nieciągłość pierwszego rodzaju)
Funkcja f ma w punkcie x0 nieciągłość pierwszego rodzaju, jeżeli istnieją granice skończone
|
(3.7.3) |
oraz
|
(3.7.4) |
Definicje (Nieciągłość pierwszego rodzaju)
Funkcja f ma w punkcie x0 nieciągłość pierwszego rodzaju typu „skok”, jeżeli
|
(3.7.5) |
Funkcja f ma w punkcie x0 nieciągłość pierwszego rodzaju typu „luka”, jeżeli
|
(3.7.6) |
3.7 Nieciągłość funkcji
Przykład 1 Nieciągłość typu „skok”
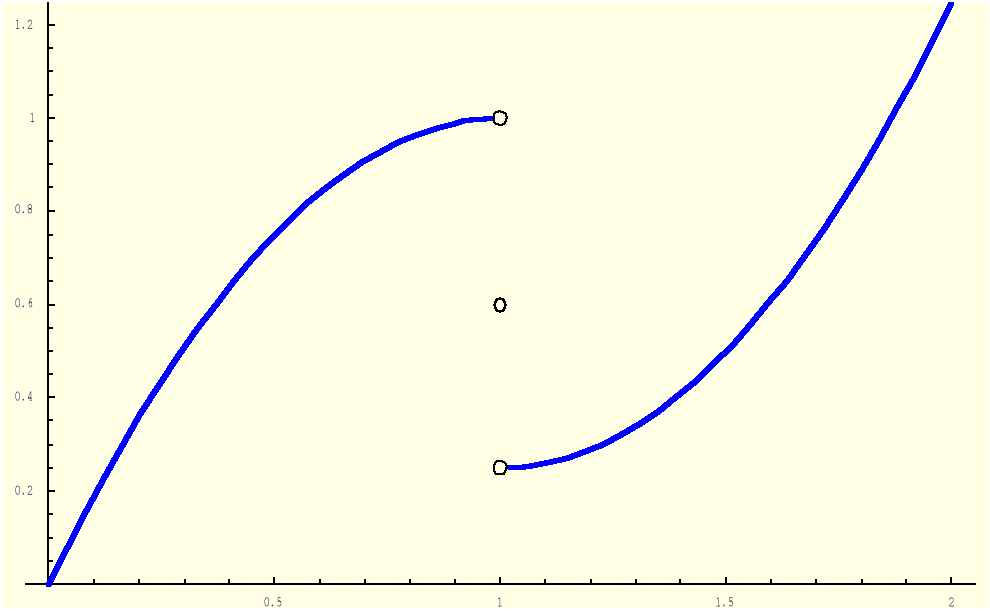
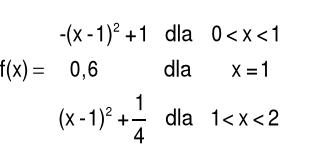
Przykład 2 Nieciągłość typu „luka”
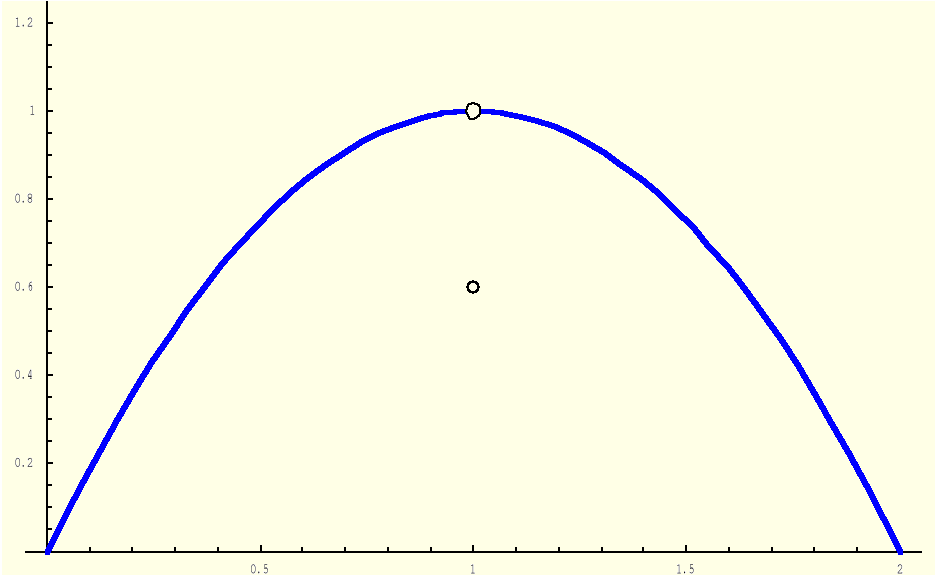
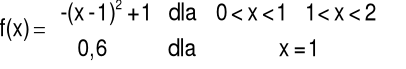
3.7 Nieciągłość funkcji
Definicja (Nieciągłość drugiego rodzaju)
Funkcja f ma w punkcie x0 nieciągłość drugiego rodzaju, jeżeli co najmniej jedna z granic
|
(3.7.7) |
nie istnieje lub jest niewłaściwa.
Przykład 3 Granice jednostronne są niewłaściwe
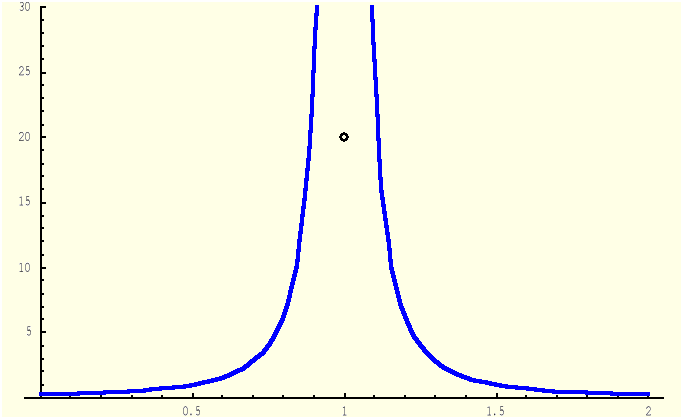
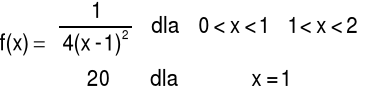
Przykład 4 Granica lewostronna nie istnieje
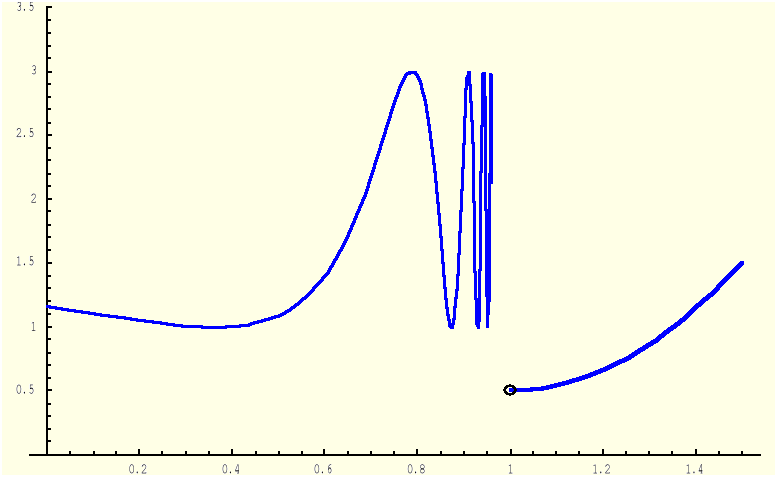
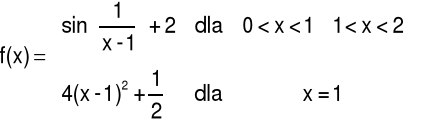
3.7 Nieciągłość funkcji
Przykład 1 Określić rodzaj nieciągłości funkcji f w punkcie x0.
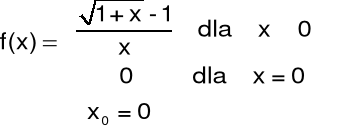
Rozwiązanie:
Funkcja jest nieciągła w punkcie, jeżeli jej granica w tym punkcie nie istnieje albo jest różna od jej wartości.
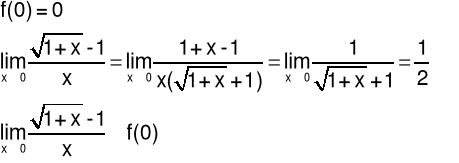
Odpowiedź: Badana funkcja ma w punkcie x0=0 nieciągłość pierwszego rodzaju typu “luka”
Przykład 2 Określić rodzaj nieciągłości funkcji f w punkcie x0.
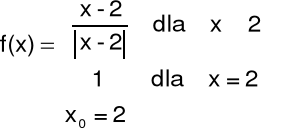
Rozwiązanie:
Funkcja jest nieciągła w punkcie, jeżeli jej granica w tym punkcie nie istnieje albo jest różna od jej wartości.
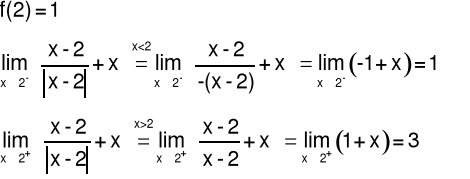
Odpowiedź: Badana funkcja ma w punkcie x0=2 nieciągłość pierwszego rodzaju typu “skok”.
Wyszukiwarka
Podobne podstrony:
5Analiza-7B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-3, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-6D, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-Przykłady-4, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-4B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-2C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-5C, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-7E, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-3A, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
5Analiza-1B, Materiały z Uniwersytetu Szczecińskiego i PS (ZUT)
więcej podobnych podstron