scan 6 (4)

JU

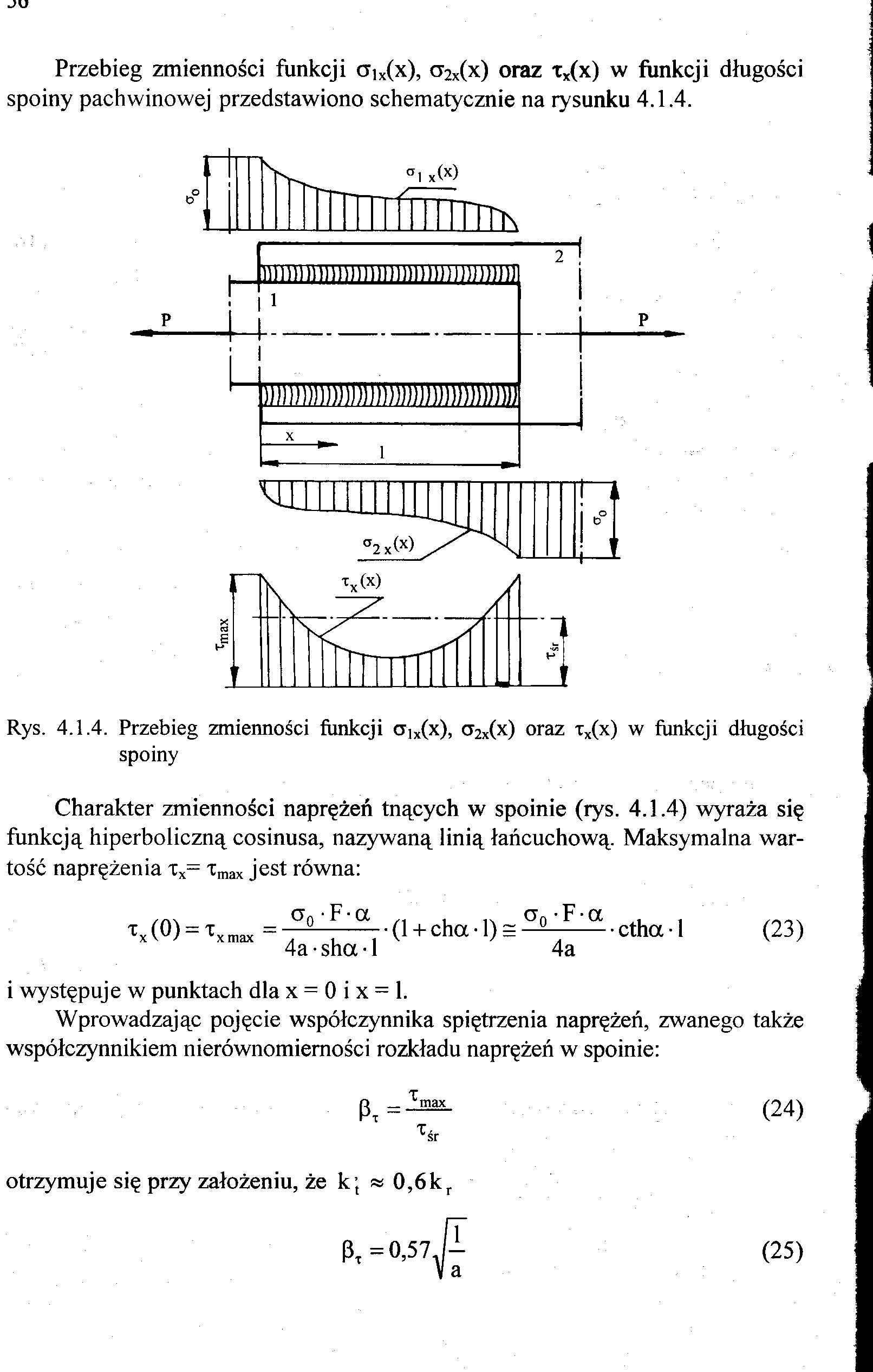
Przebieg zmienności funkcji a_]x(x), a_2x(x) oraz t_x(x) w funkcji długości spoiny pachwinowej przedstawiono schematycznie na rysunku 4.1.4.

JU

_o			^ai „w
0 |				_____Hih

■	K	TX(X) x___^ . A						A
CU 3		^Ns	fnn	n	ti	y			J

Rys. 4.1.4. Przebieg zmienności funkcji CTi_x(x), ct₂x(x) oraz t_x(x) w funkcji długości spoiny

Charakter zmienności naprężeń tnących w spoinie (rys. 4.1.4) wyraża się funkcją hiperboliczną cosinusa, nazywaną linią łańcuchową. Maksymalna wartość naprężenia x_x= T_max jest równa:

i^;x(0) = 't_xmax = 7° U ^a •(l + cha-l)=^CT° ^F -• ctha• 1    (23)

4a • sha • 1    4a

i występuje w punktach dla x = 0 i x = 1.

Wprowadzając pojęcie współczynnika spiętrzenia naprężeń, zwanego także współczynnikiem nierównomiemości rozkładu naprężeń w spoinie:

P_T=^-    (24)

^Xśr

otrzymuje się przy założeniu, że k; « 0,6k_r

(25)

(S,=0,5⁷1|I