Matematyka 2 57

356 V. Elementy rachunku prawJoftodobieńsiwa

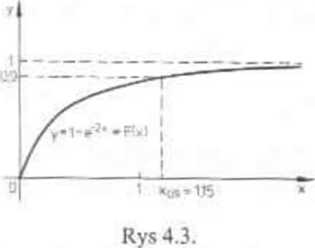
W tym przykładzie udało się nam uzyskać jawny wzór na postać kwanty-ła. Przyjmując teraz p=0,9, X=2 otrzymujemy: x₀₉ =-0,5 ln( 1-0,9) = =0.5 In 10* 1,15, (por. rys 4.3).    ■

WARIANCJA. Omówienie tej podstawowej miary rozproszenia rozpoczniemy od prostego przykładu wprowadzającego nas w zagadnienie.

PRZYKŁAD 4.7 Miech X. Y będąZLS o funkcjach pr-stwn odpowiednio:

\ | -2	2	» 1	-20	15
JH*.)| 0,25	0.75	pty.) I	0.4	0.6

Mają one równe wartości oczekiwane EX- ł£Y= I. Różnią się jednak m/rzutcni swych wartości względem punktu x=l - druga mu bezsprzecznie większy rozrzut Chcemy wprowadzić miarę tego rozrzutu. Miara laka powinna uwzględnić nie tylko "odchylenia" -I oraz y, — 1 ale również pr-stwn. / jukimi się one realizują Jednak bezpośrednio

odchylenia te mc mogą być wykorzystane, ponieważ dla każdej ZL Z zgodnie z ostatnią z własności E2, mamy E(Z HZ) = 0. Pierzemy wobec Jego kwadraty tych odchyleń (Xj-J)². (y, — ł)‘ i obliczamy ich sumy mnożąc uprzednio przez pr-stwa p(x,) i p(yj z. lakimi się one realizują:

( 2 -1)² -0,25 ♦ (2-0* -0.75-3 oraz (-20-1)^: 0.4+<l5-ll^: 0.6=294

Tak określona miara rozrzutu dla ZL Y jest więc. zgodnie 7 pierwszym Intuicyjnym osądem, znacznie większa od miary rozrzutu dla ZL X    B

Realizując myśl zawartą w przykładzie przyjmujemy następujące określenie.

Wariancją ZL X dowolnego lypu, dla której istnieje wartość oczekiwana EX. nazywamy liczbę VarX (oznaczaną również symbolami: D²X, o\ o*. n₂) określoną wzorem

(4.7)    VarX = E(X-EX)-

Jest to więc wartość oczekiwana kwadratu odchyleniu X-EX ZL X <od jej wartości oczekiwanej EX.

Uwzględniając w tej definicji równości (4.3) i (4.4) dla g(X) = = (X - EX)², otrzymujemy:

(4.8)    VarX= ^(x_i-EX)^:p(x_j) dla ZLS X o skokach p(x₄),

«.«w

m

(4.9)    VarX= J(x-EX)²f(x)dx dla ZLC X o GP f.

-a>

Przeanalizujemy wzór (4.8) dla ZLS o skończonej liczbie punktów skokowych:

VarX = (X| -EX)^Jp(X| )+(x₃ - HX)²p(xj)+--'+(x„ - EX)²p(x„).

Wszystkie składniki po prawej strome są meujemne Dlatego wariancja przyjmuje wartość bliską zera (jest mała) wtedy i tylko wiedy. gdy każdy składnik (x, - EX)^:p(x,) jest bliski zera, tj gdy: I) każdy punkt skokowy x, mało różni się od EX lub 2) jeśli punkt skokow'y x, jest znacznie odległy od punktu EX. to pr-stwo p(x,) takiego zdarzenia jest bliskie zera. Zatem: wariancja ZL jest mała jedynie wtedy, gdy zmienna ta przyjmuje wartości x. ze zbioru blisko położonego wartości oczekiwanej HX, a jeśli zdarzają się wartości x, ze zbioru znacznie odległego od punktu EX. to z pr-srwem p(x,) bliskim zera. W tym sensie wariancja ZL jest miarą rozrzutu (rozproszenia) wartości ZL wokół jej wartości oczekiwanej: im mniejsza wariancja, tym rozkład 7.L jest bardziej skupiony wokół swej wartości oczekiwanej; im większa wariancja, tym rozkład ZL jest bardziej rozproszony wokół swej wartości oczekiwanej.

Sformułujemy teraz własności wariancji. Ułatwiają one obliczenie wariancji. Ponadto część z nich (własności: VI, V2, V4) pogłębiają nasze zrozumienie wariancji jako miary rozrzutu w artości ZL.